
计算机问题求解一论题3-3 -摊还分析 2020年09月29日
计算机问题求解 – 论题3-3 - 摊还分析 2020年09月29日

问题1:摊还分析有什么用?
问题1:摊还分析有什么用?

特殊的栈操作会带来不可接受的复杂度吗? MULTIPOP(S,k) 1 while not STACK-EMPTY(S)and k >0 2 POP(S) 3 k=k-1 认定push和pop操作都是O(1)时,在一个空栈上执行序列 长度为n的push、pop和Multipop操作,时间复杂度如何? On^2)?
特殊的栈操作会带来不可接受的复杂度吗? 认定push和pop操作都是O(1)时,在一个空栈上执行序列 长度为n的push、pop和Multipop操作,时间复杂度如何? O(n^2)?

最坏情况下,仍然是O()的! ·在一个空栈上的n个操作,不可能出现n个multipop操作! 虽然我们相信不会是O(^2),但是我们仍然要找 到一个科学方法去分析这种情况! Aggregate、Account、Potential
最坏情况下,仍然是O(n)的! • 在一个空栈上的n个操作,不可能出现n个multipop操作! 虽然我们相信不会是O(n^2),但是我们仍然要找 到一个科学方法去分析这种情况! Aggregate、Account、Potential
Aggregate(聚合)分析 ·聚合分析的基本思想: ·从宏观上观察,找到n个操作的最坏时间开销T(n) ·从微观上看,每个操作的均摊(平均”)开销就是T(n)/n 必生的n是 什么“东 这里的最 这里的平 西”的规 坏是什么 均是什么 模? 意思? 意思?
Aggregate(聚合)分析 • 聚合分析的基本思想: • 从宏观上观察,找到n个操作的最坏时间开销T(n) • 从微观上看,每个操作的均摊(“平均”)开销就是T(n)/n 这里的n是 什么“东 西”的规 模? 这里的最 坏是什么 意思? 这里的平 均是什么 意思?

从宏观上看(合计): ·每个元素最多只能被pop一次 ·Pop和multipop中的pop的次数总和,最多和push次数一样多 ·长度为n的操作序列,最多有n个元素被(push、pop)操作 尽管multipop:是Ok的,但是,最坏情况下, 合计的操作代价仍然是O()的!
从宏观上看(合计): • 每个元素最多只能被pop一次 • Pop和multipop中的pop的次数总和,最多和push次数一样多 • 长度为n的操作序列,最多有n个元素被(push、pop)操作 尽管multipop是O(k)的,但是,最坏情况下, 合计的操作代价仍然是O(n)的!

N个increase操作的代价 Counter Total value cost 次位翻转:0(1) 0 00000000 0 1 00000001 2 00 000010 3 3 00 000 4 INCREMENT(A) 00 000100 > 00 0 00 101 8 1i=0 6 0 110 10 > 00 00 11 2 while i A.length and Ai==1 8 0 0 0 01 000 15 9 00 0 01001 16 3 A[]=0 10 00 001010 18 4 i=i+1 000010 9 12 00001100 2 5 if i A.length 13 00001101 23 14 00001110 2 6 A[i]=1 15 0000111 26 16 00010000 31 在A的基础上累加1:⊙(k) 将计数器从0累加到16的实际代价
N个increase操作的代价 在A的基础上累加1: Θ(k) 将计数器从0累加到16的实际代价 一次位翻转:O(1)

将计数器从0累加到n,最坏情况翻转代价? 什么是最坏情况? 计数经历从(2i)-1递进到2i时 从0累加到n,最坏代价: O(kn)?
将计数器从0累加到n,最坏情况翻转代价? 什么是最坏情况? O(kn)? 从0累加到n,最坏代价: 计数经历从(2^i)-1递进到2^i时
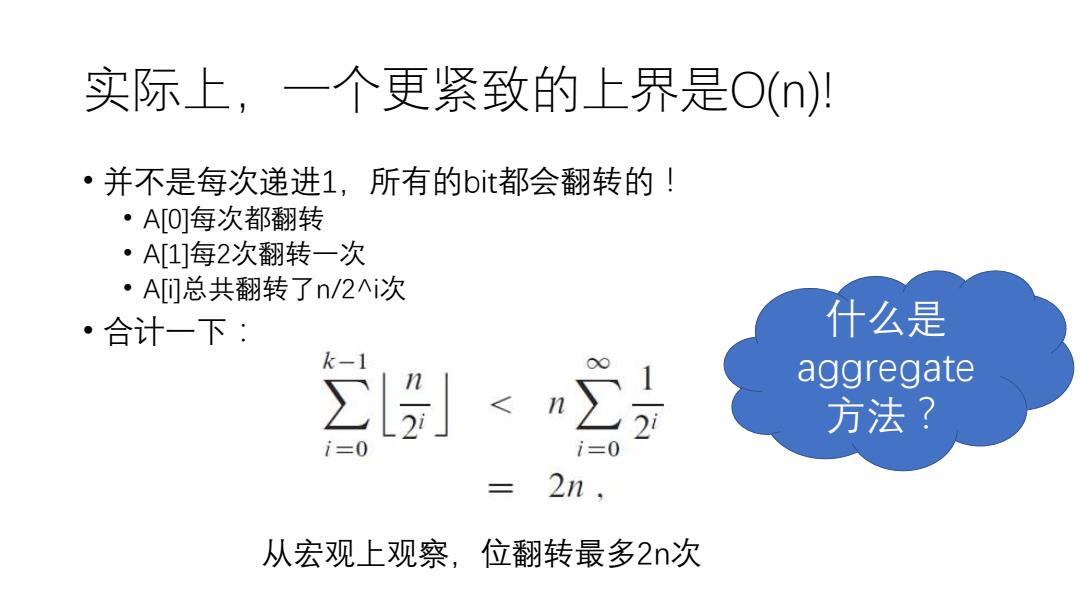
实际上,一个更紧致的上界是O()川 ·并不是每次递进1,所有的bit都会翻转的! ·A[O]每次都翻转 ·A[1]每2次翻转一次 ·A总共翻转了n/2i次 ·合计一下: 什么是 」<n∑ aggregate 方法? i=0 三 2n. 从宏观上观察,位翻转最多2n次
实际上,一个更紧致的上界是O(n)! • 并不是每次递进1,所有的bit都会翻转的! • A[0]每次都翻转 • A[1]每2次翻转一次 • A[i]总共翻转了n/2^i次 • 合计一下: 从宏观上观察,位翻转最多2n次 什么是 aggregate 方法?

核算法accounting ·核算法的基本思想 ·我们不便或者难以全局观测合计代价的前提下,可以从微观出发,考察 每个操作的代价 ·测算每个动作的实际代价 ·赋予(且通过核算不断优化)每个动作的摊还代价 ·核算依据: :≥∑c 如果左式始终 成立,左式的 i=】 左部有何意义? 总摊还代价不断逼近实际代价
核算法accounting • 核算法的基本思想 • 我们不便或者难以全局观测合计代价的前提下,可以从微观出发,考察 每个操作的代价 • 测算每个动作的实际代价 • 赋予(且通过核算不断优化)每个动作的摊还代价 • 核算依据: 总摊还代价不断逼近实际代价 如果左式始终 成立,左式的 左部有何意义?