
计算机问题求解一论题4-2 -置换群与拉格朗日定理 2021年3月3日
计算机问题求解 – 论题4-2 - 置换群与拉格朗日定理 2021年3月3日
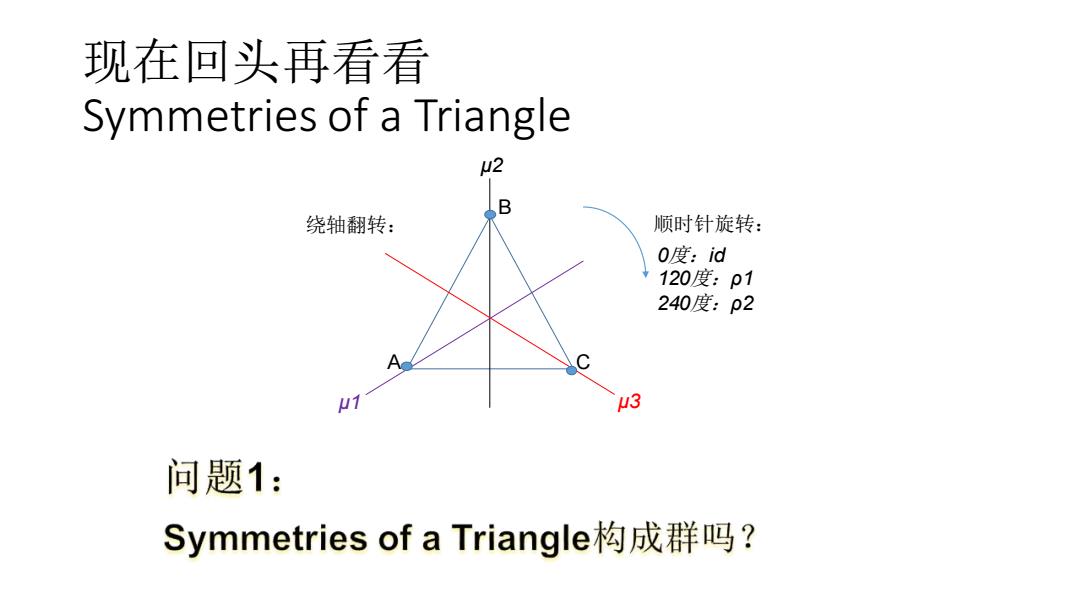
现在回头再看看 Symmetries of a Triangle u2 B 绕轴翻转: 顺时针旋转: 0度:id 120度:p1 240度:p2 1 u3 问题1: Symmetries of a Triangle构成群吗?
现在回头再看看 Symmetries of a Triangle A B C 0度:id 120度:ρ1 240度:ρ2 μ2 μ1 μ3 绕轴翻转: 顺时针旋转:

问题2: 任意非空集合上所有一一对应 的函数及函数复合运算一定能 构成一个群? Sn:n元素对称群 置换群:Sn的子群
Sn:n元素对称群 置换群:Sn的子群

关于置换的轮换表示 2345 6 42356/ =(243) 1g89)=12r66 12 2345
关于置换的轮换表示

置换复合运算示例 It is very easy to compute products of cycles.Suppose that σ=(1352) andT=(256).u=(1634) 0T三? 0L=? 123456 /123456 325461 614325
置换复合运算示例 ? ? 123456 325461 123456 614325

关于轮换的若干结论 Let o and T be two disjoint cycles in Sx.Then oT=To. PROOF.Let o =(a1,a2,...,ak)and T (61,62,...,b).We must show that or(x)=To(x)for all x E X. 破题 技巧: 分情形证明法:分析x在两个轮换中出现的不同情况
关于轮换的若干结论 技巧: 分情形证明法:分析x在两个轮换中出现的不同情况 破题

关于轮换的若干结论 Every permutation in Sn can be written as the product of disjoint cycles. 看这个例子: 2345 6 3 2 1 5 6 4 问题3:如何用数学 我们可以构造出: 语言描述出我们的构 (13)(2)(456) 造过程和结论?
关于轮换的若干结论 看这个例子: 我们可以构造出: (13)(2)(456) 问题3:如何用数学 语言描述出我们的构 造过程和结论?

关于轮换的若干结论 23 456 T= (13)(2)(456) 321564 Define X1 to be {o(1),02(1),...} Define Xi to be {o(i),o2(i),...},where i is the first integer in X but X1 ......let number of Xi be r If o;is the cycle defined by )x∈X xgXi, then o =0102...or.Since the sets X1,X2,...,Xr are disjoint,the cycles 01,02,...,or must also be disjoint. 口
关于轮换的若干结论 (13)(2)(456) Define X1 to be {σ(1), σ 2 (1),…} Define Xi to be {σ(i), σ 2 (i),…},where i is the first integer in X but X1 ……, let number of Xi be r

问题4.1:你能一眼看出这个结论吗? (a1,a2,,an)=(a1an)(a1an-1)…(a1a3)(a1a2) 问题4.2:上述结论如何导致这个命题的? Proposition 5.4 Any permutation of a finite set containing at least two elements can be written as the product of transpositions. 问题5:你能很快地给出一个置换的逆是什么吗?
问题4.1:你能一眼看出这个结论吗? 问题5:你能很快地给出一个置换的逆是什么吗? 问题4.2:上述结论如何导致这个命题的?

副扑克牌,如果洗牌时每次交换两张牌,洗 牌n次后,恰好还原了。请问n有可能是137吗? If the identity is written as the product of r transpositions, id=T1T2…Tr, then r is an even number
一副扑克牌,如果洗牌时每次交换两张牌,洗 牌n次后,恰好还原了。请问n有可能是137吗?