
计算机问题求解-论题2-14 -B树 2020年05月28日
计算机问题求解 – 论题2-14 -B树 2020年05月28日

问题1:我们之前考察一个数据结构的某 个操作的性能时,为什么没有考虑数据读 写的时间开销?
问题1:我们之前考察一个数据结构的某 个操作的性能时,为什么没有考虑数据读 写的时间开销?
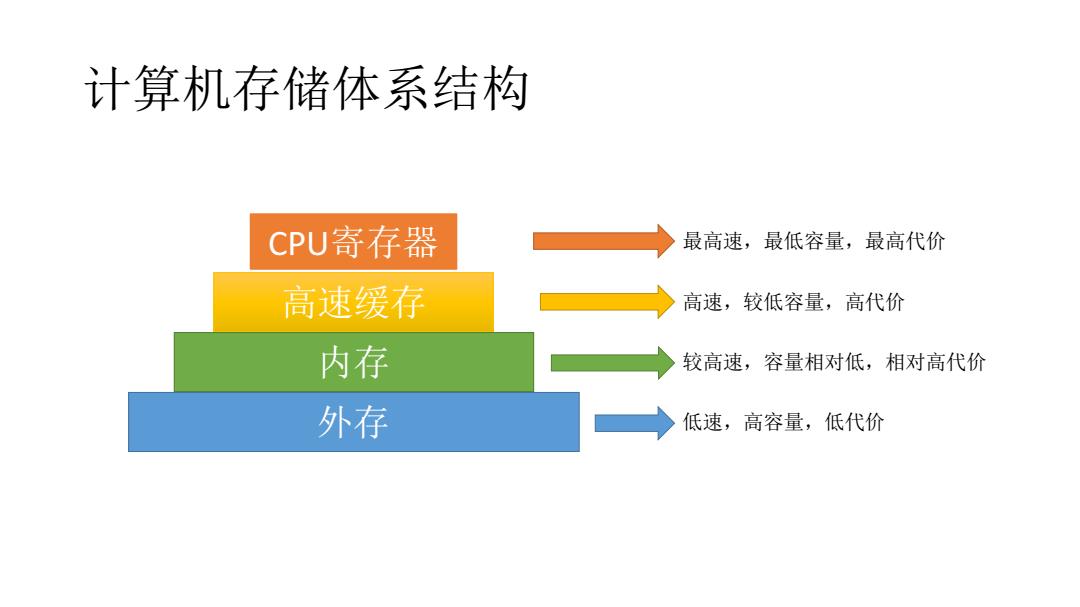
计算机存储体系结构 CPU寄存器 最高速,最低容量,最高代价 高速缓存 高速,较低容量,高代价 内存 较高速,容量相对低,相对高代价 外存 低速,高容量,低代价
计算机存储体系结构 CPU寄存器 高速缓存 内存 外存 最高速,最低容量,最高代价 高速,较低容量,高代价 较高速,容量相对低,相对高代价 低速,高容量,低代价
实际上: ·当处理很大的文件(或者难以将所有数据都一次性载入内存再计 算)时,我们总是根据需要从外存读取数据进入内存,总是从内 存中将更新的数据写到外存 写出 读入
实际上: • 当处理很大的文件(或者难以将所有数据都一次性载入内存再计 算)时,我们总是根据需要从外存读取数据进入内存,总是从内 存中将更新的数据写到外存 写出 读入

look separately at the two principal components of the running time: the number of disk accesses,and the CPU(computing)time. 15 6 18 spindle platter track read/write head 当我们受限于(受惠于) 现实的物理世界时,我们 该如何思考? arms
磁盘访问机理 当我们受限于(受惠于) 现实的物理世界时,我们 该如何思考?

问题3: 假定我们需要存储10亿个键值。检索是作 用在该数据集上的重要操作。请问,你该 如何为此类应用设计外存上的数据结构? 你能想到的最好的数据结构是什么?
问题3: 假定我们需要存储10亿个键值。检索是作 用在该数据集上的重要操作。请问,你该 如何为此类应用设计外存上的数据结构? 你能想到的最好的数据结构是什么?
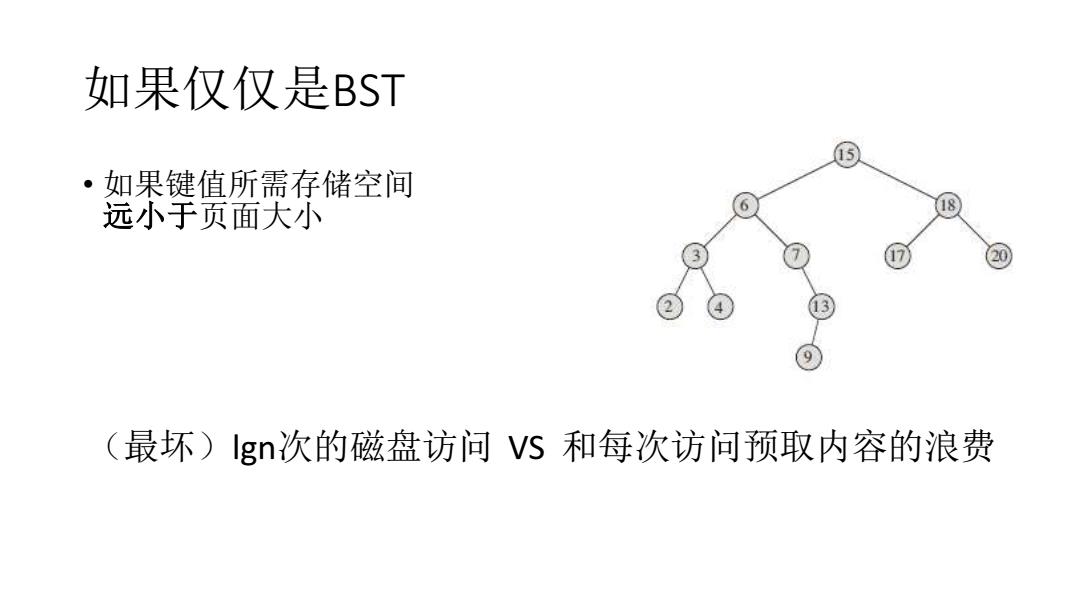
如果仅仅是BST ·如果键值所需存储空间 远小于页面大小 18 (最坏)gn次的磁盘访问VS和每次访问预取内容的浪费
如果仅仅是BST • 如果键值所需存储空间 远小于页面大小 (最坏)lgn次的磁盘访问 VS 和每次访问预取内容的浪费
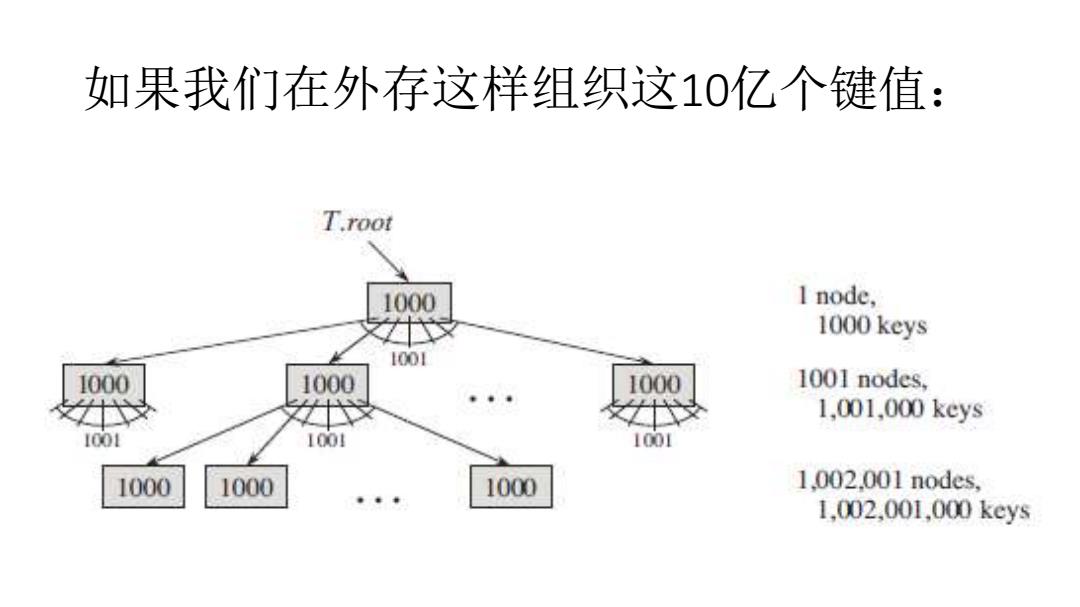
如果我们在外存这样组织这10亿个键值: T.root 1000 I node, 1000 keys 1001 1000 1000 1000 1001 nodes, 1.001.000kcys 1001 1001 1001 1000 1000 1000 1.002.001 nodes,. 1,002.001,000kcys
如果我们在外存这样组织这10亿个键值:
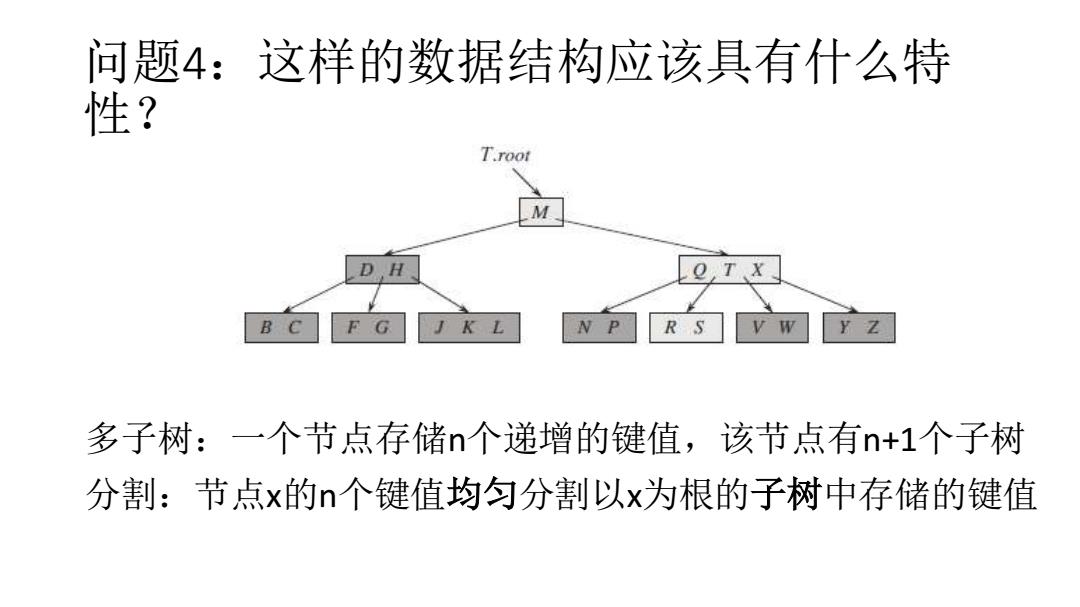
问题4:这样的数据结构应该具有什么特 性? T.root T NP Y Z 多子树:一个节点存储n个递增的键值,该节点有n+1个子树 分割:节点x的个键值均匀分割以x为根的子树中存储的键值
问题4:这样的数据结构应该具有什么特 性? 多子树:一个节点存储n个递增的键值,该节点有n+1个子树 分割:节点x的n个键值均匀分割以x为根的子树中存储的键值

B-树的性质 1.Every node x has the following attributes: a.x.n,the number of keys currently stored in nodex, b.the x.n keys themselves,x.key,x.key2,....x.keyx.n,stored in nondecreas- ing order,so thatx.key1≤x.key2≤…≤x.keyx.m c.x.leaf,a boolean value that is TRUE if x is a leaf and FALSE if x is an internal node. 2.Each internal node x also contains x.n+1 pointers x.c1,x.c2,....x.Cx.n+1 to its children.Leaf nodes have no children,and so their ci attributes are unde- fined. 3.The keys x.key;separate the ranges of keys stored in each subtree:if ki is any key stored in the subtree with root x.ci,then k1≤x.key1≤k2≤x.key2≤…≤x.keyx.n≤kx.n+1·
B-树的性质