
计算机问题求解一论题4.10 优化问题的近似解 陶先平 2019年5月22日
计算机问题求解—论题4.10 优化问题的近似解 陶先平 2019年5月22日

近似算法为什么有用? "If an optimization problem does not admit any efficient algorithm computing an optimal solution,is there a possibility to efficiently com- pute at least an approzimation of the optimal solution?" •牺牲可以容忍的一点点误差 ·得到一个可实运行的求解斧生 何谓一点点? 何谓误差?
近似算法为什么有用? •牺牲可以容忍的一点点误差 •得到一个可现实运行的求解算法 何谓一点点? 何谓误差?

近似算法的若干基本概念 an approximation algorithm for an optimization problem is an algorithm that provides a feasible solution whose quality does not differ too much from the quality of an optimal solution. 这段文字中的quality是什么意思? 这个公式中的cost是什么意思? 针对实例x EA(x)= cost(A(x))-Optu(xr川 的相对误差 Optu()
这个公式中的cost是什么意思? 近似算法的若干基本概念 这段文字中的quality是什么意思? 针对实例x 的相对误差

近似算法的若干基本概念 For any n e N,we define the relative error of A as 问题规模为n时 eA(n)=max{EA(x)lx∈Lr∩(∑r)"}. 算法级别 上的误差 到底定义了什么误 差?
到底定义了什么误 差? 问题规模为n时 算法级别 上的误差 近似算法的若干基本概念

近似算法的若干基本概念 For every xe LI,the approximation ratio Ra(x)of A on x is defined as ∫cost(A(x)Optu(c)) RA()=max Optu()cost(A() For any n E N,we define the approximation ratio of A as RA(n)=max {RA(x)ELI(I)
近似算法的若干基本概念

我们希望能够得到某个近似算法的如下结论: For any positive real 6 1,we say that A is a 6-approximation algo- rithm for U if RA(z)≤6 for every x∈Lr: 如果不能,我们要努力得到某个近似算法的这个结论: For every function f:NN-R,we say that A is an f(n)-approximation algorithm for U if RA(n)≤f(n)for every n∈N
我们希望能够得到某个近似算法的如下结论: 如果不能,我们要努力得到某个近似算法的这个结论:

如何评价一个近似算法的“好坏” 1,针对某个特定的问题输入,A的解和最优解的误差 在不知道最优解的情况下,如何评估? 2,针对某个规模的各种问题输入,A的最大误差; 3,针对问题的所有可能输入,A的误差变化趋势: 将所有输入可能,建模为n的增长 4,给出一个误差的界限,证明A近似算法的误差的界限 绝对的某个值,或者某个函数
如何评价一个近似算法的“好坏” 1,针对某个特定的问题输入,A的解和最优解的误差 在不知道最优解的情况下,如何评估? 2,针对某个规模的各种问题输入,A的最大误差; 3,针对问题的所有可能输入,A的误差变化趋势: 将所有输入可能,建模为n的增长 4,给出一个误差的界限,证明A近似算法的误差的界限 绝对的某个值,或者某个函数
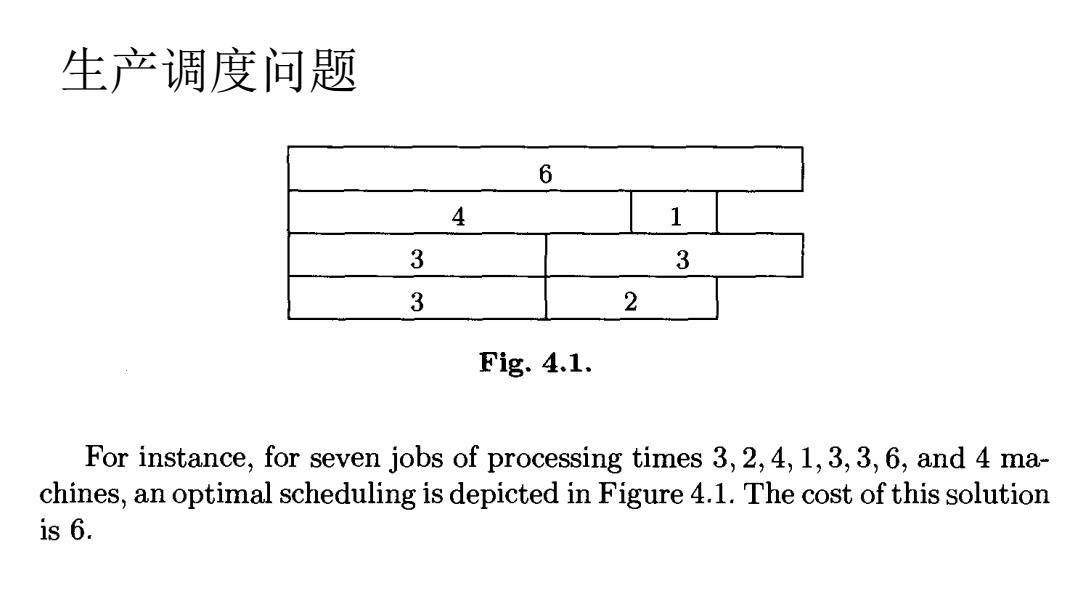
生产调度问题 6 4 1 3 3 3 2 Fig.4.1. For instance,for seven jobs of processing times 3,2,4,1,3,3,6,and 4 ma- chines,an optimal scheduling is depicted in Figure 4.1.The cost of this solution s6
生产调度问题

生产调度问题的一个近似解 Algorithm 4.2.1.3 (GMS (GREEDY MAKESPAN SCHEDULE)). Input:I=(p1,...,Pn,m),n,m,p1,...,Pn positive integers and m 2. Step 1:Sort p1,...,Pn. To simplify the notation we assume p1≥p2≥·≥pn in the rest of the algorithm. Step 2:for i=1 to m do begin Ta:={i); Time(Ti):=pi end In the initialization step the m largest jobs are distributed to the m machines.At the end,Ti should contain the indices of all jobs assigned to the ith machine for i=1,...,m.} Step 3:for i=m+1 to n do begin compute an I such that Time(T)=min{Time(Til≤j≤m; T:=TUfi: Time(Ti):=Time(Ti)+pi end Output:(Ti,T2,...,Tm)
生产调度问题的一个近似解
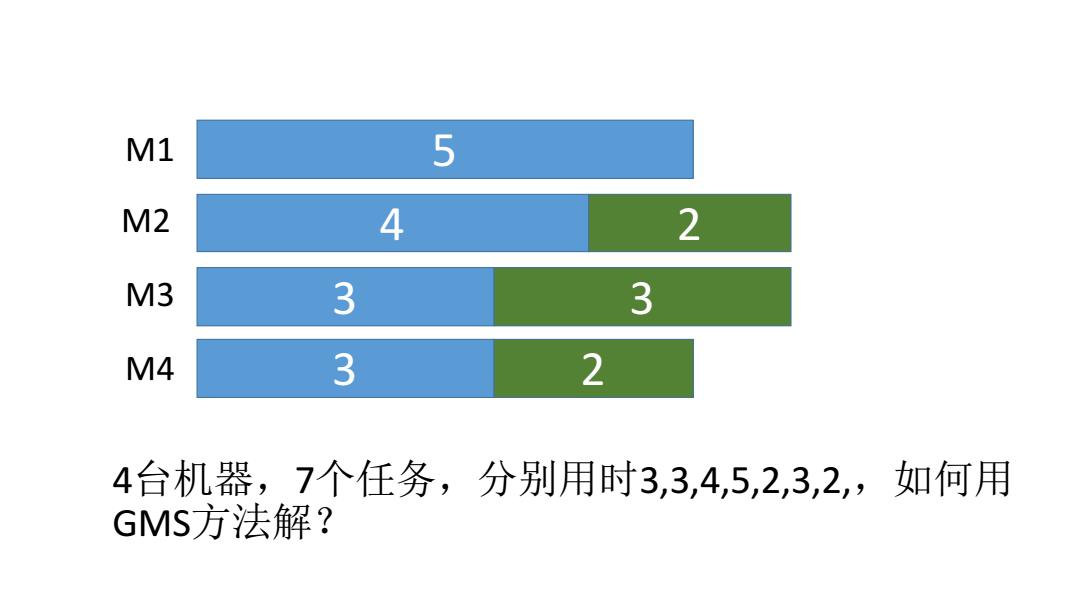
M1 5 M2 4 2 M3 3 3 M4 3 2 4台机器,7个任务,分别用时3,3,4,5,2,3,2,如何用 GMS方法解?
4台机器,7个任务,分别用时3,3,4,5,2,3,2,,如何用 GMS方法解? M1 M2 M3 M4 5 4 3 3 3 2 2