
计算机问题求解 -论题2-14 树及搜索树 2016年05月26日
计算机问题求解 – 论题2-14 - 树及搜索树 2016年05月26日
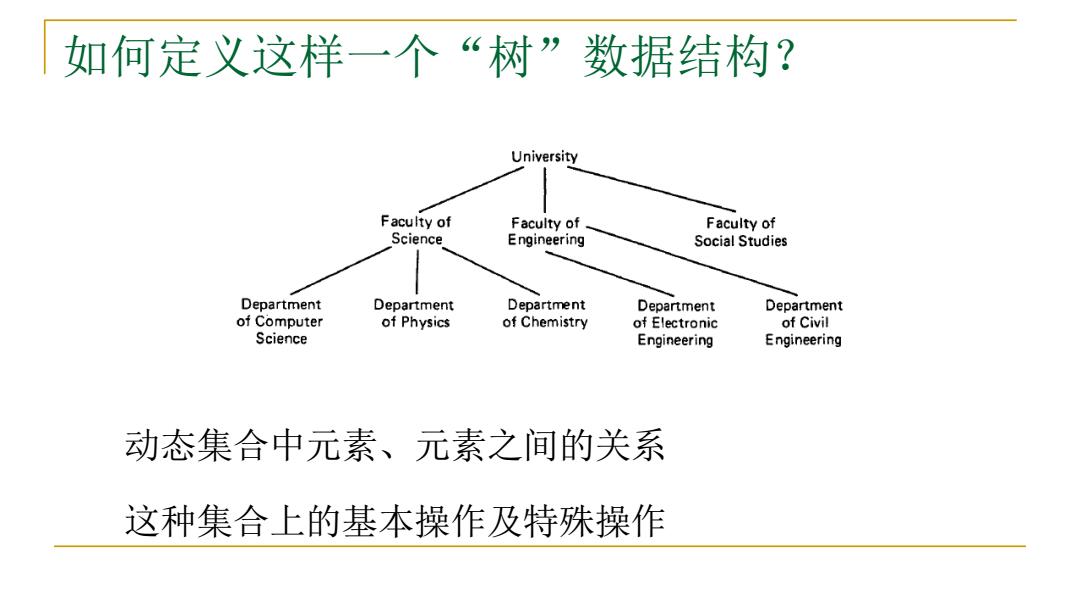
如何定义这样一个“树”数据结构? University Faculty of Faculty of Faculty of Science Engineering Social Studies Department Department Department Department Department of Computer of Physics of Chemistry of Electronic of Civil Science Engineering Engineering 动态集合中元素、元素之间的关系 这种集合上的基本操作及特殊操作
如何定义这样一个“树”数据结构? 动态集合中元素、元素之间的关系 这种集合上的基本操作及特殊操作

树中元素及元素之间的关系 A tree is a recursive abstract data type which is a collection of zero or more nodes each containing an element of type elemtype with the following hierarchi- cal structure: either (a)The empty structure(with no nodes) or (b)A node N containing element E with a finite number (zero or more)of associated disjoint tree structures (that is,they have no common nodes).These trees are known as subtrees of N.N is called the root of the tree. 你如何理解这两个概念:层次结构、递归ADT?
树中元素及元素之间的关系 你如何理解这两个概念:层次结构、递归ADT?

树中元素上应该有哪些操作?基本操作B)?特 殊操作(S)? B B S B S
树中元素上应该有哪些操作?基本操作(B)?特 殊操作(S)? B B B S S

function left_most_child (N node):node; (This function returns the left-most child of the node N. S If there are no children,a null node will be returned * function right_sibling (N:node):node; (If node N has a sibling node,it will be retured as the value of this S function.Otherwise,a null node will be returned * function null_node (N:node):boolean; (This function returns a true value if and only if N is a null node * B/S function cons_treen (E:elemtype;T1,T2,...,Tn:tree):tree; (This function constructs a tree with a node N as its root containing element E and the trees T1,T2,...,Tn as its children,in that order. B/S The trees T1,T2,...,Tn should not be used again after this operation to construct other trees.If copies of these subtrees are required,they can be constructed using the assign(T,T)operation.This is meant for space-efficiency so that this function need not copy these subtrees in order to make a new tree *
S S B/S B/S

procedure insert_child (P:node;E:elemtype); (This procedure is defined for constructing trees in a top-down manner. B A node containing element E will be created and it will be made the right-most child of node P*) procedure delete (var T:tree); B (This procedure deletes all the nodes of the tree T,and T will be made an empty tree.The tree T should not be a subtree of another tree * procedure assign(T1 tree;var T2:tree); (This procedure copies the entire tree T1 and asigns it to T2 * S/B 你能够从你的判断中得到一个一般 性的规律吗: 当你定义一个数据结构时,哪些操 作是必须的,哪些操作是特定的?
B B S/B 你能够从你的判断中得到一个一般 性的规律吗: 当你定义一个数据结构时,哪些操 作是必须的,哪些操作是特定的?

你有没有感觉到,在树这样的数据结构中,递 归如呼吸般自然? ways.These are known as tree walkings or tree traversals.In a tree with the root N and subtrees T1,T2,...,Tn we define: pre-order traversal:visit the root node N,then visit all the nodes in T in pre-order,then visit all the nodes in T2 in pre-order, and so on until all the nodes in Tn are visited in pre-order. post-order traversal:visit the nodes of T1,T2,...,Tn in post-order (in that order);then visit the root node
你有没有感觉到,在树这样的数据结构中,递 归如呼吸般自然?
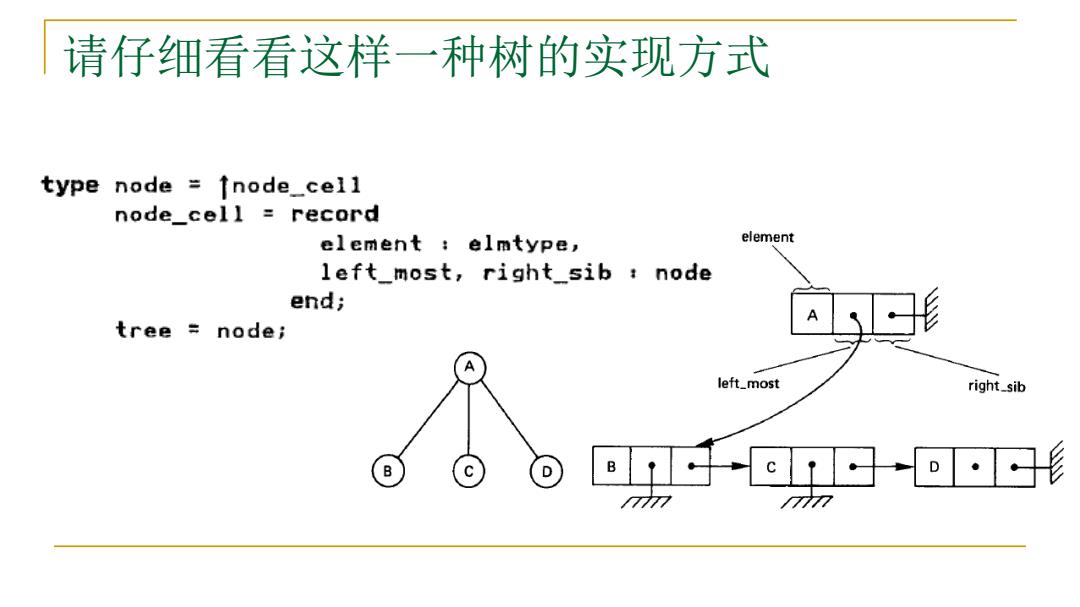
请仔细看看这样一种树的实现方式 type node÷1node_cei1 node_cel】=record element elmtype, element left_most,right_sib node end; tree node; □形 A left_most right_sib B ©□-o形 7777 777
请仔细看看这样一种树的实现方式
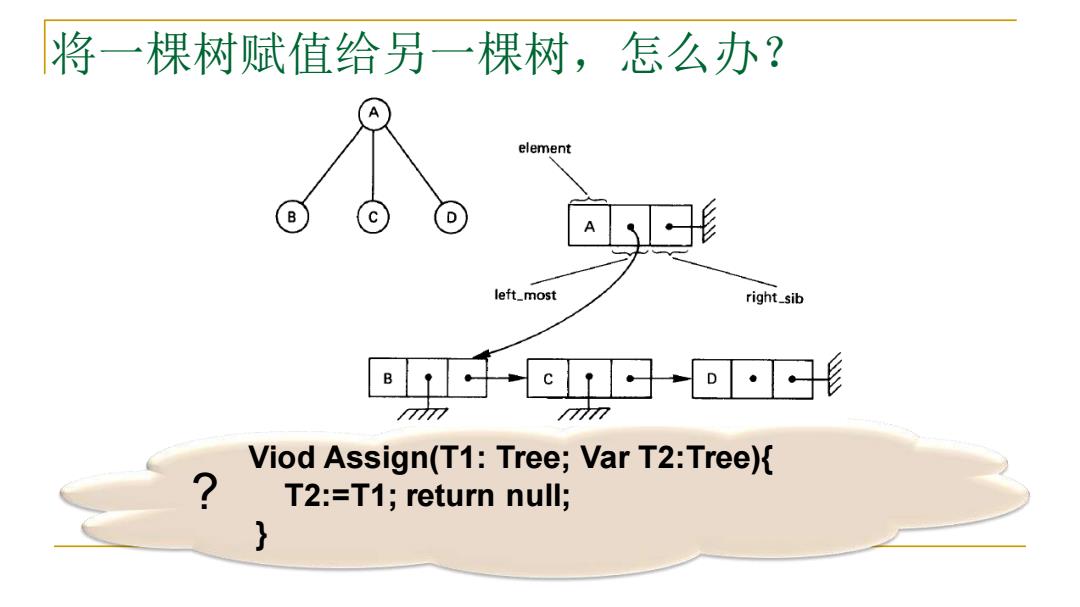
将一棵树赋值给另一棵树,怎么办? element D 5形 left_most right_sib 中©1→o·囚形 777 777 Viod Assign(T1:Tree;Var T2:Tree){ T2:=T1;return null; }
将一棵树赋值给另一棵树,怎么办? Viod Assign(T1: Tree; Var T2:Tree){ T2:=T1; return null; } ?
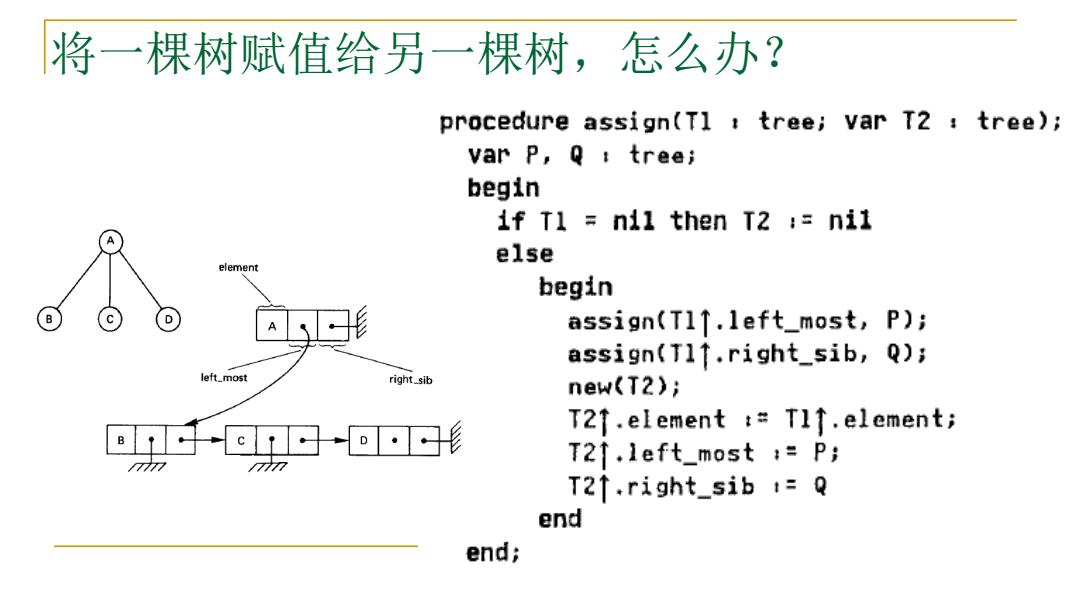
将一棵树赋值给另一棵树,怎么办? procedure assign(T1 tree;var T2 tree); var P,Q tree; begin if T1 nil then T2 :ni1 else element begin 形 assign(T11.left_most,P); assign(Tl1.right_sib,Q); left_most right_sib new(T2); T21.element :Tlf.element; c-o·形 T21.left_most :P; T21.right_sib =Q end end;
将一棵树赋值给另一棵树,怎么办?