
计算机问题求解一论题2-10 排序与选择 2018年05月02日
计算机问题求解 – 论题2-10 - 排序与选择 2018年05月02日

问题1: 你能否利用下图解释快速排 序的基本思想? [first灲 [splitPoint]:pivot [last] 0000O0100000000 for any element in this for any element in this segment,the key small large segment,the key is not less than pivot. is less than pivot. To be sorted recursively
[first] [last] for any element in this segment, the key is less than pivot. for any element in this segment, the key is not less than pivot

QUICKSORT(A,p.r) 1 if p<r 2 g PARTITION(A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A,g+1.r) To sort an entire array A,the initial call is QUICKSORT(A,1.A.length) 问题2: 都是用divide-and conquer策略,这与 Mergesort?有什么不同?
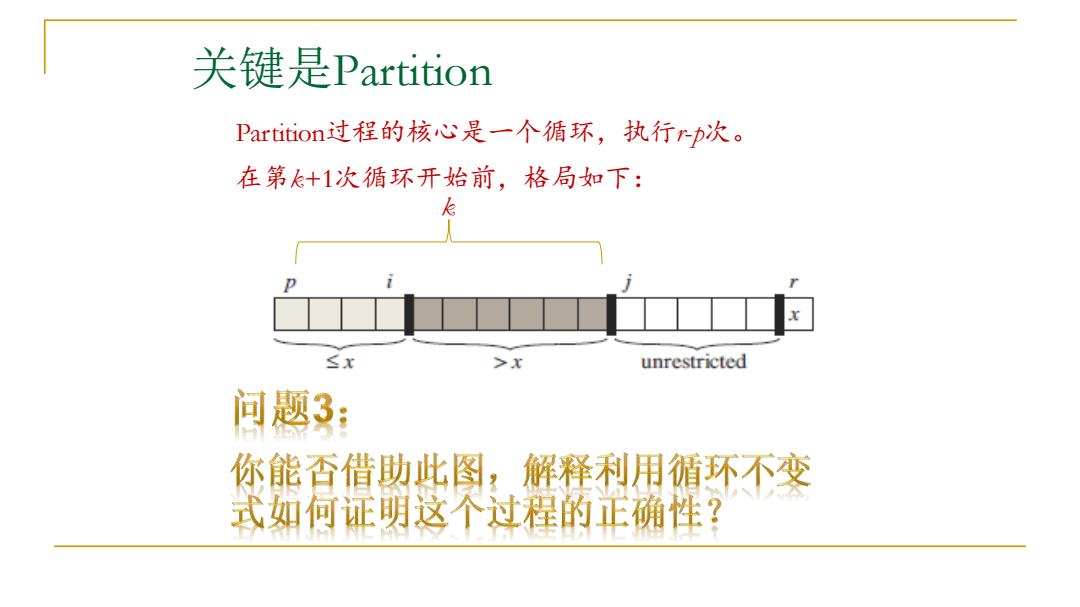
关键是Partition Partition过程的核心是一个循环,执行rp次。 在第+1次循环开始前,格局如下: k ≤x >x unrestricted 问题3: 你能否借助此图,解释利用循环不变 式如何证明这个过程的正确性?
关键是Partition Partition过程的核心是一个循环,执行r-p次。 在第k+1次循环开始前,格局如下: k

QUICKSORT(A,p.r) 1 if p<r 2 g PARTITION(A,p,r) 3 QUICKSORT(A,p,q-1) 4 QUICKSORT(A.g+1.r) To sort an entire array A,the initial call is QUICKSORT(A,1.A.length) 问题4: 这个递归算法的时间性能递归式是什么?
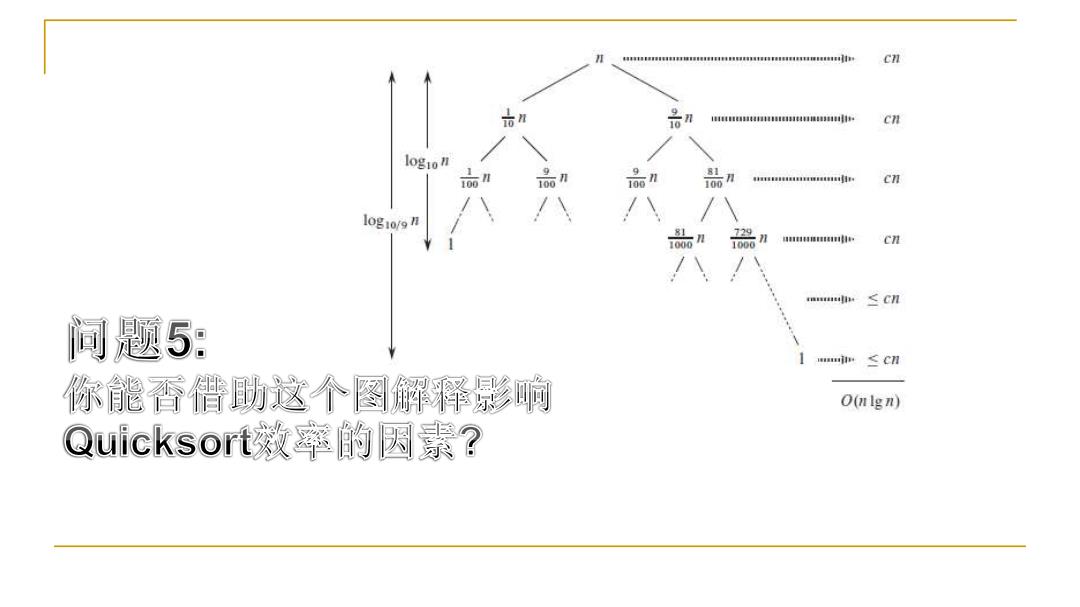
和球有料精有有转码博打中 C刀 品n cn logion 品和 4程h cn log10/9 n 品n 器n C拉 a≤Cn 间题5: ≤C 你能香借助这个图解释影响 O(nlgn) Quicksort效率的因素?

In fact,any split of cont proportioality yiedsr of ept)where thecsta level is O().The rnning time is therefore ()whenever the split has constant rorionity. 问题⑥; 你看了这句话有什么想法?

问题7 为什么直观上也会觉得快速排序的平均效 率更接近最好情况,而不是最坏情况? 直觉对于探索很重要。 “大胆假设,小心求证!” EE1A1EEB1111 Θ(n) A811211801118888i Θ(n) 0 2- (n-1)/2 (n-1)/2 (n-1)/2-1 (n-1)/2 (a) (b)
直觉对于探索很重要。 “大胆假设,小心求证!

Worst-Case Performance of Quicksort T(n)=max (T(q)+T(n-q-1))+(n) 0≤g≤n-1 g是Partition的返回值。 问题8: 你能说说解这个递 归的策略吗? Guess and verifying
Worst-Case Performance of Quicksort q是Partition的返回值。 Guess and verifying

再次观察partition过程 PARTITION(A,p,r) 1 x=A[r] 2i=p-1 3 for j=ptor-1 4 ifA[j]≤x 5 i=i+1 6 exchange A[i]with A[j] 7 exchange A[i+1]with A[r] 8 return i +1
再次观察partition过程