
面向问题求解的学习和实 践 陶先平 南京大学计算机科学与技术系
面向问题求解的学习和实 践 陶先平 南京大学计算机科学与技术系

日录 ·为什么我们命名这个两年的课程是“问题求解” ·我们学习过哪些问题求解的基本知识? ·我们的问题求解能力训练到底如何?
目录 • 为什么我们命名这个两年的课程是“问题求解” • 我们学习过哪些问题求解的基本知识? • 我们的问题求解能力训练到底如何?
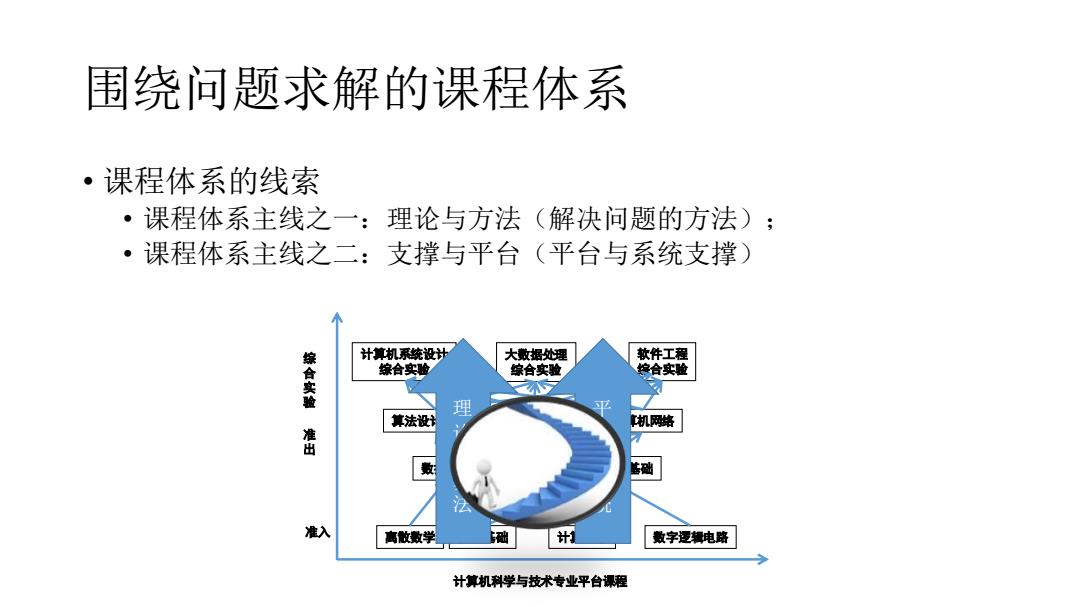
围绕问题求解的课程体系 ·课程体系的线索 ·课程体系主线之一:理论与方法 (解决问题的方法); ·课程体系主线之二:支撑与平台(平台与系统支撑) 计算机系统设计 大数据处理 软件工程 综合实验 综合实验 综合实验 综合实验 理 算法设: 机网路 数 准入 离散数学 础 计 数字逻辑电路 计算机科学与技术专业平台课程
围绕问题求解的课程体系 • 课程体系的线索 • 课程体系主线之一:理论与方法(解决问题的方法); • 课程体系主线之二:支撑与平台(平台与系统支撑) 准入 离散数学 程序基础 计算思维 数字逻辑电路 准 出 数据结构 算法设计与分析 计算机系统基础 操作系统 计算机网络 计算机科学与技术专业平台课程 计算机系统设计 综合实验 大数据处理 综合实验 软件工程 综合实验 综 合 实 验 理 论 与 算 法 平 台 与 系 统

“问题的求解”能力是什么? 。什么叫“问题的求解”? ·解问题的基本方法 理解问题 ·Polya的Problem solving:基本方法 ·如何理解问题和制定计划 ·问题的形式化 制定计划 ·模糊问题的数学描述 ·基础理论 ·数学模型 计划执行 ·算法的设计、分析及优化 ·含设计策略、正确性证明 ·数据结构的设计及算法的实现 回顾检查 ·程序设计及优化
“问题的求解”能力是什么? • 什么叫“问题的求解”? • 解问题的基本方法 • Polya的Problem solving基本方法 • 如何理解问题和制定计划 • 问题的形式化 • 模糊问题的数学描述 • 基础理论 • 数学模型 • 算法的设计、分析及优化 • 含设计策略、正确性证明 • 数据结构的设计及算法的实现 • 程序设计及优化 理解问题 制定计划 计划执行 回顾检查
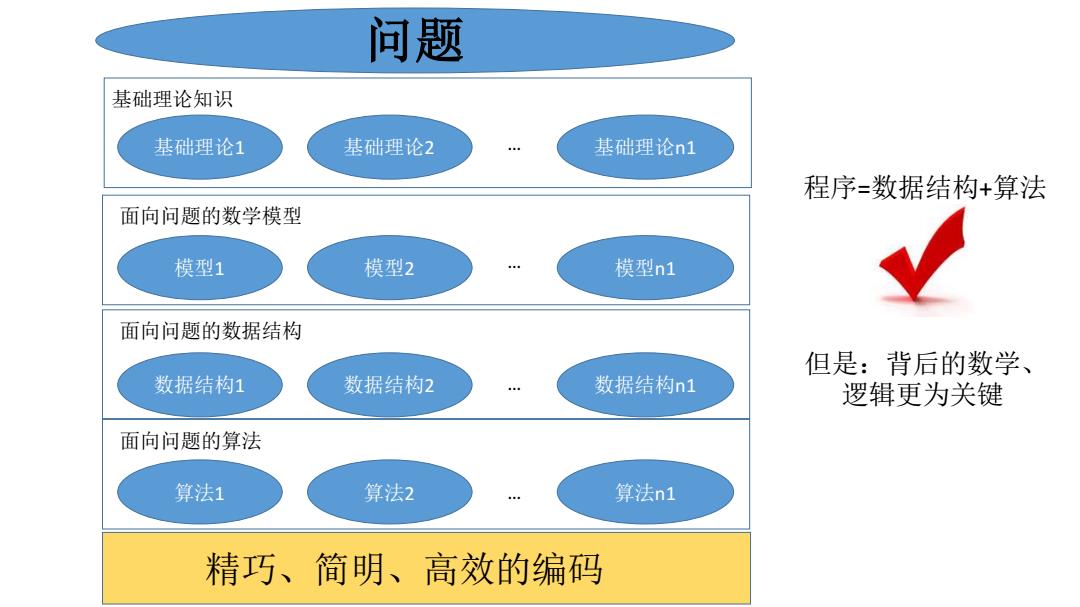
问题 基础理论知识 基础理论1 基础理论2 基础理论n1 程序=数据结构+算法 面向问题的数学模型 模型1 模型2 模型n1 面向问题的数据结构 但是:背后的数学、 数据结构1 数据结构2 数据结构nl 逻辑更为关键 面向问题的算法 算法1 算法2 算法n1 精巧、简明、高效的编码
问题 基础理论1 基础理论2 基础理论n1 基础理论知识 模型1 模型2 模型n1 面向问题的数学模型 精巧、简明、高效的编码 … … 算法1 算法2 算法n1 面向问题的算法 … 数据结构1 数据结构2 数据结构n1 面向问题的数据结构 … 程序=数据结构+算法 但是:背后的数学、 逻辑更为关键

传统的课程体系存在的不足在于 ·知识点及其应用在时序上有错位 ·程序设计课程总是难以定位 ·复杂程序难度太大,toy级程序实在无趣 ·知识点及其应用在时序上被脱节 ·书到用时已忘了 ·数理逻辑中的命题符号化、数学归纳法和循环不变式 ·概率论和算法时间渐进复杂度分析 ●… ·知识点及其应用在安排上各自为营,效率低下 ·课程之间边界模糊,教学目标不明确 ·重复太多,缺失不知
传统的课程体系存在的不足在于 • 知识点及其应用在时序上有错位 • 程序设计课程总是难以定位 • 复杂程序难度太大,toy级程序实在无趣 • 知识点及其应用在时序上被脱节 • 书到用时已忘了 • 数理逻辑中的命题符号化、数学归纳法和循环不变式 • 概率论和算法时间渐进复杂度分析 • …… • 知识点及其应用在安排上各自为营,效率低下 • 课程之间边界模糊,教学目标不明确 • 重复太多,缺失不知

我们的答案是: ·重构知识体系: ·尽量围绕具体问题,从理论到模型到算法到实现开展组织和学习 ·消除重复,避免遗漏 ·强化应用训练,知识点学习中始终贯穿应用场景 ·在解问题中,不断运用以前学过的知识点 ·以程序设计能力培养为贯穿全课程的基础目标 ·将程序语言及编程的训练隐藏到课堂讲解(引导环节)的”背面” ·穿插在各个课堂讲授中 ·自学、自练 •将自学能力培养放到足够的高度
我们的答案是: • 重构知识体系: • 尽量围绕具体问题,从理论到模型到算法到实现开展组织和学习 • 消除重复,避免遗漏 • 强化应用训练,知识点学习中始终贯穿应用场景 • 在解问题中,不断运用以前学过的知识点 • 以程序设计能力培养为贯穿全课程的基础目标 • 将程序语言及编程的训练隐藏到课堂讲解(引导环节)的”背面” • 穿插在各个课堂讲授中 • 自学、自练 • 将自学能力培养放到足够的高度
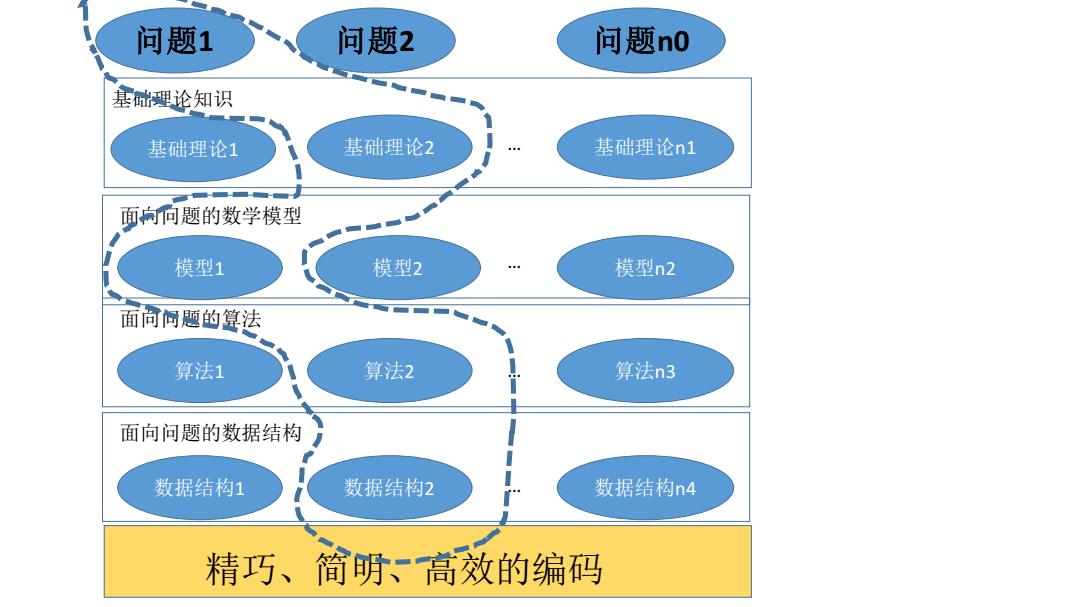
问题1 问题2 问题n0 基础理论知识 基础理论1 基础理论2 基础理论n1 面向向题的数学模型 模型1 模型2 模型n2 面向阿题的篡法 算法1 算法2 算法n3 面向问题的数据结构 数据结构1 数据结构2 数据结构n4 精巧、简明、高效的编码
问题1 基础理论1 基础理论2 基础理论n1 算法1 算法2 算法n3 基础理论知识 面向问题的算法 模型1 模型2 模型n2 面向问题的数学模型 数据结构1 数据结构2 数据结构n4 精巧、简明、高效的编码 面向问题的数据结构 … … … … 问题2 问题n0

形成全新的课程内容体系 ·整个课程内容不是按照传统数学与计算机类课程各自的横向体系划分, 而是围绕问题求解组织成四个“论域”: ·第一个论域“计算入门与数学证明”安排在1年级上学期: ·第二个论域“经典数据结构与算法”安排在1年级下学期; ·第三个论域“典型应用问题及其求解方法”安排在2年级上学期; ·第四个论域“复杂性理论初步与‘难’问题的算法”安排在2年级下学期。 ·上述内容涵盖了传统基础课程:程序设计、离散数学、数据结构、算法设计与 分析 ·希望新体系带来的好处: ·学以致用,缓解“学这些东西有啥用”的焦虑; ·压缩冗余,接触更多的内容; ·学会学习,开启终身学习模式
形成全新的课程内容体系 • 整个课程内容不是按照传统数学与计算机类课程各自的横向体系划分, 而是围绕问题求解组织成四个“论域”: • 第一个论域“计算入门与数学证明”安排在1年级上学期; • 第二个论域“经典数据结构与算法”安排在1年级下学期; • 第三个论域“典型应用问题及其求解方法”安排在2年级上学期; • 第四个论域“复杂性理论初步与‘难’问题的算法”安排在2年级下学期。 • 上述内容涵盖了传统基础课程:程序设计、离散数学、数据结构、算法设计与 分析 • 希望新体系带来的好处: • 学以致用,缓解“学这些东西有啥用”的焦虑; • 压缩冗余,接触更多的内容; • 学会学习,开启终身学习模式

四个论域 ·论域1:计算入门与数学证明 ·帮助学生理解计算思维最核心的概念,接受基本的形式化训练,掌握抽象数学证明的 基本方法。 ·论域2:经典数据结构与算法 ·帮助学生理解抽象数据类型,理解并应用常用的数据结构 ·掌握重要的算法设计策略以及算法设计与分析的基本理论与方法 ·理解并能够应用支持上述内容的离散数学工具与方法。 ·论域3:典型应用问题及其求解方法 ·引导学生掌握典型应用中抽象出来的重要算法问题的求解方法,理解并能够应用支持 上述内容的离散数学工具与方法。 ·论域4:复杂性理论基础与“难”问题的算法 ·涵盖问题求解中复杂性理论的基本内容与问题规约方法,解决“难”问题的主要方法、 技术以及相关的重要理论结果
四个论域 • 论域1:计算入门与数学证明 • 帮助学生理解计算思维最核心的概念,接受基本的形式化训练,掌握抽象数学证明的 基本方法。 • 论域2:经典数据结构与算法 • 帮助学生理解抽象数据类型,理解并应用常用的数据结构 • 掌握重要的算法设计策略以及算法设计与分析的基本理论与方法 • 理解并能够应用支持上述内容的离散数学工具与方法。 • 论域3:典型应用问题及其求解方法 • 引导学生掌握典型应用中抽象出来的重要算法问题的求解方法,理解并能够应用支持 上述内容的离散数学工具与方法。 • 论域4:复杂性理论基础与“难”问题的算法 • 涵盖问题求解中复杂性理论的基本内容与问题规约方法,解决“难”问题的主要方法、 技术以及相关的重要理论结果