
计算机问题求解一论题3-9 All-Pair Shortest Paths 2016年11月2日
计算机问题求解 – 论题3-9 - All-Pair Shortest Paths 2016年11月2日

复习 ■动态规划的解题基本规律是什么? 口最优子结构分析 口递归定义最优解 口设计自底向上算法依次求解
复习 动态规划的解题基本规律是什么? 最优子结构分析 递归定义最优解 设计自底向上算法依次求解
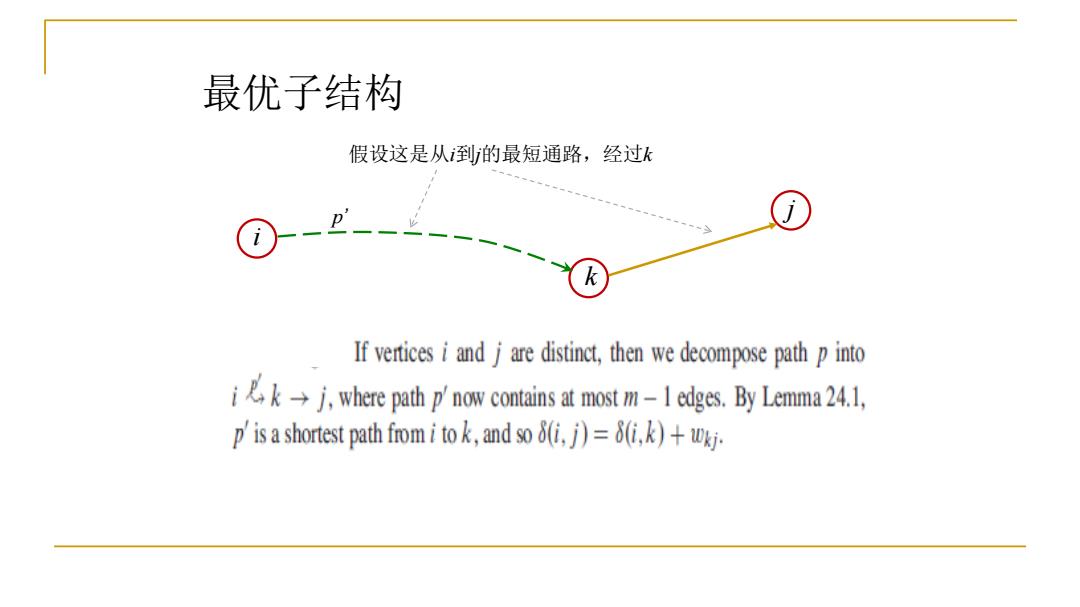
最优子结构 假设这是从到的最短通路,经过k If vertices i andare distinct,then we decompose path p into iwhere path pnow contains at most m-l edges.By Lemma 24.1. p'is a shortest path fromitok,ands)=(ik)j
i k j 假设这是从i到j的最短通路,经过k p ’ 最优子结构

递归定义最优解 Now,letbe the minimum weight of any path from vertexito vertexjthat contains at most m edges.When m =0,there is a shortest path from i to j with no edges if and only if i =j.Thus, 98 ifi=j, fi卡j. For mwe computeas the minimum of(the weight of a shortest path from i to j consisting of at most m-I edges)and the minimum weight of any path from i to j consisting of at most m edges,obtained by looking at all possible predecessors k of j.Thus,we recursively define min (份”mng+0) 1<k< min +w (25.2) 1<k≤别 The latter equality follows since w=0for all j
递归定义最优解

问题1: 作:行10个的,的i观义是什么? 如果=7,能认节点间的最短路径长度 是7吗?

问题2: 为什么8,)=-”?

问题3: 如果定义矩阵L=(),L1,L2, .,L”-1分别表示什么含义? 如何去计算L

自底向上计算 The heart of the algorithm is the following procedure,which,given matrices L()and W,returns the matrix L(m).That is,it extends the shortest paths com- puted so far by one more edge. EXTEND-SHORTEST-PATHS(L,W) 1 n L.rows 2 let L'= (be a new nx nmatrix 问题4: 3 for i=1 to n 4 for j 1to n 5 号=∞ one more 6 for k 1to n 7 号=min(5,lk+0对) edge”体现在 8 return L' 哪里?
自底向上计算

只需要扩展n-2次 SLOW-ALL-PAIRS-SHORTEST-PATHS(W) 1 n W.rows 2L0=W 3 for m 2to n-1 2 4 let L m)be a new nmatrix 5 L)=EXTEND-SHORTEST-PATHS(L-W) 6 return L(-1) 6 3 8 4 0 2 0 L() 0 1 7 L2= 3 40 304- 84051 471 2 2 00 06 0 506
只需要扩展n-2次

问题5: 为什么上述算法被称为“慢” 算法,为什么它可能被加快?