
计算机问题求解一论题2-1 。算法方法 2015年2月25日
计算机问题求解 – 论题2-1 - 算法方法 2015年2月25日

问题1: 你能解释下面的话吗? It is all very well talking about the constructs that an algorithm may use-that is,the pieces it might be composed of-but we must say something more about the ways of going about using these pieces to make a whole

搜索“解空间”一一个例子 ■一位父亲请一位数学家猜他3个孩子的年龄,他提示说: 口3人年龄的乘积是36。 口这时他们恰好经过一幢房子,父亲又提示说:他们年龄之和等于这房 子窗户的个数13。 ■父亲见数学家仍然犹豫,又补充说: 口老大很小的时候家中没有其他孩子跟他一起玩。 ■你能说出3个孩子的年龄吗?
搜索“解空间” – 一个例子 一位父亲请一位数学家猜他3个孩子的年龄,他提示说: 3人年龄的乘积是36。 这时他们恰好经过一幢房子,父亲又提示说:他们年龄之和等于这房 子窗户的个数13。 父亲见数学家仍然犹豫,又补充说: 老大很小的时候家中没有其他孩子跟他一起玩。 你能说出3个孩子的年龄吗?
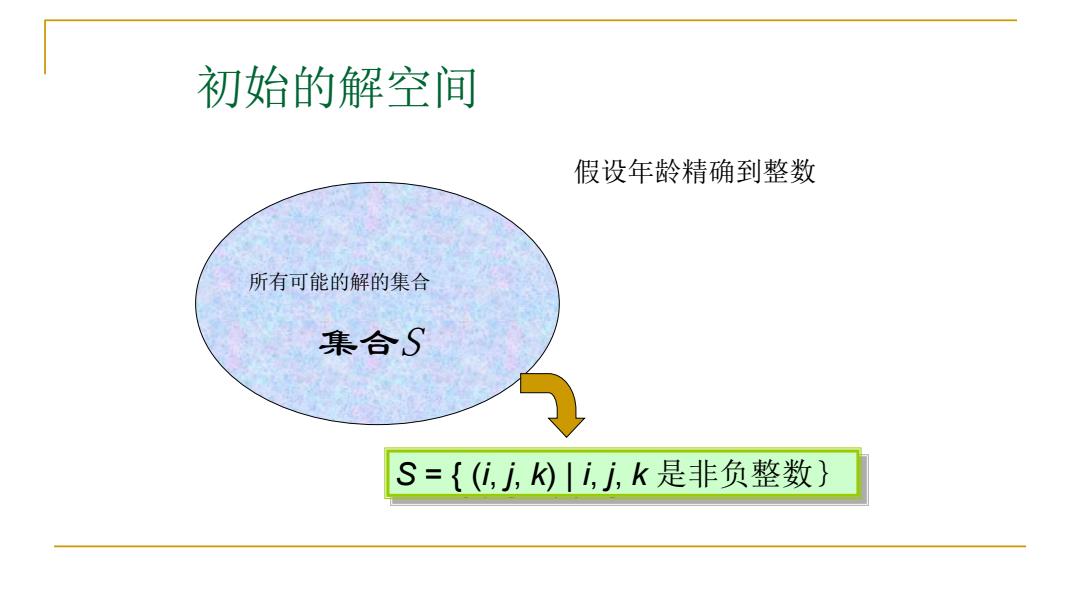
初始的解空间 假设年龄精确到整数 所有可能的解的集合 集合S S={(0,j,k)川i,j,k是非负整数}
初始的解空间 假设年龄精确到整数 集合S 所有可能的解的集合 S = { (i, j, k) | i, j, k 是非负整数}

利用条件缩小可能的解空间 S (1,1,36) (1,2,18) 所有可能的解的集合 (1,312) 集合S (1,4,9) (1,6,6) (2,2,9) (2,3,6) (3,3,4) 条件1:3人年龄乘积为36
利用条件缩小可能的解空间 集合S1 所有可能的解的集合 S1 : (1, 1, 36) (1, 2, 18) (1, 3, 12) (1, 4, 9) (1, 6, 6) (2, 2, 9) (2, 3, 6) (3, 3, 4) 条件1:3人年龄乘积为36
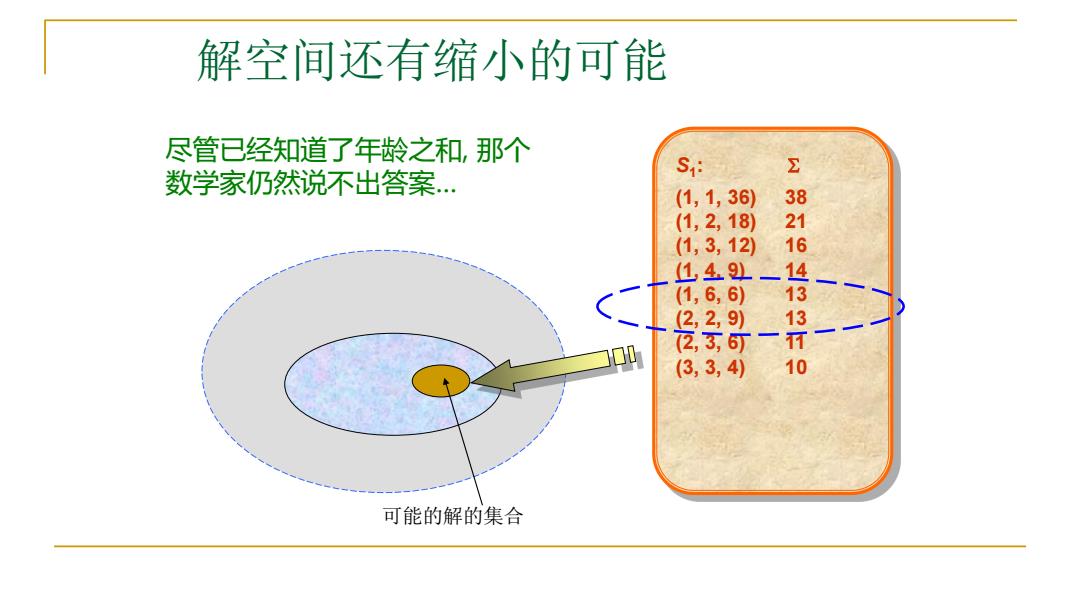
解空间还有缩小的可能 尽管已经知道了年龄之和,那个 数学家仍然说不出答案 S (1,1,36) (1,2,18) (1,3,12) 38116 1491 (1,6,6) 00 留 (3,3,4) 13T10 可能的解的集合
解空间还有缩小的可能 尽管已经知道了年龄之和, 那个 数学家仍然说不出答案… S1 : (1, 1, 36) 38 (1, 2, 18) 21 (1, 3, 12) 16 (1, 4, 9) 14 (1, 6, 6) 13 (2, 2, 9) 13 (2, 3, 6) 11 (3, 3, 4) 10 可能的解的集合

再进一步就是解! ■当前可能的解的集合: {(1,6,6),(2,2,9)} ·但是:老大没有同年龄的兄弟姐妹 ·因此三个孩子的年龄分别是: 9岁、2岁和2岁
再进一步就是解! 当前可能的解的集合: { (1,6,6), (2,2,9) } 但是:老大没有同年龄的兄弟姐妹. 因此三个孩子的年龄分别是: 9岁、2岁和2岁

问题求解的基本“方法” ·确定合理的解空间,并表示为某种“结构”。 ■利用已知的限制条件(知识)尽可能快的压缩可能的解空间。 口当解空间已经足够小,我们就可以“直接”解题。 如果很难确定解空间的范围,或者很难有效地缩小解空间,这 个题目就“很难
问题求解的基本“方法” 确定合理的解空间,并表示为某种“结构”。 利用已知的限制条件(知识)尽可能快的压缩可能的解空间。 当解空间已经足够小,我们就可以“直接”解题。 如果很难确定解空间的范围,或者很难有效地缩小解空间,这 个题目就“很难

搜索结构 end 128 广度优先-BFS 76 402 128 106 354 1018 02 112 39% 深度优先-DFS
搜索结构 深度优先 - DFS 广度优先 - BFS
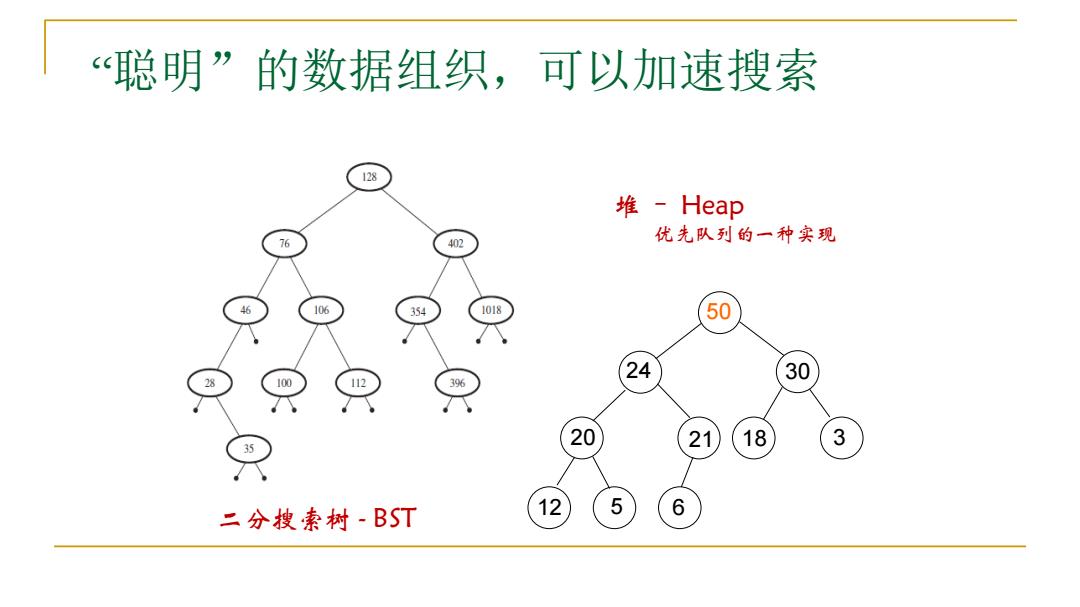
聪明”的数据组织,可以加速搜索 128 堆-Heap 402 优先队列的一种实现 76 106 354 1018 50 24 30 28 10 20 21 18 3 二分搜索树-BST 12 5 6
“聪明”的数据组织,可以加速搜索 二分搜索树 - BST 24 20 6 50 12 5 21 18 3 30 堆 – Heap 优先队列的一种实现