
计算思维引导 陶先平 南京大学计算机软件研究所
计算思维引导 陶先平 南京大学计算机软件研究所

找假币--何谓“计算思维”? 给你70个外观完全一样的金币,但是你知道 其中有一个是假币,其重量比真币轻。给你 一架没有砝码的天平,你可以在天平两边 摆任意多个金币,比较他们的轻重。 •请设计一种方法,通过若干次称量,确定 哪一个是假币
找假币---何谓“计算思维”? •给你70个外观完全一样的金币,但是你知道 其中有一个是假币,其重量比真币轻。给你 一架没有砝码的天平,你可以在天平两边 摆任意多个金币,比较他们的轻重。 •请设计一种方法,通过若干次称量,确定 哪一个是假币

第一个解法 总共称7次 w 雨平分称量。 ·将轻的一侧钙个加性意一个再平分称量。 ·将轻的一侧的3个加另外任意一个再平分称量。 ·将轻的一侧的2个分别放到天平两边,轻的是假币。完成
第一个解法 • 先将70个金币平均分两份,放到天平两边。 假币必在轻的那一侧的35个中。 • 将那35个加上另一侧中任意一个,再平分称量。 • 将轻的一侧的18个平分再称量。 • 将轻的一侧的9个加另外任意一个再平分称量。 • 将轻的一侧的5个加另外任意一个再平分称量。 • 将轻的一侧的3个加另外任意一个再平分称量。 • 将轻的一侧的2个分别放到天平两边,轻的是假币。完成 总共称7次

第一个解法稍稍改进 总共称6次 ·先将70个金币平均分两份,放到天平两边。 ·将那35个中红意个放穷,其金歌色益。 每边17个。 广年家的个中任个皮咨 香的二侧的8个平分再称量,每 边4个 但花 还能5 ·将轻的一侧的4个再平分标量,每边2个。 ·将轻的一侧的2个再平分称量,每边个。轻的是假币。完成
第一个解法稍稍改进 • 先将70个金币平均分两份,放到天平两边。 假币必在轻的那一侧的35个中。 • 将那35个中任意一个放一旁,其余再平分称量,每边17个。 • 若相等则旁边的是假币,否则将轻的一侧的17个中任意一个放旁 边,其余的再平分再称量,每边8个。 • 若相等则旁边的是假币,否则将轻的一侧的8个平分再称量,每 边4个 • 将轻的一侧的4个再平分称量,每边2个。 • 将轻的一侧的2个再平分称量,每边个。轻的是假币。完成 总共称6次
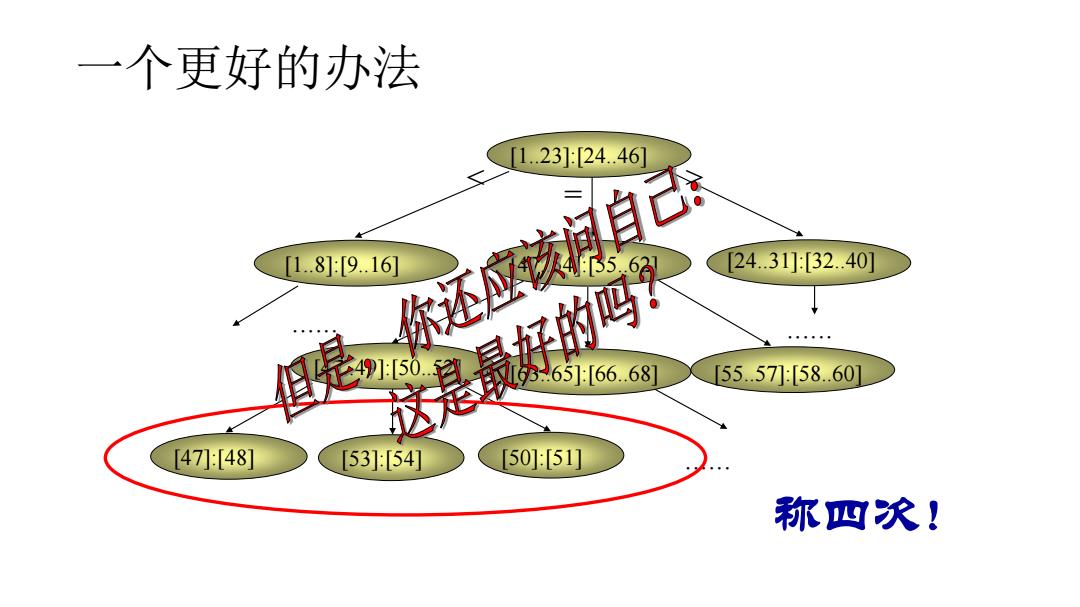
一个更好的办法 [1.23[24.46] 但遮东还的具、 [1.819.16] [24.31[32.40] [55.57[58.601 [47:[48] 1531:[54] 50]:[51] 称四次!
一个更好的办法 [1..23]:[24..46] [1..8]:[9..16] [47..54]:[55..62] [24..31]:[32..40] ...... ...... [47..49]:[50..52] [63..65]:[66..68] [55..57]:[58..60] [47]:[48] [53]:[54] [50]:[51] ...... 称四次!

我们为什么会这样思考来找到最快的方法? 问题空间: 我们所观察到的对象 (每个对象的状态及其变化) 第一种方案: 第二种方案: 几乎每次压缩问题空间到一半 几乎每次压缩问题空间到三分之一
我们为什么会这样思考来找到最快的方法? 第一种方案: 问题空间: 我们所观察到的对象 (每个对象的状态及其变化) 第二种方案: 几乎每次压缩问题空间到一半 几乎每次压缩问题空间到三分之一√

如何表达我们的这个思想?写个程序! Procedure Findlt(n){ ∥从n个硬币中找出一个较轻的假币 if n=2{ ∥只有两个硬币 天平上翘起的是假币;程序结束; } if n=3{ ∥有三个硬币 任取两个放在天平上: 如果平衡,假币为第三个,否则为翘起的天平端硬币;程序结束; else{ 川有多于三个硬币 将硬币分为几乎数量相同的三堆n1,n2,n3; /其中必定有两堆数量相同 称量其中数量相同的两堆; /不妨假设n1=n2 如果两堆不同重{ /不妨假设n1堆轻 Findlt(n1); else Findlt(n3); }
如何表达我们的这个思想?写个程序! Procedure FindIt(n) { //从n个硬币中找出一个较轻的假币 if n=2 { //只有两个硬币 天平上翘起的是假币;程序结束; } if n=3 { //有三个硬币 任取两个放在天平上; 如果平衡,假币为第三个,否则为翘起的天平端硬币;程序结束; } else { //有多于三个硬币 将硬币分为几乎数量相同的三堆n1,n2,n3; //其中必定有两堆数量相同 称量其中数量相同的两堆; //不妨假设n1=n2 如果两堆不同重 { //不妨假设n1堆轻 FindIt(n1); } else FindIt(n3); } }

到此为止,这个问题我们解决了吗? No! 我们还应该至少回答这些问题: 你能证明你的解法是正确的吗? 你能证明你的解法是最优的吗? 你能证明你的程序没有错误吗? 9/24/2015
到此为止,这个问题我们解决了吗? No! 我们还应该至少回答这些问题: 你能证明你的解法是正确的吗? 你能证明你的解法是最优的吗? 你能证明你的程序没有错误吗? 9/24/2015

再一个互动游戏: 统计到场人数: 0,所有人都站起来,每个人都握有一个 数字:1 1,每两个人组成一组,将手中数字相加, 并记住。其中一人坐下; •2,重复第一步,直到教室中只有一人; 3,最后一人,大声报出数字;
再一个互动游戏: •统计到场人数: •0,所有人都站起来,每个人都握有一个 数字:1 •1,每两个人组成一组,将手中数字相加, 并记住。其中一人坐下; •2,重复第一步,直到教室中只有一人; •3,最后一人,大声报出数字;

这个游戏,给了我们什么启发?
这个游戏,给了我们什么启发?