
计算机问题求解一论题3-8 单源最短通路算法 2016年10月26日
计算机问题求解 – 论题3-8 - 单源最短通路算法 2016年10月26日

什么是最短通路问题? In a shortest-paths problem,we are given a weighted,directed graph G=(V,E),with weight function w:ER mapping edges to real-valued weights.The weight w(p)of path p=(vo,v1,...,v)is the sum of the weights of its constituent edges: 问题: k w(p)=∑w(-4,). 偷入是什么?喻 i=1 :是什么? We define the shortest-path weight &(u,v)from u to v by 8u,)= minw(p):uv if there is a path from u tov, 00 otherwise A shortest path from vertex u to vertex v is then defined as any path p with weight w(p)=6u,v)
什么是最短通路问题?

问题2: 为什么说可以将单源最短路问 题的解看成一个树?你认为这 个树与两种图遍历搜索树相比, 更可能象哪一个?

As in breadth-first search,we shall be interested in the predecessor subgraph G=(Vz,Ex)induced by the n values.Here again,we define the vertex set V to be the set of vertices of G with non-NIL predecessors, plus the source s: Vx={v∈V:u.π≠NIL}U{s}. The directed edge set E is the set of edges induced by the values for vertices in V: Em={(v.π,v)∈E:v∈Vx-{s}. A shortest-paths tree rooted at s is a directed subgraph G'=(V',E). where v'V and E'C E,such that 1.V'is the set of vertices reachable froms in G, 2.G'forms a rooted tree with root s,and 3.for all vV,the unique simple path from s to v in G'is a shortest path froms to v in G. Predecessor-subgraph property (Lemma 24.17) Once v.d=8(s.v)for all vV.the predecessor subgraph is a shortest-paths tree rooted at s
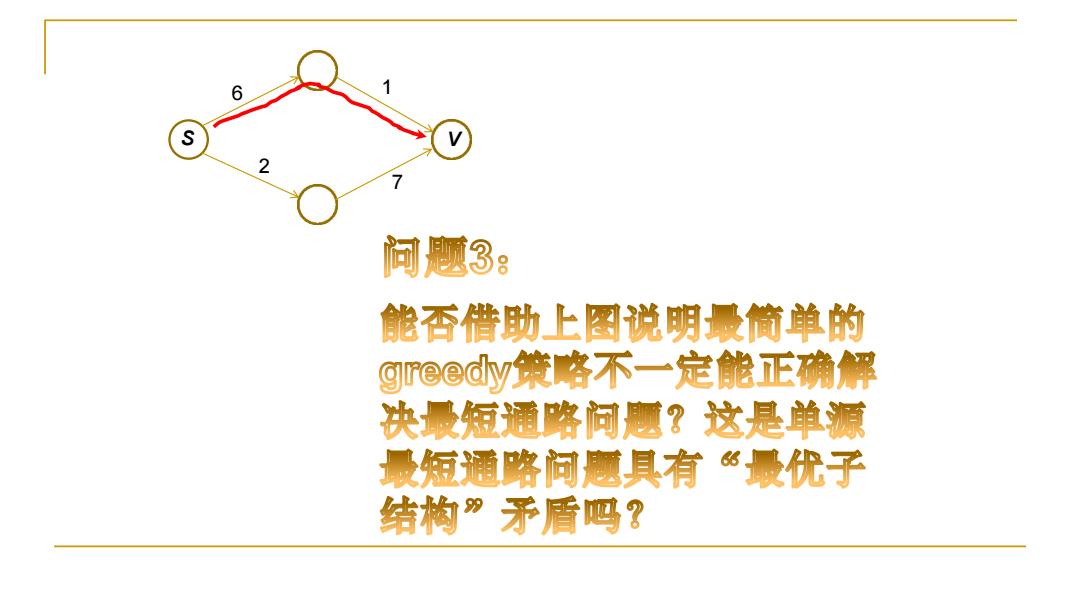
6 问题3: 能否借助上图说明最简单的 greed小y策咯不一定能正确解 决最短通路问题?这是单源 最短通路问意具有“最优子 结构”矛盾吗?
s 2 6 1 7 v

问题4: 具有负值权的回路对于单源 最短通路问题的解有什么影 响?非负值权的回路呢?

问题5: 在本章中介绍的算法基本 思路是一样的,那是什么?
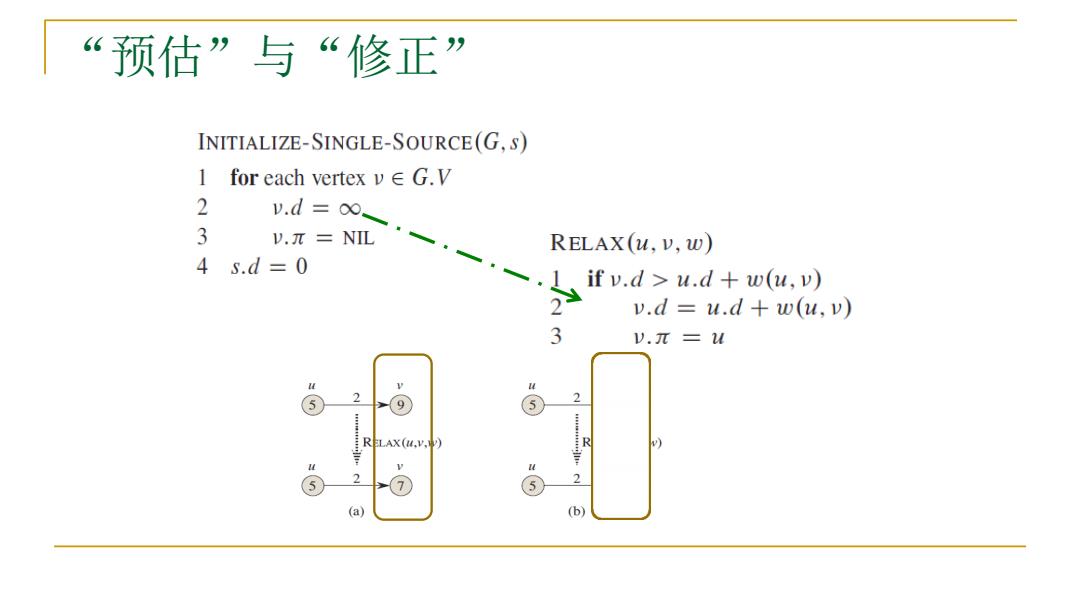
6“ 预估”与“修正” INITIALIZE-SINGLE-SOURCE(G,S) 1 for each vertex v∈G.V 2 v.d=00、 3 v.π=NL· RELAX(u,v,w) 4s.d=0 I if v.d>u.d+w(u,v) v.d u.d+w(u,v) 3 V.元=u 2 >⑨ ⑤ RELAX(u.V.W) 9⑦ ⑤ 2 (a) (b)
“预估”与“修正
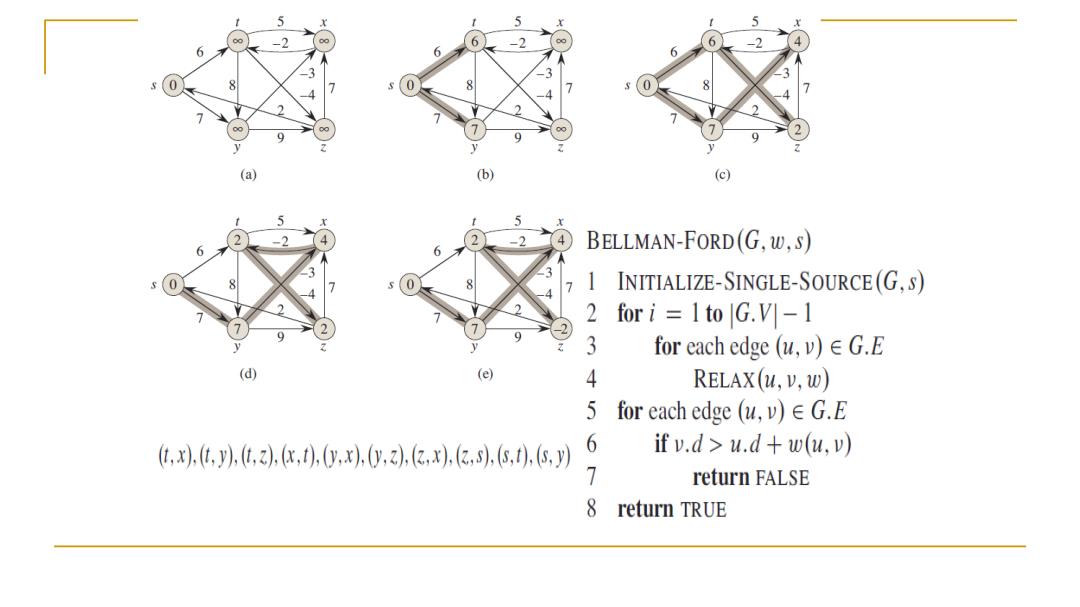
6 (a) (b) (c) 6 BELLMAN-FORD(G,w,s) 0 1 INITIALIZE-SINGLE-SOURCE(G.s) 2 for i 1to G.V]-1 3 for each edge (u,v)G.E (d) (e) 4 RELAX(u,v,w) 5 for each edge (u,v)G.E ,,,,,,),0,x,,2亿,x,,,,,,以 6 if v.d>u.d+w(u,v) 7 return FALSE 8 return TRUE

问题6: Relax中的“修正”到底在 干什么?