
计算机问题求解一论题1-11 有限与无限 2015年12月10日
计算机问题求解 – 论题1-11 - 有限与无限 2015年12月10日

“聪明的经理”、“非常聪明的经理” 和“非常非常聪明的经理” 问题1: 你能给我 田 们讲讲这 个故事吗? 满
“聪明的经理”、“非常聪明的经理” 和“非常非常聪明的经理

集合的等势 To make precise what it means for two sets (even two infinite sets)to have the same number of elements,we need a definition. We say that a set A is equivalent to a set B if there exists a bijection f:AB.We write AB for A is equivalent to B.(Other authors use the words equipotent or equinumerous. 问题2 你原来脑海中的两个集合元素一样多” 的概念是什么样的呢?对无穷集合适用吗?
集合的等势

问题3:如何精确定义什么是有限集? We say that a set S is finite ifeither =0or if is equivalent to the set(123... forsme positive integer 更加数学化的表述:(每一个自然数也是一个集合) 空集记为0; 如果是自然数,则其"后继”为:k心3。 于是: 有限集就是与某个自然数等势的集合
问题3:如何精确定义什么是有限集? 更加数学化的表述:(每一个自然数也是一个集合) 空集记为0; 如果k是自然数,则其“后继”为: k {k} 。 于是: 有限集就是与某个自然数等势的集合

问题4: 什么是无限集合? 提示:有限集就是与某个自然数等势的集合
提示:有限集就是与某个自然数等势的集合
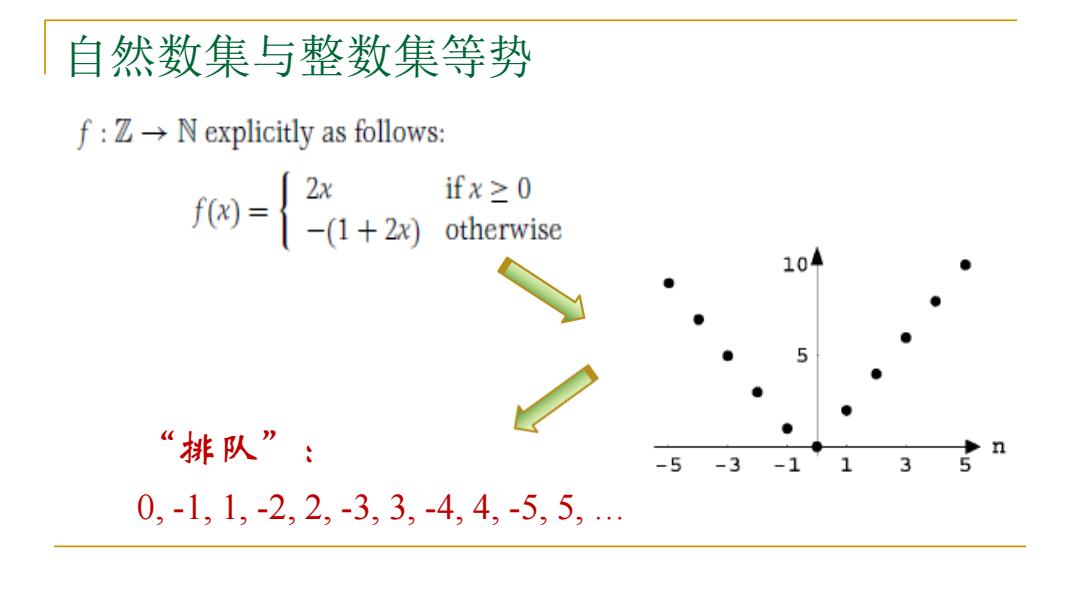
自然数集与整数集等势 f:ZN explicitly as follows: f-{+2刘 2x ifx≥0 otherwise 104 5 “排队”: -5-3 -1 0,-1,1,-2,2,-3,3,-4,4,-5,5
自然数集与整数集等势 “排队”: 0, -1, 1, -2, 2, -3, 3, -4, 4, -5, 5, …

问题5: 63,-2,-1,0,1,2,39不 能算排好队”了,为什么?

关于双射的证明(1) f:ZN explicitly as follows: 注意: 2x f=1 ifx≥0 不能遗漏了case3! -(1+2x)otherwise Proof that f is one-to-one. Letm,n∈Z and suppose that f(m)≠f(n). Case 1.Suppose that m 0 and n z0.Then f(m)=2m and f(n)=2n.Thus 2m =2n,and therefore m =n. Case 2.Suppose that m<0 and n 0.Then f(m)=-2m-1 and f(n)=-2n-1.Thus,-2m-1 =-2n-1,and therefore m n. Case 3.Suppose that one of the two,say m,is nonnegative,and the other is negative.Then f(m)=2m and f(n)=-2n-1. Thus 2m =-2n-1.But this means that an even number, 2m,is equal to an odd number,-2n-1,which is impossible. Therefore,if f(m)=f(n),only case 1 and case 2 can occur.In either of these cases,we have shown that m n.Thus f is one-to- one. ■
关于双射的证明 (1) 注意: 不能遗漏了case 3!

关于双射的证明(2) f ZN explicitly as follows: ifx≥0 -1+2) otherwise Proof that f maps Z onto N. Letk∈N.If k is even,then k=2 m for some m∈Z with m≥0. Thus,m e Z and f(m)=2m k.If k is odd,then k+1 is even. Hence m =(k+1)/(-2)EZ.Since k z 1,we have m 0.Thus, f(m)=-2m-1 =-2((k+1)/(-2))-1 k.We conclude that for allk∈N,there exists m∈Z such that f(m)=k.Since f:Z→Nis a well-defined function,f maps Z onto N. ■
关于双射的证明 (2)

无穷不仅仅是“很多很多” 伽利略悖论: 整体与局部“一样大”】
无穷不仅仅是“很多很多” 伽利略悖论: 整体与局部“一样大”!