
计算机问题求解一论题2-5 分治法与递归 2016年03月24日
计算机问题求解 – 论题2-5 - 分治法与递归 2016年03月24日

Mergesort Revisited MERGE-SORT (A,p.r) 1 if p<r 2 q=L(p+r)/2」 3 MERGE-SORT(A,p,q) 4 MERGE-SORT(A,q 1,r) 5 MERGE(A,p,q,r) 问题1: 这个算法究竟是如何“排”序的?
Mergesort Revisited
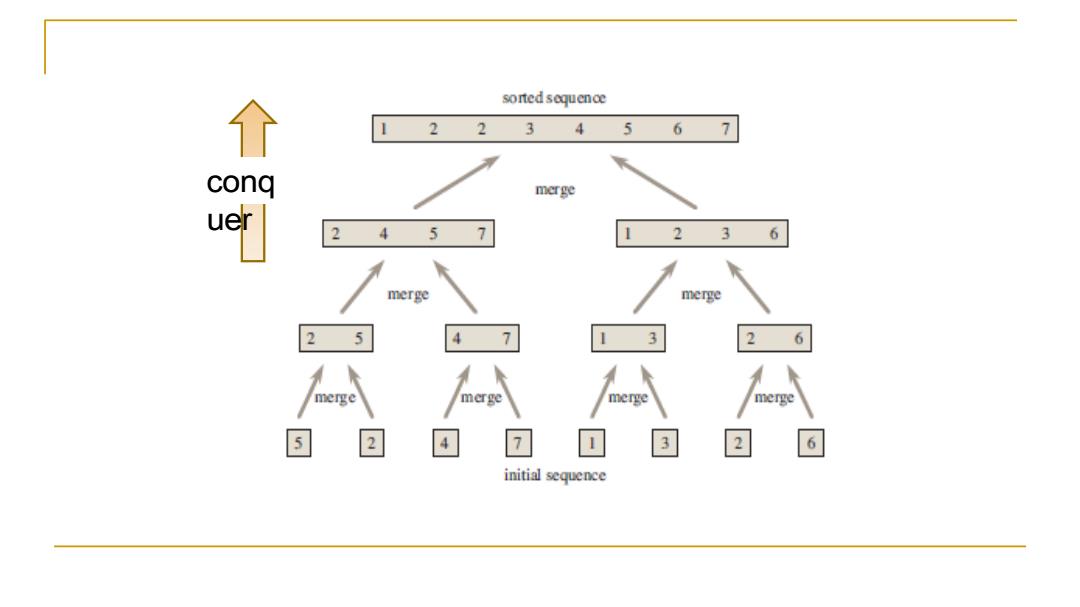
sorted sequence 个 1 2 3 5 6 7 conq merge 2 4 5 7 1 2 3 6 merge merge 2 5 4 3 6 merge merge merge merge 回 回 回 3 6 initial sequence
5 2 4 7 1 3 2 6 5 2 4 7 1 3 2 6 Divid e Divide further, until… conq uer

问题2: 人的思维分而治之” 如何变为算法策咯的呢?

间题3: 如何考虑分治算法的代价? 递归代价与非递归代价
递归代价与非递归代价

导出递归式 MERGE-SORT (A,p,r) 1 if p1
导出递归式 两次递归,理想情 况下每次问题规模 是原来的一半。 非递归开销
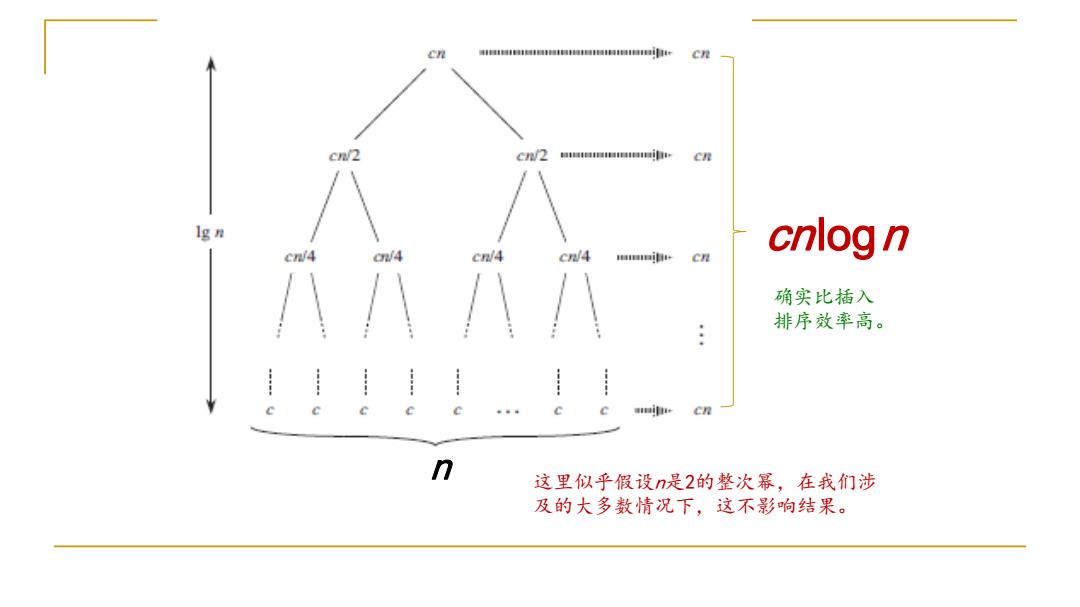
cn C星 cn/2 cn2 C月 1gn c/4 cnlog n /4 cn/4 cn/4 C 确实比插入 排序效率高。 国自+ cn n 这里似乎假设n是2的整次幂,在我们涉 及的大多数情况下,这不影响结果
n cnlogn 确实比插入 排序效率高。 这里似乎假设n是2的整次幂,在我们涉 及的大多数情况下,这不影响结果

问题4: 书上的投资回报问题是怎样 被转化为最大子数组问题的?
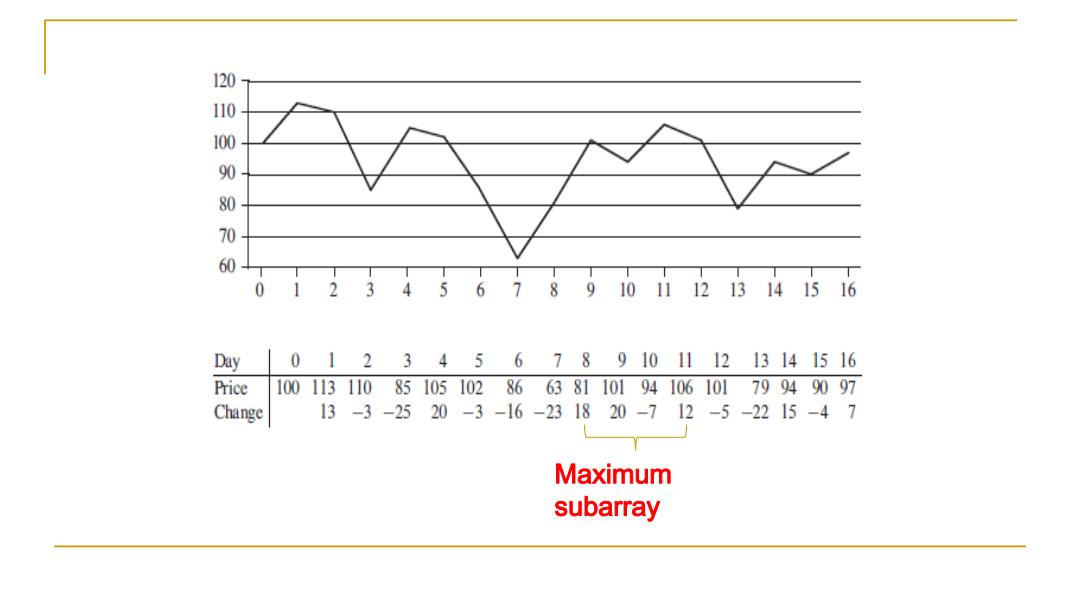
50000006 0 2345678910111213141516 Day 012345678910111213141516 Price 100113110851051028663811019410610179949097 Change 13-3-2520-3-16-231820-712-5-2215-47 Maximum subarray
Maximum subarray
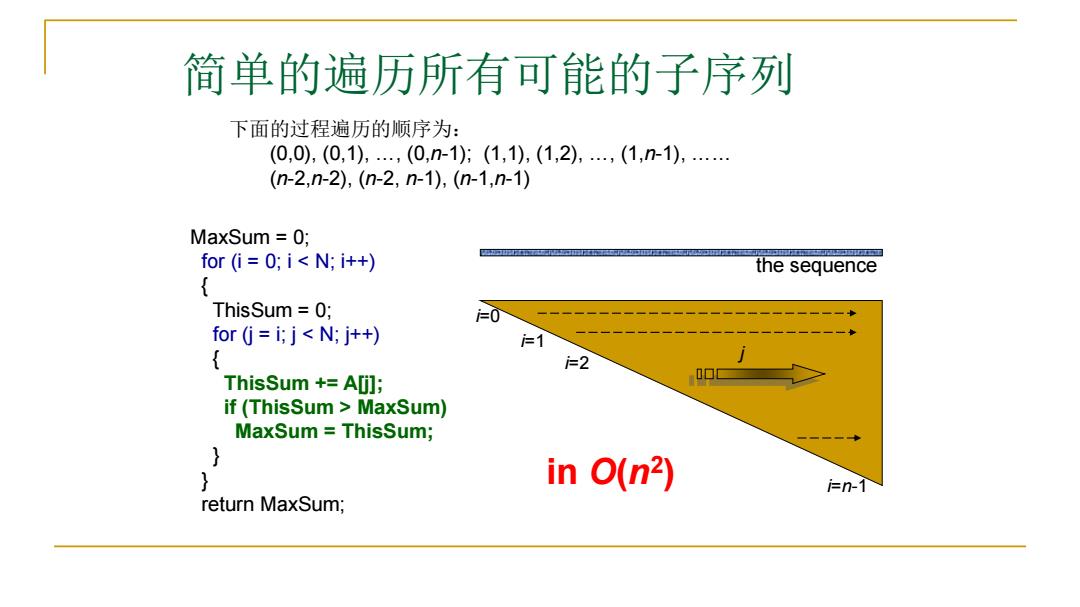
简单的遍历所有可能的子序列 下面的过程遍历的顺序为: (0,0),(0,1),,(0,n-1);(1,1),(1,2),,(1,n-1),.… (n-2,n-2),(n-2,n-1),(n-1,n-1) MaxSum 0; for (i=0;i<N;i++) the sequence ThisSum =0; =0 一一一一◆ for (j=i;j<N;j++) 1 =2 ThisSum +A[j]; if(ThisSum MaxSum) MaxSum ThisSum; 一一一 } in O(n2) i=n-1 return MaxSum;
简单的遍历所有可能的子序列 MaxSum = 0; for (i = 0; i MaxSum) MaxSum = ThisSum; } } return MaxSum; the sequence i=0 i=1 i=2 i=n-1 j in O(n2 ) 下面的过程遍历的顺序为: (0,0), (0,1), …, (0,n-1); (1,1), (1,2), …, (1,n-1), …… (n-2,n-2), (n-2, n-1), (n-1,n-1)