
计算机问题求解一论题3-11 -图旅行 2016年11月16日
计算机问题求解 – 论题3-11 - 图旅行 2016年11月16日
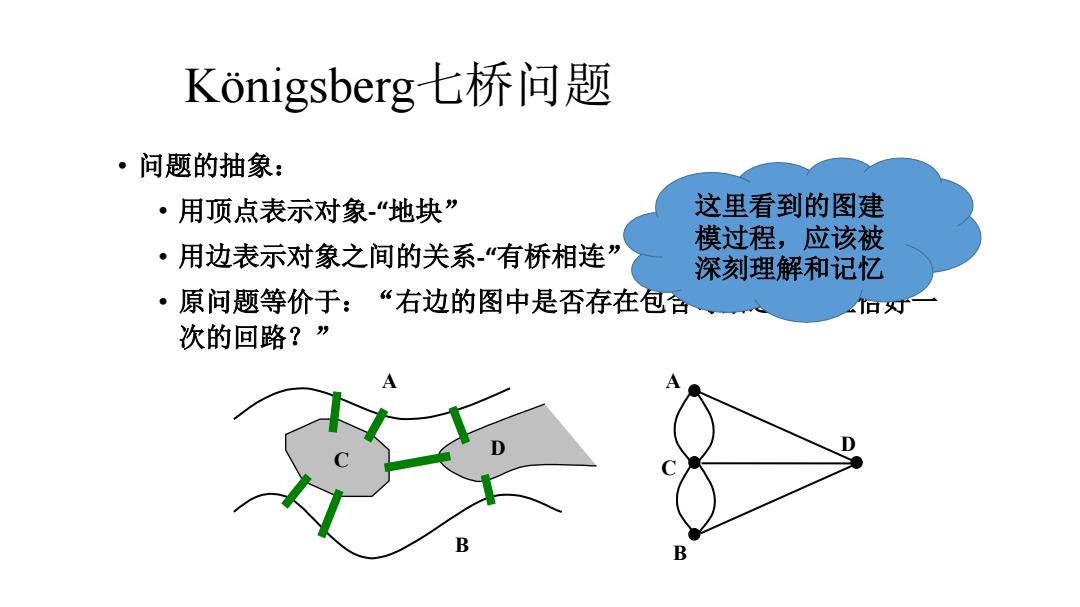
Konigsberg七桥问题 ·问题的抽象: ·用顶点表示对象“地块” 这里看到的图建 模过程,应该被 ·用边表示对象之间的关系“有桥相连” 深刻理解和记忆 ·原问题等价于:“右边的图中是否存在包合 何灯一 次的回路?” B
Königsberg七桥问题 • 问题的抽象: • 用顶点表示对象-“地块” • 用边表示对象之间的关系-“有桥相连” • 原问题等价于:“右边的图中是否存在包含每条边一次且恰好一 次的回路?” C D A B A C B D 这里看到的图建 模过程,应该被 深刻理解和记忆
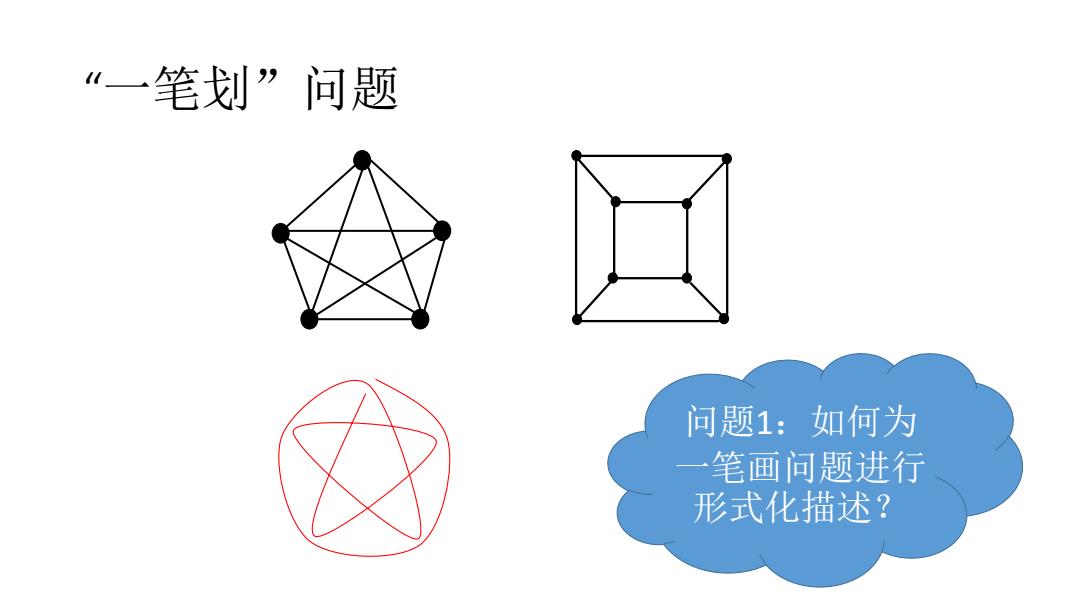
一笔划”问题 问题1:如何为 一 笔画问题进行 形式化描述?
“一笔划”问题 问题1:如何为 一笔画问题进行 形式化描述?

欧拉通路和欧拉▣路 ·定义:包含图(无向图或有向图)中每条边的简单通路称为欧拉通 路。 注意:欧拉通路是简单通路(边不重复),但顶点可重复 ·定义:包含图中每条边的简单回斗 如果图G中含欧拉回路, o 问题2:你能够想象 但没有欧拉回路,则G 欧拉是如何思考这 /备注:通常假设G是连 个问题的吗?
欧拉通路和欧拉回路 • 定义:包含图(无向图或有向图)中每条边的简单通路称为欧拉通 路。 注意:欧拉通路是简单通路(边不重复),但顶点可重复 • 定义:包含图中每条边的简单回路称为欧拉回路。 • 如果图G中含欧拉回路,则G称为欧拉图。如果图G中有欧拉通路, 但没有欧拉回路,则G称为半欧拉图。 //备注:通常假设G是连通的。 问题2:你能够想象 欧拉是如何思考这 个问题的吗?

欧拉图中的顶点度数 ·连通图G是欧拉图当且仅当G中每个顶点的度数均为偶数。 ·证明: →设C是G中的欧拉回路,则VveVG d(y)必等于v在C上出现数的2倍(起 点与终点看成出现一次)。 可以证明: (1)G中所有的边可以分为若干边不相交的简单回路。 (2)这些回路可以串成一个欧拉回路
欧拉图中的顶点度数 • 连通图G是欧拉图 当且仅当 G中每个顶点的度数均为偶数。 • 证明: 设C是G中的欧拉回路,则vVG , d(v)必等于v在C上出现数的2倍(起 点与终点看成出现一次)。 可以证明: (1)G中所有的边可以分为若干边不相交的简单回路。 (2)这些回路可以串成一个欧拉回路

全偶度图中的回路 ·若图G中任一顶点均为偶度点,则G中所有的边包含在若干边不相交的简 单回路中。 ·证明:对G的边数m施归纳法。 ·当m=1,G是环,结论成立。假设m≤k(k21)时结论成立。 ·考虑m=k+1的情况:注意δ≥2,G中必含简单回路,记为C,令 G=G-E。,设G中含s个连通分支,显然,每个连通分支内各点均为 偶数(包括0),且边数不大于k。则根据归纳假设,每个非平凡的连 通分支中所有边含于没有公共边的简单回路中,注意各连通分支以 及C两两均无公共边,于是,结论成立
全偶度图中的回路 • 若图G中任一顶点均为偶度点,则G中所有的边包含在若干边不相交的简 单回路中。 • 证明:对G的边数m施归纳法。 • 当m=1, G是环,结论成立。假设mk(k1)时结论成立。 • 考虑m=k+1的情况:注意G2, G中必含简单回路,记为C,令 G‘=G-EC , 设G’中含s个连通分支,显然,每个连通分支内各点均为 偶数(包括0),且边数不大于k。则根据归纳假设,每个非平凡的连 通分支中所有边含于没有公共边的简单回路中,注意各连通分支以 及C两两均无公共边,于是,结论成立

若干小回路串成欧拉回路 ·若连通图G中所有的边包含在若干边不相交的简单回路中,则G中含欧拉 回路。 ·证明:对G中简单回路个数施归纳法。当=1时显然。 ·假设dkk21)时结论成立。考虑d=k+1. ·按某种方式对k+1个简单回路排序,令G=G-E(Ck+),设G中含s个连 通分支,则每个非平凡分支所有的边包含在相互一 路中,且回路个数不大于k。由归纳假 问题3:你能够从 欧拉图,设其欧拉回路是C。因G连 G中的欧拉回路构造如下:从Ck+ 这样的数学归纳法 边,每当遇到一个尚未遍历的C'与 中,看到寻找欧拉 上的边,回到v'继续沿Ck进行。 回路的算法吗?
若干小回路串成欧拉回路 • 若连通图G中所有的边包含在若干边不相交的简单回路中,则G中含欧拉 回路。 • 证明:对G中简单回路个数d施归纳法。当d=1时显然。 • 假设dk(k1)时结论成立。考虑d=k+1. • 按某种方式对k+1个简单回路排序,令G‘=G-E(Ck+1),设G’中含s个连 通分支,则每个非平凡分支所有的边包含在相互没有公共边的简单回 路中,且回路个数不大于k。由归纳假设,每个非平凡连通分支Gi均为 欧拉图,设其欧拉回路是Ci '。因G连通,故Ck+1与诸Ci ’都有公共点。 • G中的欧拉回路构造如下:从Ck+1上任一点(设为v0 )出发遍历Ck+1上的 边,每当遇到一个尚未遍历的Ci '与Ck+1的交点(设为vi '), 则转而遍历Ci ' 上的边,回到vi '继续沿Ck+1进行。 问题3:你能够从 这样的数学归纳法 中,看到寻找欧拉 回路的算法吗?

关于欧拉图的等价命题 ·设G是非平凡连通图,以下三个命题等价: (1)G是欧拉图。 (2)G中每个顶点的度数均为偶数。 (3)G中所有的边包含在相互没有公共边的简单回路中
关于欧拉图的等价命题 • 设G是非平凡连通图,以下三个命题等价: (1) G是欧拉图。 (2) G中每个顶点的度数均为偶数。 (3) G中所有的边包含在相互没有公共边的简单回路中

半欧拉图的判定 ·设G是连通图,G是半欧拉图当且仅当G恰有两个奇度点。 ·证明: →设P是G中的欧拉通路(非回路),设P的始点与终点分别是u,y,则对G 中任何一点x,若x非u,V,则x的度数等于在P中出现次数的2倍,而u,y 的度数则是它们分别在P中间位置出现的次数的两倍再加1。 ←设G中两个奇度顶点是u,y,则G+v是欧拉图,设欧拉回路是C,则C 中含uv边,.C-uv是G中的欧拉通路。(这表明:如果试图一笔画出 一个半欧拉图,必须以两个奇度顶点为始点和终点。)
半欧拉图的判定 • 设G是连通图,G是半欧拉图 当且仅当 G恰有两个奇度点。 • 证明: 设P是G中的欧拉通路(非回路),设P的始点与终点分别是u,v, 则对G 中任何一点x, 若x非u,v,则x的度数等于在P中出现次数的2倍,而u,v 的度数则是它们分别在P中间位置出现的次数的两倍再加1。 设G中两个奇度顶点是u,v, 则G+uv是欧拉图,设欧拉回路是C, 则C 中含uv边,C-uv是G中的欧拉通路。(这表明:如果试图一笔画出 一个半欧拉图,必须以两个奇度顶点为始点和终点。)
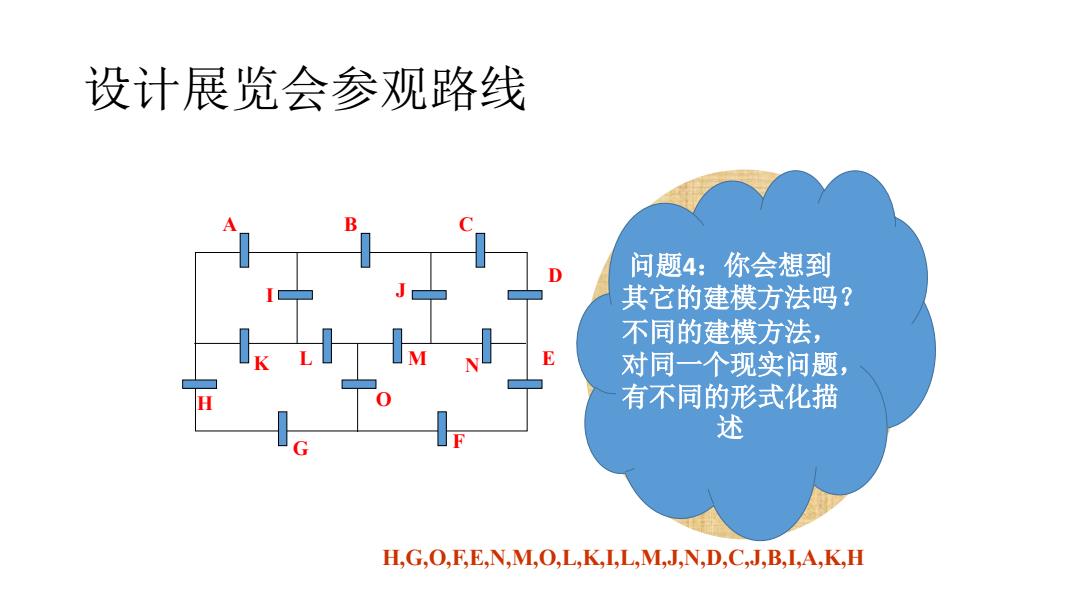
设计展览会参观路线 问题4:你会想到 其它的建模方法吗? 不同的建模方法, 对同一个现实问题, 有不同的形式化描 述 H,G,O,F,E,N,M,O,L,K,IL,M,J,N,D,C,J,B,I,A,K,H
设计展览会参观路线 A B C J E F I K H G D L M N O A B C I J D K L M N H O E G F H,G,O,F,E,N,M,O,L,K,I,L,M,J,N,D,C,J,B,I,A,K,H 问题4:你会想到 其它的建模方法吗? 不同的建模方法, 对同一个现实问题, 有不同的形式化描 述