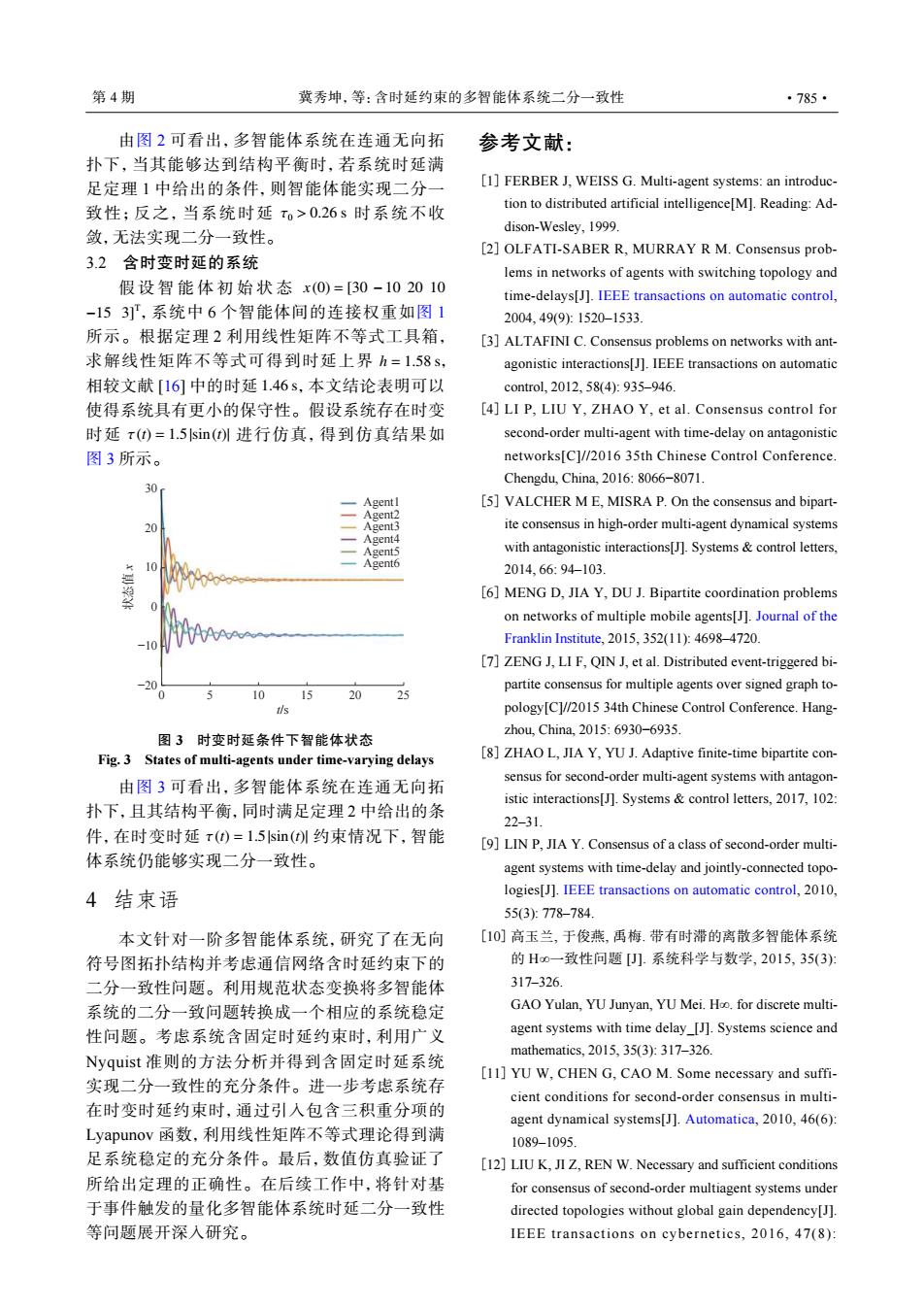
第4期 冀秀坤，等：含时延约束的多智能体系统二分一致性 ·785· 由图2可看出，多智能体系统在连通无向拓 参考文献： 扑下，当其能够达到结构平衡时，若系统时延满 足定理1中给出的条件，则智能体能实现二分一 [1]FERBER J.WEISS G.Multi-agent systems:an introduc- 致性；反之，当系统时延T。>026s时系统不收 tion to distributed artificial intelligence[M].Reading:Ad- dison-Wesley,1999 敛，无法实现二分一致性。 [2]OLFATI-SABER R,MURRAY R M.Consensus prob- 3.2含时变时延的系统 lems in networks of agents with switching topology and 假设智能体初始状态x(0)=[30-102010 time-delays[J].IEEE transactions on automatic control. -153],系统中6个智能体间的连接权重如图1 2004,49(9):1520-1533 所示。根据定理2利用线性矩阵不等式工具箱， [3]ALTAFINI C.Consensus problems on networks with ant- 求解线性矩阵不等式可得到时延上界h=1.58s, agonistic interactions[].IEEE transactions on automatic 相较文献[16]中的时延1.46s,本文结论表明可以 control,2012.58(4):935-946. 使得系统具有更小的保守性。假设系统存在时变 [4]LI P,LIU Y,ZHAO Y,et al.Consensus control for 时延t(d)=1.5sin()l进行仿真，得到仿真结果如 second-order multi-agent with time-delay on antagonistic 图3所示。 networks[C]//2016 35th Chinese Control Conference. Chengdu,China,2016:8066-8071. 30 -Agentl [5]VALCHER M E.MISRA P.On the consensus and bipart- Agent2 20 Agent3 ite consensus in high-order multi-agent dynamical systems Agent4 Agent5 with antagonistic interactions[J].Systems control letters. 10 Agent6 2014.66:94-103 [6]MENG D,JIA Y,DU J.Bipartite coordination problems 0 on networks of multiple mobile agents[J].Journal of the -10 Franklin Institute,2015,352(11):4698-4720 [7]ZENG J,LI F,QIN J,et al.Distributed event-triggered bi- -20 partite consensus for multiple agents over signed graph to- 10 15 20 25 tis pology[C]//2015 34th Chinese Control Conference.Hang- zhou,China,2015:6930-6935 图3时变时延条件下智能体状态 Fig.3 States of multi-agents under time-varying delays [8]ZHAO L,JIA Y,YU J.Adaptive finite-time bipartite con- 由图3可看出，多智能体系统在连通无向拓 sensus for second-order multi-agent systems with antagon- istic interactions[J].Systems control letters,2017,102: 扑下，且其结构平衡，同时满足定理2中给出的条 22-31. 件，在时变时延t()=1.5sin(训约束情况下，智能 [9]LIN P,JIA Y.Consensus of a class of second-order multi- 体系统仍能够实现二分一致性。 agent systems with time-delay and jointly-connected topo- 4结束语 logies[J].IEEE transactions on automatic control,2010, 55(3):778-784 本文针对一阶多智能体系统，研究了在无向 [10]高玉兰，于俊燕，禹梅.带有时滞的离散多智能体系统 符号图拓扑结构并考虑通信网络含时延约束下的 的Ho一致性问题J】.系统科学与数学，2015,35(3)： 二分一致性问题。利用规范状态变换将多智能体 317-326. 系统的二分一致问题转换成一个相应的系统稳定 GAO Yulan,YU Junyan,YU Mei.Hoo.for discrete multi- 性问题。考虑系统含固定时延约束时，利用广义 agent systems with time delay_[J].Systems science and mathematics,.2015,35(3:317-326 Nyquist准则的方法分析并得到含固定时延系统 [11]YU W.CHEN G,CAO M.Some necessary and suffi- 实现二分一致性的充分条件。进一步考虑系统存 cient conditions for second-order consensus in multi- 在时变时延约束时，通过引入包含三积重分项的 agent dynamical systems[J].Automatica,2010,46(6): Lyapunov函数，利用线性矩阵不等式理论得到满 1089-1095 足系统稳定的充分条件。最后，数值仿真验证了 [12]LIU K,JI Z,REN W.Necessary and sufficient conditions 所给出定理的正确性。在后续工作中，将针对基 for consensus of second-order multiagent systems under 于事件触发的量化多智能体系统时延二分一致性 directed topologies without global gain dependency[J]. 等问题展开深人研究。 IEEE transactions on cybernetics,2016,47(8)τ0 > 0.26 s 由图 2 可看出，多智能体系统在连通无向拓 扑下，当其能够达到结构平衡时，若系统时延满 足定理 1 中给出的条件，则智能体能实现二分一 致性；反之，当系统时延 时系统不收 敛，无法实现二分一致性。 3.2 含时变时延的系统 x (0) = [30 −10 20 10 −15 3]T h = 1.58 s 1.46 s τ(t) = 1.5|sin(t)| 假设智能体初始状态 ，系统中 6 个智能体间的连接权重如图 1 所示。根据定理 2 利用线性矩阵不等式工具箱， 求解线性矩阵不等式可得到时延上界 ， 相较文献 [16] 中的时延 ，本文结论表明可以 使得系统具有更小的保守性。假设系统存在时变 时延 进行仿真，得到仿真结果如 图 3 所示。 Agent1 Agent2 Agent3 Agent4 Agent5 Agent6 −20 −10 0 0 5 10 15 20 25 10 20 30 状态值 x t/s 图 3 时变时延条件下智能体状态 Fig. 3 States of multi-agents under time-varying delays τ(t) = 1.5|sin(t)| 由图 3 可看出，多智能体系统在连通无向拓 扑下，且其结构平衡，同时满足定理 2 中给出的条 件，在时变时延 约束情况下，智能 体系统仍能够实现二分一致性。 4 结束语 本文针对一阶多智能体系统，研究了在无向 符号图拓扑结构并考虑通信网络含时延约束下的 二分一致性问题。利用规范状态变换将多智能体 系统的二分一致问题转换成一个相应的系统稳定 性问题。考虑系统含固定时延约束时，利用广义 Nyquist 准则的方法分析并得到含固定时延系统 实现二分一致性的充分条件。进一步考虑系统存 在时变时延约束时，通过引入包含三积重分项的 Lyapunov 函数，利用线性矩阵不等式理论得到满 足系统稳定的充分条件。最后，数值仿真验证了 所给出定理的正确性。在后续工作中，将针对基 于事件触发的量化多智能体系统时延二分一致性 等问题展开深入研究。 参考文献： FERBER J, WEISS G. Multi-agent systems: an introduc￾tion to distributed artificial intelligence[M]. Reading: Ad￾dison-Wesley, 1999. [1] OLFATI-SABER R, MURRAY R M. Consensus prob￾lems in networks of agents with switching topology and time-delays[J]. IEEE transactions on automatic control, 2004, 49(9): 1520–1533. [2] ALTAFINI C. Consensus problems on networks with ant￾agonistic interactions[J]. IEEE transactions on automatic control, 2012, 58(4): 935–946. [3] LI P, LIU Y, ZHAO Y, et al. Consensus control for second-order multi-agent with time-delay on antagonistic networks[C]//2016 35th Chinese Control Conference. Chengdu, China, 2016: 8066−8071. [4] VALCHER M E, MISRA P. On the consensus and bipart￾ite consensus in high-order multi-agent dynamical systems with antagonistic interactions[J]. Systems & control letters, 2014, 66: 94–103. [5] MENG D, JIA Y, DU J. Bipartite coordination problems on networks of multiple mobile agents[J]. Journal of the Franklin Institute, 2015, 352(11): 4698–4720. [6] ZENG J, LI F, QIN J, et al. Distributed event-triggered bi￾partite consensus for multiple agents over signed graph to￾pology[C]//2015 34th Chinese Control Conference. Hang￾zhou, China, 2015: 6930−6935. [7] ZHAO L, JIA Y, YU J. Adaptive finite-time bipartite con￾sensus for second-order multi-agent systems with antagon￾istic interactions[J]. Systems & control letters, 2017, 102: 22–31. [8] LIN P, JIA Y. Consensus of a class of second-order multi￾agent systems with time-delay and jointly-connected topo￾logies[J]. IEEE transactions on automatic control, 2010, 55(3): 778–784. [9] 高玉兰, 于俊燕, 禹梅. 带有时滞的离散多智能体系统 的 H∞一致性问题 [J]. 系统科学与数学, 2015, 35(3): 317–326. GAO Yulan, YU Junyan, YU Mei. H∞. for discrete multi￾agent systems with time delay_[J]. Systems science and mathematics, 2015, 35(3): 317–326. [10] YU W, CHEN G, CAO M. Some necessary and suffi￾cient conditions for second-order consensus in multi￾agent dynamical systems[J]. Automatica, 2010, 46(6): 1089–1095. [11] LIU K, JI Z, REN W. Necessary and sufficient conditions for consensus of second-order multiagent systems under directed topologies without global gain dependency[J]. IEEE transactions on cybernetics, 2016, 47(8): [12] 第 4 期 冀秀坤，等：含时延约束的多智能体系统二分一致性 ·785·