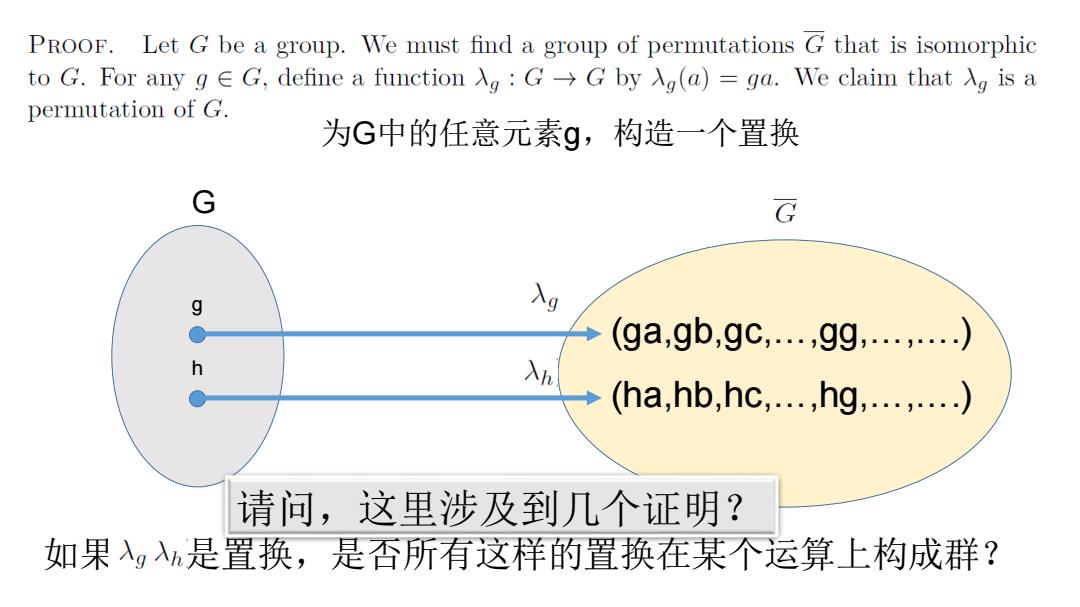
PROOF.Let G be a group.We must find a group of permutations G that is isomorphic toG.For any g∈G,define a functionλg:G→Gbyλg(a)=ga.W'e claim thatλgisa permutation of G. 为G中的任意元素g,构造一个置换 G G 入g (ga,gb,gc,…,gg,.….…） (ha,hb,hc,.,hg,.….) 请问，这里涉及到几个证明？ 如果λg是置换，是否所有这样的置换在某个运算上构成群？为G中的任意元素g，构造一个置换 G g (ga,gb,gc,…,gg,…,….) h (ha,hb,hc,…,hg,…,….) 如果 是置换，是否所有这样的置换在某个运算上构成群？ 请问，这里涉及到几个证明？