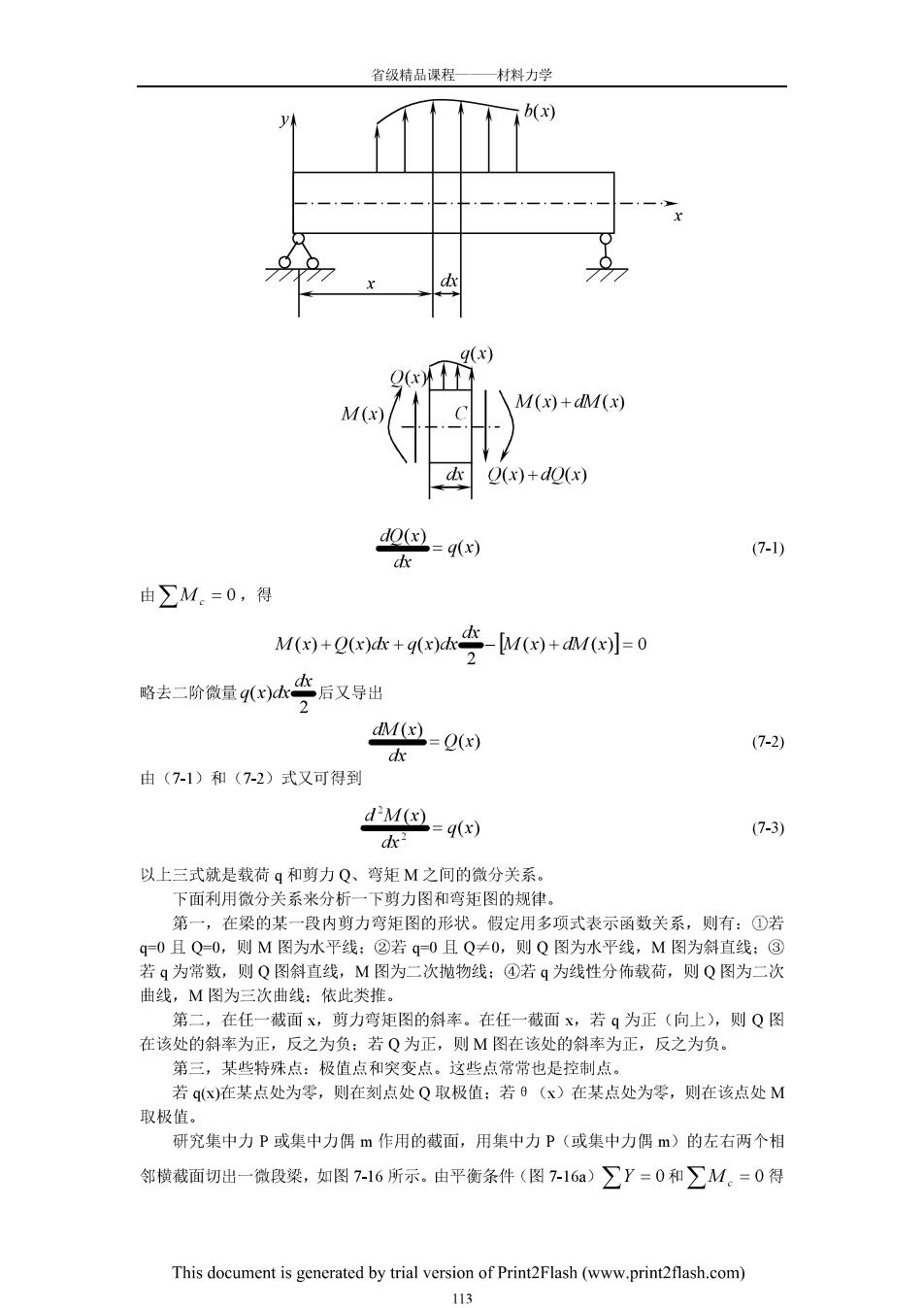
省领精品课程—材料力学 b(x) q(x) 2( M(x) \M()+dM(x) Q(x)+de(x) 7-1) 由∑M.=0,得 M+Qx达+qxh套M四+aM=0 略去二阶微量09k空后又导出 M(=0(x) (7-2) 由(7-1)和(7-2)式又可得到 dM因=4x) (7-3) ax- 以上三式就是载荷q和剪力Q、弯矩M之间的微分关系。 下面利用微分关系来分析一下剪力图和弯矩图的规律。 第一，在梁的某一段内剪力弯矩图的形状。假定用多项式表示函数关系，则有：①若 90且Q-0,则M图为水平线：②若q0且Q≠0，则Q图为水平线，M图为斜直线：@ 若q为常数，则Q图斜直线，M图为二次抛物线：④若q为线性分饰载荷，则Q图为二次 曲线，M图为三次曲线：依此类推。 第二，在任一截面x,剪力弯矩图的斜率。在任一裁面x,若q为正（向上），则Q图 在该处的斜率为正，反之为负：若Q为正，则M图在该处的斜率为正，反之为负。 第三，某些特殊点：极值点和突变点。这些点常常也是控制点。 若qx)在某点处为零，则在刻点处Q取极值：若0(x)在某点处为零，则在该点处M 取极 研究集中力P或集中力偶m作用的截面，用集中力P(或集中力偶m)的左右两个相 邻横截面切出一微段梁，如图7-16所示。由平衡条件（图-16a)∑Y=0和∑M。=0得 This document is generated by trial version of PrintFlash(www.printflash.com) 113