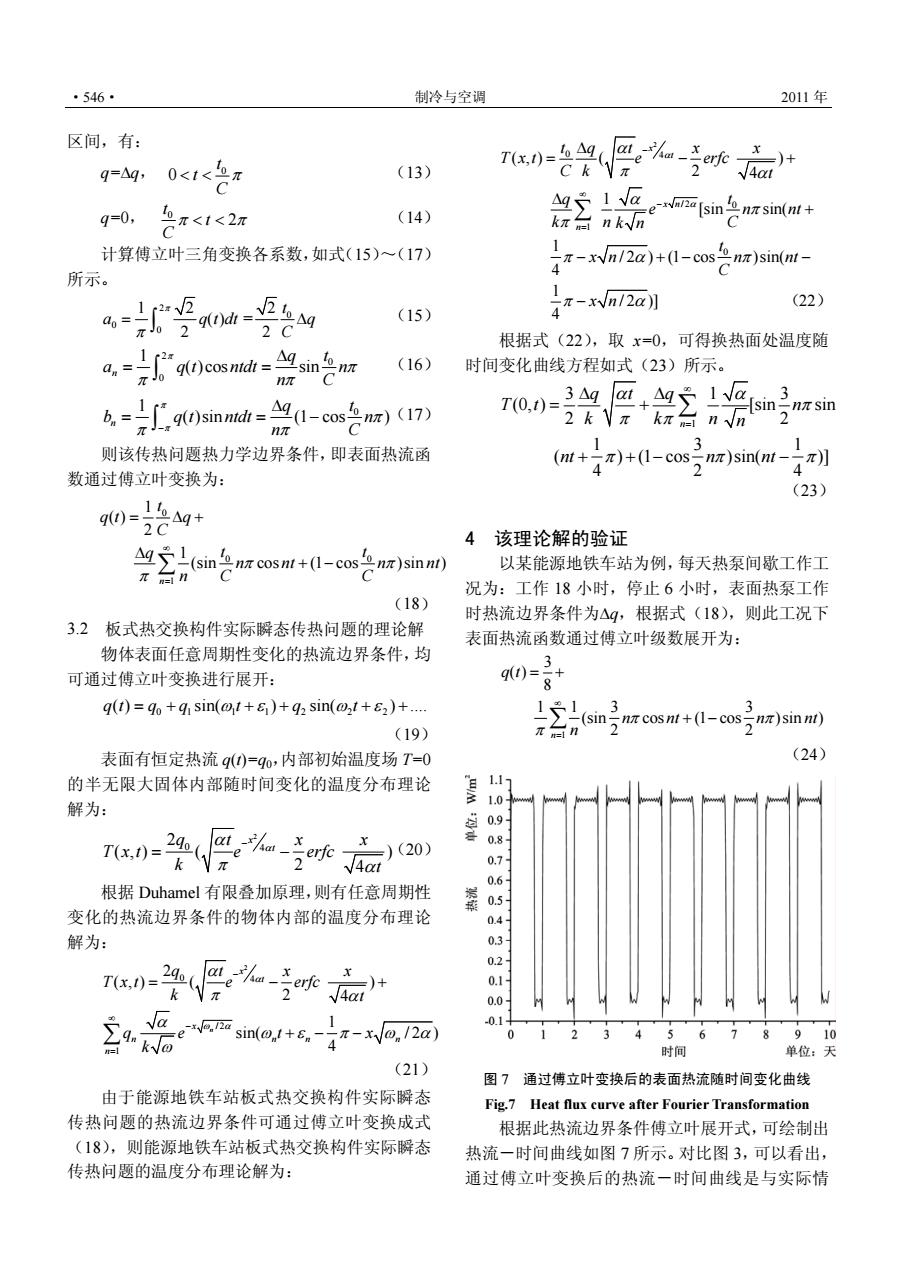
·546· 制冷与空调 2011年 区间，有： q=q,0<1<2π (13) q=0,π<1<2π (14) 2 enaa[sin会sin(nt+ 计算傅立叶三角变换各系数，如式(15)~(17) )+(cos)sin(nt- 所示。 4 x-xn12a) (22) (15) 根据式(22)，取x=0,可得换热面处温度随 a-片g0cast-岛m2 (16) 时间变化曲线方程如式(23)所示。 b()sinnd (-cos)(17) 则该传热问题热力学边界条件，即表面热流函 (n+(-cosnz)sin(n 数通过傅立叶变换为： (23) g0=是q+ 4 该理论解的验证 2cos1+0-o2jinm 以某能源地铁车站为例，每天热泵间歇工作工 况为：工作18小时，停止6小时，表面执泵工作 (18 时热流边界条件为△q,根据式(18)，则此工况下 3.2板式热交换构件实际解态传热问题的理论解 表面热流函数通过傅立叶级数展开为： 物体表面任意周期性变化的热流边界条件，均 可通过傅立叶变换进行展开： q(t)=qo+qisin(1+5)+q sin(@t+52)+.. (19) 表面有恒定热流g)=qo,内部初始温度场T=0 (24) 的半无限大固体内部随时间变化的温度分布理论 解为： 根据Duhamel有限叠加原理，则有任意周期性 .6 0 变化的热流边界条件的物体内部的温度分布理论 解为： 01- 品 sin() 678 时m (21) 图7通过傅立叶变换后的表面热流随时间变化曲线 由于能源地铁车站板式热交换构件实际瞬态 Fig.7 Heat flux curve after Fourier Transformation 传热问题的热流边界条件可通过傅立叶变换成式 根据此热流边界条件傅立叶展开式，可绘制出 (18),则能源地铁车站板式热交换构件实际瞬态 热流 时间曲线如图7所示。对比图3，可以看出 传热问题的温度分布理论解为： 通过傅立叶变换后的热流一时间曲线是与实际情 ·546· 制冷与空调 2011 年 区间，有： q=Δq， 0 0 t t C < < π （13） q=0， 0 2 t t C π < < π （14） 计算傅立叶三角变换各系数，如式（15）～（17） 所示。 2 0 0 0 12 2 () = 2 2 π π = Δ ∫ t a q t dt q C （15） 2 0 0 1 ( )cos sin π π π π Δ = = n ∫ q t a q t ntdt n n C （16） 0 1 ( )sin (1 cos ) π π π π π − Δ = =− n ∫ q t b q t ntdt n n C （17） 则该传热问题热力学边界条件，即表面热流函 数通过傅立叶变换为： 0 0 0 1 1 ( ) 2 1 (sin cos (1 cos )sin ) n t qt q C q t t n nt n nt nC C π π π ∞ = = Δ+ Δ ∑ + − （18） 3.2 板式热交换构件实际瞬态传热问题的理论解 物体表面任意周期性变化的热流边界条件，均 可通过傅立叶变换进行展开： 01 1 1 2 2 2 qt q q t q t ( ) sin( ) sin( ) .... =+ + + + + ω ε ωε （19） 表面有恒定热流 q(t)=q0，内部初始温度场 T=0 的半无限大固体内部随时间变化的温度分布理论 解为： 2 0 4 2 (,) ( ) 2 4 x t q t xx T x t e erfc k t α α π α − = − （20） 根据 Duhamel 有限叠加原理，则有任意周期性 变化的热流边界条件的物体内部的温度分布理论 解为： 2 0 4 / 2 1 2 (,) ( ) 2 4 1 sin( / 2 ) 4 n x t x n nn n n q t xx T x t e erfc k t qe t x k α ω α α π α α ω ε π ωα ω − ∞ − = = −+ ∑ +− − （21） 由于能源地铁车站板式热交换构件实际瞬态 传热问题的热流边界条件可通过傅立叶变换成式 （18），则能源地铁车站板式热交换构件实际瞬态 传热问题的温度分布理论解为： 2 0 4 / 2 0 1 0 (,) ( ) 2 4 1 [sin sin( 1 / 2 ) (1 cos )sin( 4 1 / 2 )] 22 4 x t x n n t qt x x T x t e erfc C k t q t e n nt kn C k n t x n n nt C x n α α α π α α π π πα π π α − ∞ − = Δ = −+ Δ + − +− − − ∑ （ ） 根据式（22），取 x=0，可得换热面处温度随 时间变化曲线方程如式（23）所示。 1 3 13 (0, ) [sin sin 2 2 131 ( ) (1 cos )sin( )] 424 n qt q Tt n k kn n nt n nt α α π π π π π π ∞ = Δ Δ = + + +− − ∑ （23） 4 该理论解的验证 以某能源地铁车站为例，每天热泵间歇工作工 况为：工作 18 小时，停止 6 小时，表面热泵工作 时热流边界条件为Δq，根据式（18），则此工况下 表面热流函数通过傅立叶级数展开为： 1 3 ( ) 8 11 3 3 (sin cos (1 cos )sin ) n 2 2 q t n nt n nt n π π π ∞ = = + ∑ + − （24） 图 7 通过傅立叶变换后的表面热流随时间变化曲线 Fig.7 Heat flux curve after Fourier Transformation 根据此热流边界条件傅立叶展开式，可绘制出 热流－时间曲线如图 7 所示。对比图 3，可以看出， 通过傅立叶变换后的热流－时间曲线是与实际情