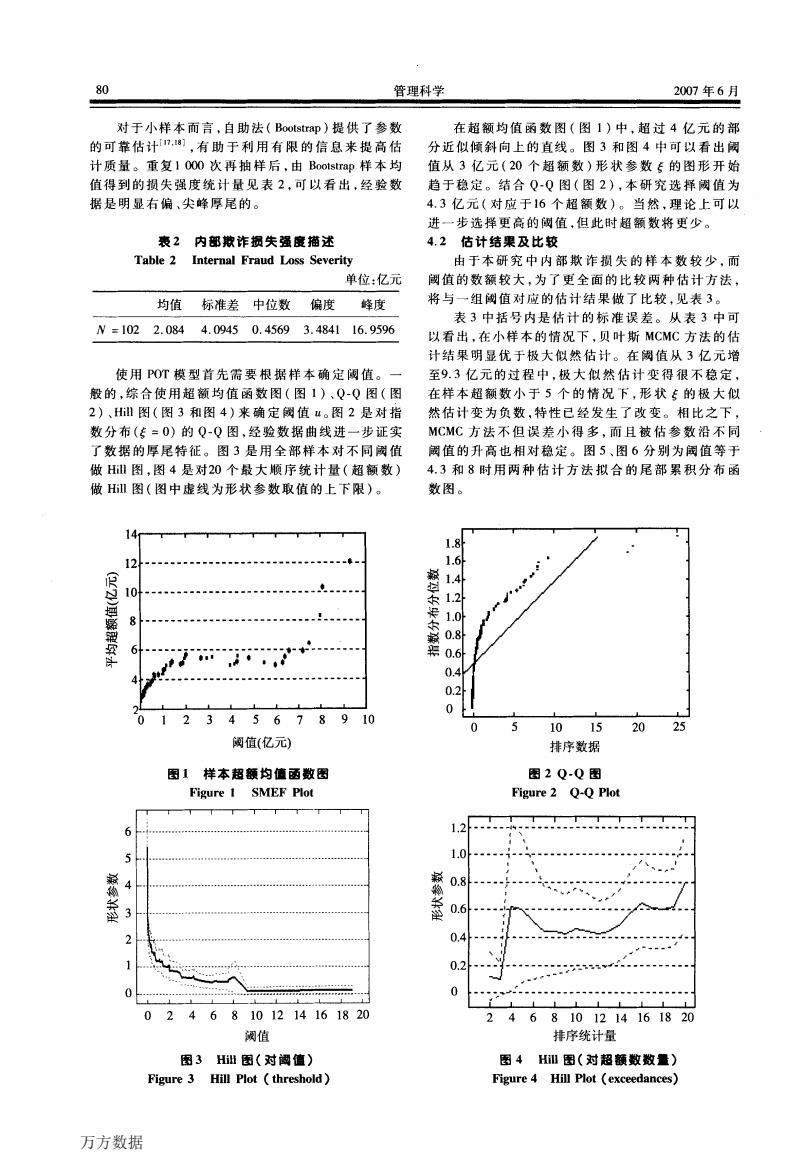
80 管理科学 2007年6月 对于小样本而言，自助法(Bootstra即)提供了参数 在超额均值函数图（图1）中，超过4亿元的部 的可靠估计.]，有助于利用有限的信息来提高估 分近似倾斜向上的直线。图3和图4中可以看出阀 计质量。重复】000次再抽样后，由Bootstrap样本均 值从3亿元(20个超额数)形状参数专的图形开始 值得到的损失强度统计量见表2，可以看出，经验数 趋于稳定。结合QQ图（图2），本研究选择阔值为 据是明显右偏、尖峰厚尾的。 4.3亿元（对应于16个超额数）。当然，理论上可以 进一步选择更高的阈值，但此时超额数将更少。 表2内部撒诈损失强度描述 4.2估计结果及比较 Table 2 Internal Fraud Loss Severity 由于本研究中内部欺诈损失的样本数较少，而 单位：亿元 阈值的数额较大，为了更全面的比较两种估计方法， 均值标准差中位数偏度 峰度 将与一组阈值对应的估计结果做了比较，见表3。 表3中括号内是估计的标准误差。从表3中可 N=1022.0844.09450.45693.484116.9596 以看出，在小样本的情况下，贝叶斯MCMC方法的估 计结果明显优于极大似然估计。在阅值从3亿元增 使用POT模型首先需要根据样本确定阀值。一 至9.3亿元的过程中，极大似然估计变得很不稳定， 般的，综合使用超额均值函数图（图1）、Q-Q图（图 在样本超额数小于5个的情况下，形状专的极大似 2)、Hl图（图3和图4）来确定镯值u。图2是对指 然估计变为负数，特性已经发生了改变。相比之下， 数分布（传=0）的Q-Q图，经验数据曲线进一步证实 MCMC方法不但误差小得多，而且被估参数沿不同 了数据的厚尾特征。图3是用全部样本对不同威值 值的升高也相对稳定。图5、图6分别为阈值等于 做H图，图4是对20个最大顺序统计量（超额数） 4.3和8时用两种估计方法拟合的尾部累积分布函 做H图（图中虚线为形状参数取值的上下限）。 数图。 14 1.8 12 1.6h 翰 1.4 10 1.2 8 1.0h 0.8 0.6 0.4 0.2 0 12345678910 1015 20 25 阅值（亿元） 排序数据 图1样本超额均值函数因 图2Q-Q图 Figure 1 SMEF Plot Figure 2 Q-Q Plot 1.2 10---1- 、 0.8 0.6 0.4 0.2 02468101214161820 68101214161820 阅值 排序统计量 图3Hi出图（对阁值） 图4H图（对超额数数量） Figure 3 Hill Plot threshold) Figure 4 Hill Plot (exceedances) 万方数据管理科学 2007年6月 对于小样本而言，自助法(Bootstrap)提供了参数 的可靠估计m，博1，有助于利用有限的信息来提高估 计质量。重复1 Ooo次再抽样后，由Bootstrap样本均 值得到的损失强度统计量见表2，可以看出，经验数 据是明显右偏、尖峰厚尾的。 表2内部欺诈损失强度描述 Table 2 Intemal F翰ud L0蟠SeVerity 单位：亿元 使用POT模型首先需要根据样本确定阈值。一 般的，综合使用超额均值函数图(图1)、Q—Q图(图 2)、Hin图(图3和图4)来确定阈值u。图2是对指 数分布(亭=0)的Q—Q图，经验数据曲线进一步证实 了数据的厚尾特征。图3是用全部样本对不同阈值 做Hill图，图4是对20个最大顺序统计量(超额数) 做Hill图(图中虚线为形状参数取值的上下限)。 1R 迥 埋 鞴 剐 蜜 鼬 6 5 慧4 垂s 2 1 O 阈值(亿元) 图1样本超额均值函数图 Figure l SMEF PlOt …辩． …．j±～：一 ，1- 、-．冬≮：：：：：：．：．人 、。‘～t。一．． ＼ …。‘’。“ 0 2 4 6 8 10 12 14 16 18 20 阈值 图3 Hill图(对阈值) Figure 3 Hm Plot(thr髂hom) 在超额均值函数图(图1)中，超过4亿元的部 分近似倾斜向上的直线。图3和图4中可以看出阈 值从3亿元(20个超额数)形状参数f的图形开始 趋于稳定。结合Q—Q图(图2)，本研究选择阈值为 4．3亿元(对应于16个超额数)。当然，理论上可以 进一步选择更高的阈值，但此时超额数将更少。 4．2估计结果及比较 由于本研究中内部欺诈损失的样本数较少，而 阈值的数额较大，为了更全面的比较两种估计方法， 将与一组阈值对应的估计结果做了比较，见表3。 表3中括号内是估计的标准误差。从表3中可 以看出，在小样本的情况下，贝叶斯MCMc方法的估 计结果明显优于极大似然估计。在阈值从3亿元增 至9．3亿元的过程中，极大似然估计变得很不稳定， 在样本超额数小于5个的情况下，形状f的极大似 然估计变为负数，特性已经发生了改变。相比之下， McMc方法不但误差小得多，而且被估参数沿不同 阈值的升高也相对稳定。图5、图6分别为阈值等于 4．3和8时用两种估计方法拟合的尾部累积分布函 数图。 籁 迥 求 挺 求 籁 避 籁 弧 篓 避 排序数据 图2 Q·Q图 ngure 2 Q·Q Plot 排序统计量 图4 Hm图(对超额数数量) Figure 4 HⅢPlot(exc∞dances) 万方数据