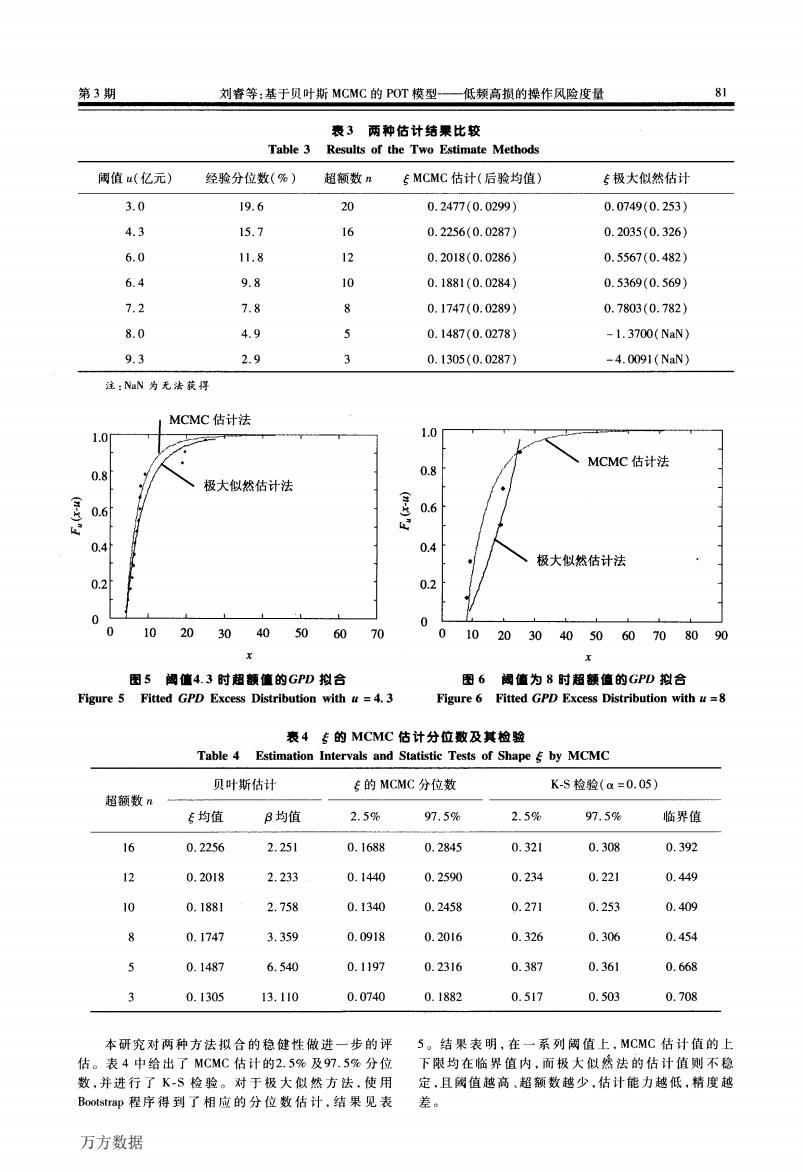
第3期 刘睿等：基于贝叶斯MCMC的POT模型—低频高损的操作风险度量 表3两种估计结聚比较 Table 3 Results of the Two Estimate Methods 阈值u(亿元) 经验分位数(%) 超额数n EMCMC估计（后验均值） 极大似然估计 3.0 19.6 20 0.2477(0.0299) 0.0749(0.253) 4.3 15.7 16 0.2256(0.0287） 0.2035(0.326) 6.0 11.8 12 0.2018(0.0286) 0.5567(0.482) 6.4 9.8 10 0.1881(0.0284) 0.5369(0.569) 7.2 7.8 8 0.1747(0.0289) 0.7803(0.782) 8.0 4.9 5 0.1487(0.0278) -1.3700(NaN) 9.3 2.9 3 0.1305(0.0287) -4.0091(NaN) 注：NaN为无法获得 MCMC估计法 1.0 1.0 MCMC估计法 0.8 0.8 极大似然估计法 0.6 0.6 0.4 0.4 极大似然估计法 0.2 0.2 0 0 102030405060 70 0 10 2030405060708090 x 图5阈值4.3时超额值的GPD拟合 图6阈值为8时超额值的GPD拟合 Figure 5 Fitted GPD Excess Distribution with u=4.3 Figure 6 Fitted GPD Excess Distribution with u=8 表4专的MCMC估计分位数及其检验 Table 4 Estimation Intervals and Statistic Tests of Shape by MCMC 贝叶斯估计 E的MCMC分位数 K-S检验(a=0.05) 超额数n 5均值 B均值 2.5% 97.5% 2.5% 97.5% 临界值 16 0.2256 2.251 0.1688 0.2845 0.321 0.308 0.392 12 0.2018 2.233 0.1440 0.2590 0.234 0.221 0.449 10 0.1881 2.758 0.1340 0.2458 0.271 0.253 0.409 0.1747 3.359 0.0918 0.2016 0.326 0.306 0.454 0.1487 6.540 0.1197 0.2316 0.387 0.361 0.668 3 0.1305 13.110 0.0740 0.1882 0.517 0.503 0.708 本研究对两种方法拟合的稳健性做进一步的评 5。结果表明，在一系列阑值上，MCMC估计值的上 估。表4中给出了MCMC估计的2.5%及97.5%分位 下限均在临界值内，而极大似然法的估计值则不稳 数，并进行了K-S检验。对于极大似然方法，使用 定，且阈值越高、超额数越少，估计能力越低，精度越 Bootstrap程序得到了相应的分位数估计，结果见表 差。 万方数据笙二墨2一．一． 型童箜：茎王!!竺±斯McMc的PoT模型——低频高损的操作风险度量 81 表3两种估讨结粟比较 Table 3 Results of the Two Estimate Methods ——————————————————————————————————————————————————一一 阈值M(亿元) 经验分位数(％) 超额数凡 fMcMc估计(后验均值) f极大似然估计 j-u 19·6 20 0．2477(0．0299) 0．0749(0．253) q‘j I，·7 16 0．2256(0．0287) 0．2035(0．326) 6．0 6．4 7．2 11．8 9．8 7．8 12 10 8 0．2018(0．0286) 0．5567(0．482) 0．188l(0．0284) 0．5369(0．569) 0．1747(0．0289) 0．7803(0．782) 8·O 4-9 5 O．1487(0．0278) 一1．3700(NaN) 9·3 2．9 3 O．1305(O．0287) 一4．009l(NaN) ———————————————————————————————————————————————一 注：NaN为无法获得 § 3 心 图5 阈值4．3时超额值的础D拟合 FigIlre 5 ntted船D Exce豁Distribution诮th“=4．3 § 6 心 X 图6 阈值为8时超额值的凹D拟合 Figure 6 Fitted G肋Excess Distmuti蛐with“=8 表4孝的McMc估计分位数及其检验 TabIe 4 Estimation Inter、，als and Statistic Tests of Shape f by MCMC ——————————————————————————————————————————————————————二_ 超额数n——～——————————————二——～一 ．。．． 贝叶斯估计 亭的McMc分位数 K．s检验(0【：O．05) 亭均值 卢均值 2．5％ 97．5％ 2．5％ 97．5％ 临界值 ———————————————————————————————————————————————————————————一 16 0．2256 2．25l 0．1688 0．2845 O．321 0．308 0．392 12 10 8 5 0．2018 0．188l 0．1747 0．1487 2．233 2．758 3．359 6．540 0．1440 0．1340 0．0918 0．1197 0．2590 0．2458 0．2016 0．2316 0．234 0．271 0．326 0．387 0．221 0．253 0．306 0．361 0．449 0．409 0．454 0．668 3 0．1305 13．110 0．0740 0．1882 0．517 0．503 0．708 ——————————————————————————————————————————————————————一 本研究对两种方法拟合的稳健性做进～步的评 估。表4中给出了MCMC估计的2．5％及97．5％分位 数，并进行了K—s检验。对于极大似然方法，使用 Bootstrap程序得到了相应的分位数估计，结果见表 5。结果表明，在一系列阈值上，McMc估计值的上 下限均在临界值内，而极大似然法的估计值则不稳 定，且阈值越高、超额数越少，估计能力越低，精度越 差。 万方数据