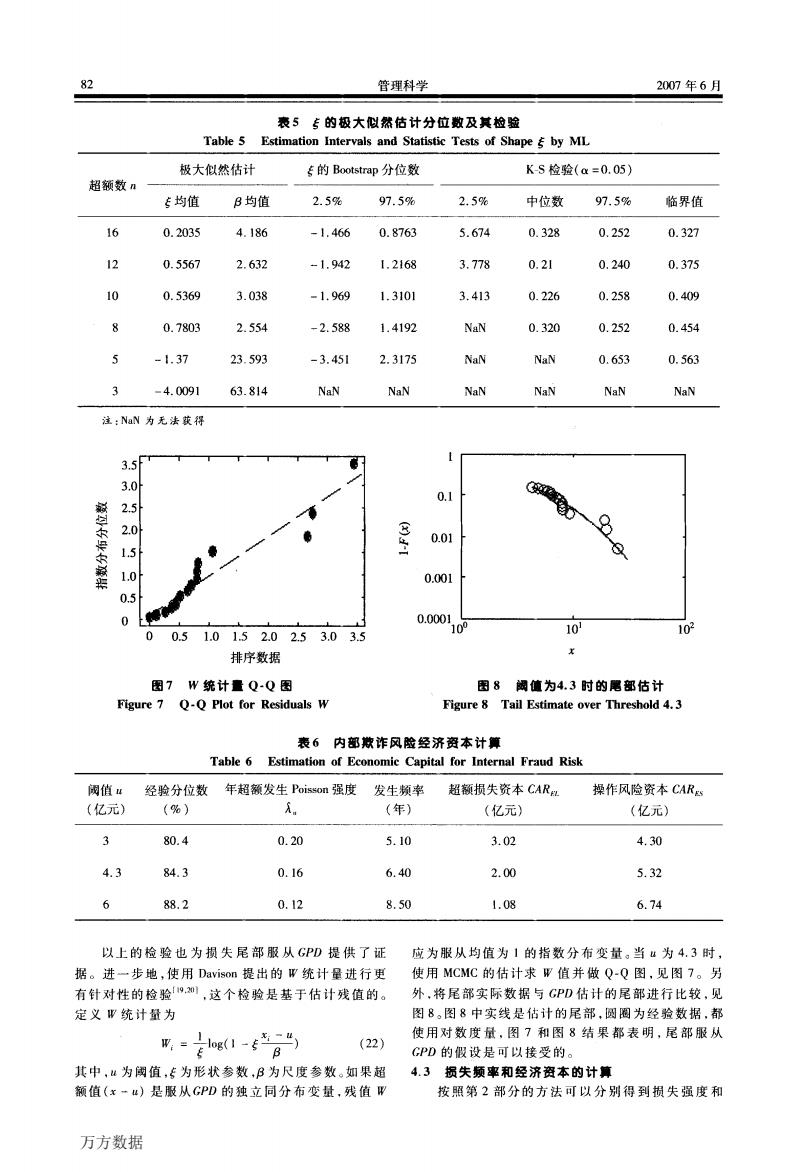
82 管理科学 2007年6月 表5专的极大似然估计分位数及其检验 Table 5 Estimation Intervals and Statistic Tests of Shape by ML 极大似然估计 专的Bootstrap分位数 KS检验(=0.05) 超额数n 专均值 B均值 2.5% 97.5% 2.5% 中位数 97.5% 临界值 16 0.2035 4.186 -1.466 0.8763 5.674 0.328 0.252 0.327 12 0.5567 2.632 -1.942 1.2168 3.778 0.21 0.240 0.375 10 0.5369 3.038 -1.969 1.3101 3.413 0.226 0.258 0.409 0.7803 2.554 -2.588 1.4192 NaN 0.320 0.252 0.454 5 -1.37 23.593 -3.451 2.3175 NaN NaN 0.653 0.563 -4.0091 63.814 NaN NaN NaN NaN NaN NaN 注：NaN为无法获得 3.5 3.0 0.1 0 2 8 0.01 1.0 0.001 0.5 0.000 10 00.51.01.52.02.53.03.5 10 102 排序数据 图7W统计置Q-Q图 图8锅值为4.3时的吧部估计 Figure 7 Q-O Plot for Residuals w Figure 8 Tail Estimate over Threshold 4.3 表6内部欺诈风险经济资本计算 Table 6 Estimation of Economic Capital for Internal Fraud Risk 阀值4 经验分位数 年超额发生Poisson强度 发生频率 超额损失资本CAR, 操作风险资本CARg (亿元) (%) A。 (年) (亿元) (亿元) 80.4 0.20 5.10 3.02 4.30 4.3 84.3 0.16 6.40 2.00 5.32 6 88.2 0.12 8.50 1.08 6.74 以上的检验也为损失尾部服从GPD提供了证 应为服从均值为1的指数分布变量。当u为4.3时， 据。进一步地，使用Davison提出的W统计量进行更 使用MCMC的估计求W值并做Q-Q图，见图7。另 有针对性的检验，，这个检验是基于估计残值的。 外，将尾部实际数据与GPD估计的尾部进行比较，见 定义W统计量为 图8。图8中实线是估计的尾部，圆圈为经验数据，都 属=e1-6角的) 使用对数度量，图7和图8结果都表明，尾部服从 (22) GPD的假设是可以接受的。 其中，“为阈值，专为形状参数，B为尺度参数。如果超 4.3损失频率和经济资本的计算 额值(x一u)是服从GPD的独立同分布变量，残值W 按照第2部分的方法可以分别得到损失强度和 万方数据82 管理科学 2007年6月 注：NaN为无法获得 籁 q 求 忙 求 籁 靼 排序数据 图7 w统计量Q·Q圈 Figure 7 Q-Q Hot for Residuals W S ‰ 二 图8 阈值为4．3时的尾部估计 Figure 8 Tail Estimate over Threshold 4．3 表6 内部欺诈风险经济资本计算 Table 6 Estimation of Econolllic Capital for Inter眦I Fraud硒sk 以上的检验也为损失尾部服从GPD提供了证 据。进一步地，使用Davison提出的形统计量进行更 有针对性的检验¨9’2…，这个检验是基于估计残值的。 定义形统计量为 1 z—H 阢2言109(1一f‘广) (22) 其中，H为阈值，f为形状参数，卢为尺度参数。如果超 额值(x一“)是服从GPD的独立同分布变量，残值形 应为服从均值为1的指数分布变量。当¨为4．3时， 使用McMc的估计求形值并做Q—Q图，见图7。另 外，将尾部实际数据与GPD估计的尾部进行比较，见 图8。图8中实线是估计的尾部，圆圈为经验数据，都 使用对数度量，图7和图8结果都表明，尾部服从 GPD的假设是可以接受的。 4．3损失频率和经济资本的计算 按照第2部分的方法可以分别得到损失强度和 万方数据