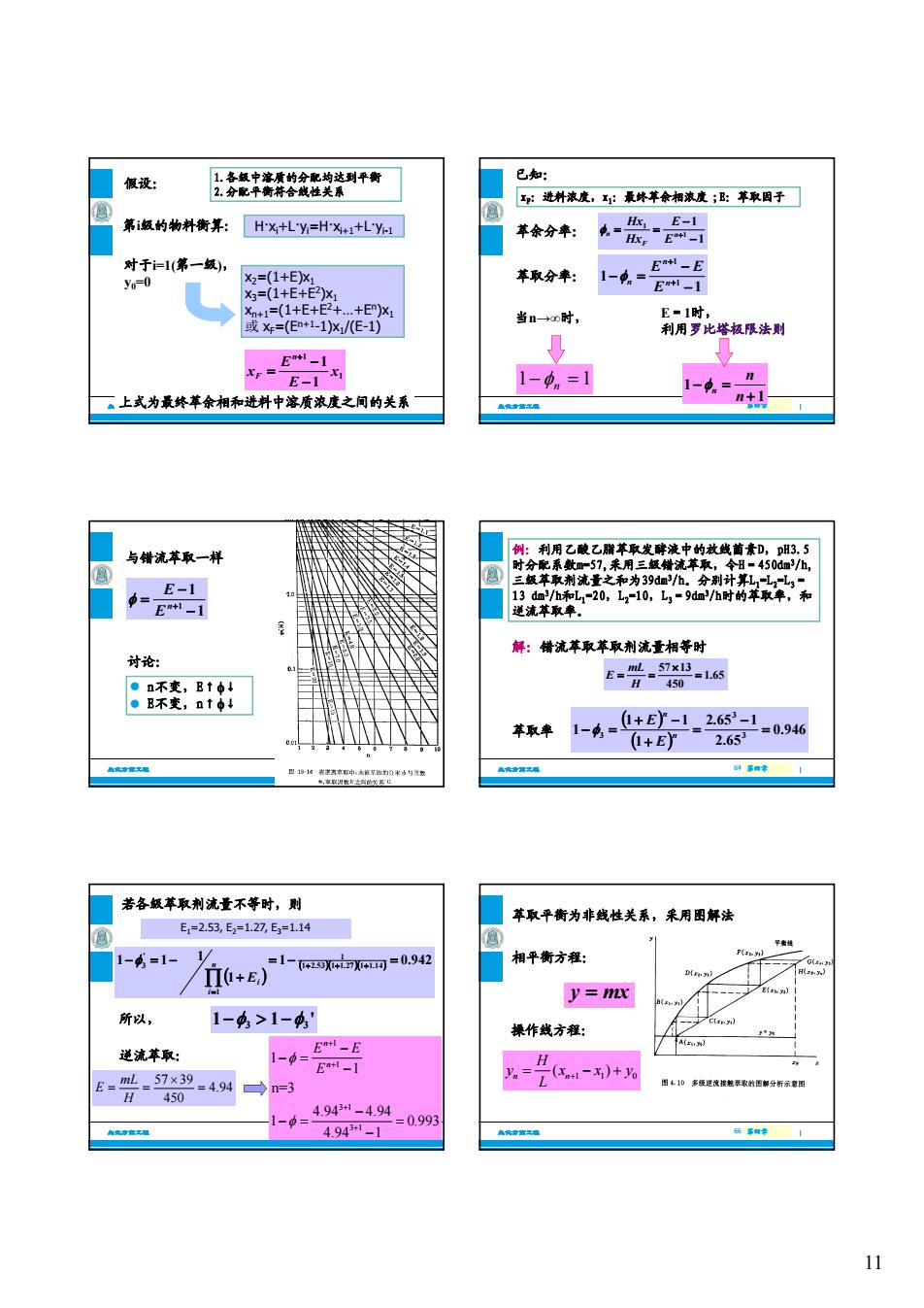
假设： 上持轻平补种在奖装有 第版的物料衡算：HX+Ly=HX1+L1 g- (2 萃取分率： 当n一时， 1-9n=1 一上或为最终草余相和进料中溶质浓度之间的关系 与错流萃取一样 E-1 B-1 解：错洗草取苹取剂花量相等时 讨论 E=-7-16的 8蹂r8 不44--2 (1+E 苦各级草取刺流香不等时，则 萃取平衡为非线性美系，来用图解法 1--1- h+E)1--g 相平衡方灌： y=mx 所以， 1-4>1-4 作幾方： 逆流革取： l_ 1-=E -贤-7”4→ .( 450 -0= 494m-4,94=0.993 4.941-1 11 11 1.各级中溶质的分配均达到平衡 2.分配平衡符合线性关系 H·xi +L·yi =H·xi+1+L·yi-1 x2=(1+E)x1 x (1+E+E2)x 假设： 第i级的物料衡算： 对于i=1(第一级)， y0=0 生化分离工程 第四章 第四章 | 61 x3=(1+E+E2)x1 xn+1=(1+E+E2+…+En)x1 或 xF=(En+1-1)x1/(E-1) 上式为最终萃余相和进料中溶质浓度之间的关系 1 1 1 1 x E E x n F     xF：进料浓度，x1：最终萃余相浓度 ;E：萃取因子 萃余分率： 1 1 1 1     n F n E E Hx Hx  萃取分率： 1 1 1 1       n n n E E E  已知： 生化分离工程 第四章 第四章 | E 1 当n→∞时， 1n  1 E＝1时， 利用罗比塔极限法则 1 1    n n  n 与错流萃取一样 1 1 1    n E E  生化分离工程 第四章 第四章 | 63  n不变，E↑↓  E不变，n↑↓ 讨论： 例：利用乙酸乙脂萃取发酵液中的放线菌素D，pH3.5 时分配系数m=57,采用三级错流萃取，令H＝450dm3/h, 三级萃取剂流量之和为39dm3/h。分别计算L1=L2=L3＝ 13 dm3/h和L1=20，L2=10，L3＝9dm3/h时的萃取率，和 逆流萃取率。 解：错流萃取萃取剂流量相等时 生化分离工程 第四章 第四章 | 64 1.65 450 57 13     H mL E     0.946 2.65 2.65 1 1 1 1 1 3 3 3         n n E E 萃取率  E1=2.53, E2=1.27, E3=1.14       1 0.942 1 1 1 1 1 2.53 1 1.27 1 1.14 1 1 ' 3             n i Ei  所以， 1   1  ' 若各级萃取剂流量不等时，则 生化分离工程 第四章 第四章 | 65 所以， 1 1 ' 3  3 逆流萃取： 4.94 450 57 39     H mL E 1 1 3 1 3 1 1 1 n=3 4.94 4.94 1 0.993 4.94 1 n n E E E               萃取平衡为非线性关系，采用图解法 相平衡方程： y  mx 生化分离工程 第四章 第四章 | 66 操作线方程： 11 0 ( ) n n H y x xy L    