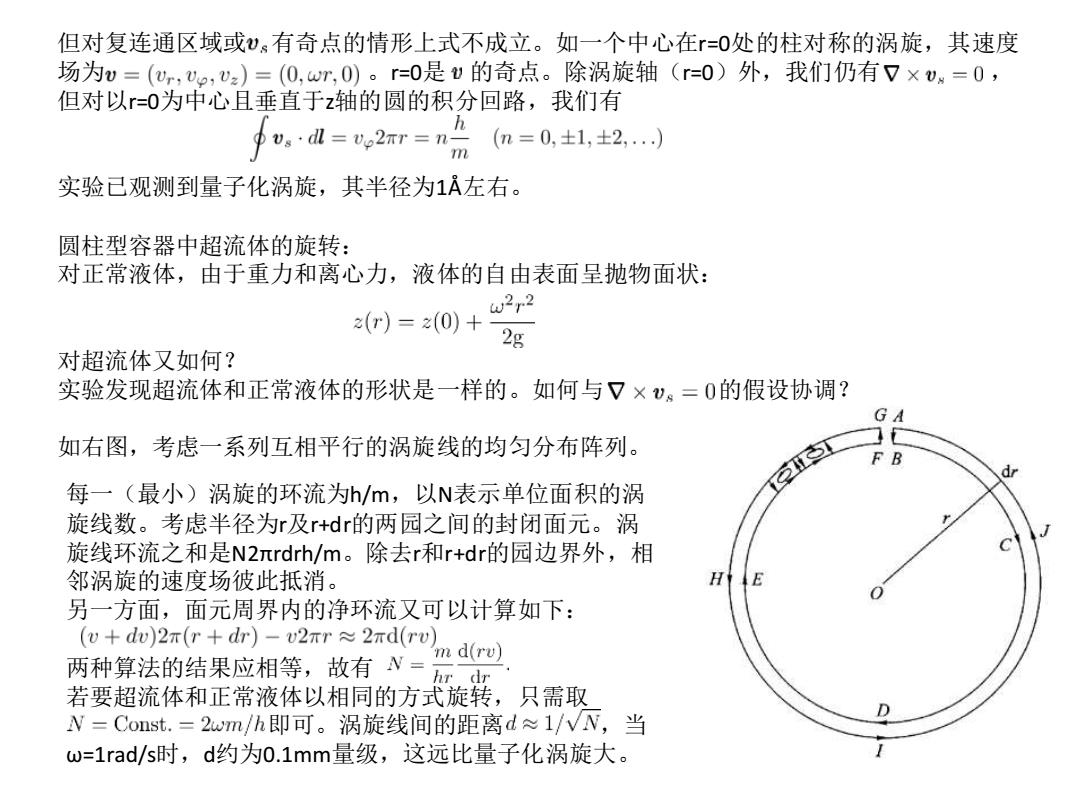
但对复连通区域或)。有奇点的情形上式不成立。如一个中心在r=0处的柱对称的涡旋，其速度 场为v=(ur,2,v2)=(0,wr,0)。r=0是v的奇点。除涡旋轴(r=0)外，我们仍有7×vw=0, 但对以=0为中心且垂直于z轴的圆的积分回路，我们有 udl=e2mr=n (n=0,土1，土2，..》 m 实验已观测到量子化涡旋，其半径为1A左右。 圆柱型容器中超流体的旋转： 对正常液体，由于重力和离心力，液体的自由表面呈抛物面状： w2r2 r)=20)+2g 对超流体又如何？ 实验发现超流体和正常液体的形状是一样的。如何与7×v。=0的假设协调？ 如右图，考虑一系列互相平行的涡旋线的均匀分布阵列。 每一（最小）涡旋的环流为h/m,以N表示单位面积的涡 旋线数。考虑半径为r及r+dr的两园之间的封闭面元。涡 旋线环流之和是N2πrdrh/m。除去r和r+dr的园边界外，相 邻涡旋的速度场彼此抵消。 H 另一方面，面元周界内的净环流又可以计算如下： (u+dw)2r(r+dr）-v2πr≈2πd(r 'm d(rv) 两种算法的结果应相等，故有V= hr dr 若要超流体和正常液体以相同的方式旋转，只需取 V=Const.=2wm/h即可。涡旋线间的距离d≈1/WW,当 w=1rad/s时，d约为0.1mm量级，这远比量子化涡旋大。但对复连通区域或 有奇点的情形上式不成立。如一个中心在r=0处的柱对称的涡旋，其速度 场为 。r=0是 的奇点。除涡旋轴（r=0）外，我们仍有 ， 但对以r=0为中心且垂直于z轴的圆的积分回路，我们有 实验已观测到量子化涡旋，其半径为1Å左右。 圆柱型容器中超流体的旋转： 对正常液体，由于重力和离心力，液体的自由表面呈抛物面状： 对超流体又如何？ 实验发现超流体和正常液体的形状是一样的。如何与 的假设协调？ 如右图，考虑一系列互相平行的涡旋线的均匀分布阵列。 每一（最小）涡旋的环流为h/m，以N表示单位面积的涡 旋线数。考虑半径为r及r+dr的两园之间的封闭面元。涡 旋线环流之和是N2πrdrh/m。除去r和r+dr的园边界外，相 邻涡旋的速度场彼此抵消。 另一方面，面元周界内的净环流又可以计算如下： 两种算法的结果应相等，故有 若要超流体和正常液体以相同的方式旋转，只需取 即可。涡旋线间的距离 ，当 ω=1rad/s时，d约为0.1mm量级，这远比量子化涡旋大