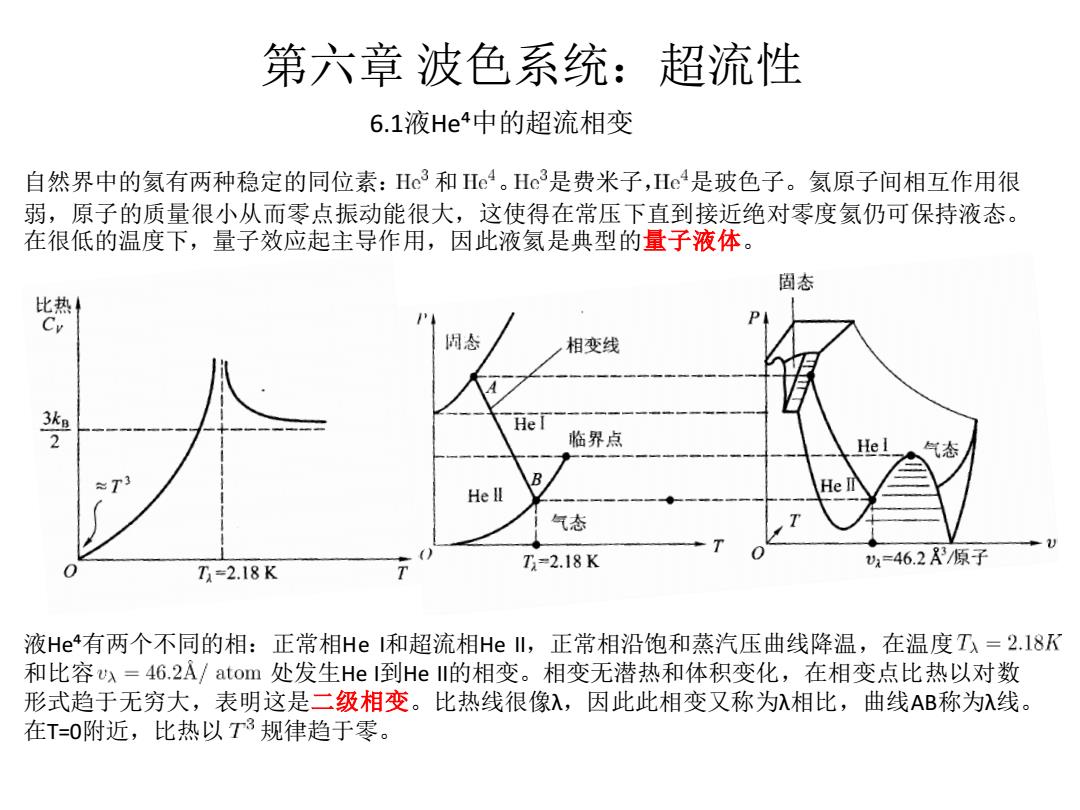
第六章波色系统:超流性 6.1液He4中的超流相变 自然界中的氦有两种稳定的同位素:Hc3和He4。Hc3是费米子,He4是玻色子。氦原子间相互作用很 弱,原子的质量很小从而零点振动能很大,这使得在常压下直到接近绝对零度氦仍可保持液态。 在很低的温度下,量子效应起主导作用,因此液氦是典型的量子液体。 固态 比热 闭态 相变线 HeI 临界点 气态 总T3 ⊙ Hell He 气态 U=46.2/原子 T=2.18K T=2.18K 液He4有两个不同的相:正常相He和超流相HeI,正常相沿饱和蒸汽压曲线降温,在温度T,=2.18K 和比容,=46.2A/atom处发生HeI到HeII的相变。相变无潜热和体积变化,在相变点比热以对数 形式趋于无穷大,表明这是二级相变。比热线很像入,因此此相变又称为λ相比,曲线AB称为λ线。 在T=0附近,比热以T规律趋于零
第六章 波色系统:超流性 6.1液He⁴中的超流相变 自然界中的氦有两种稳定的同位素: 和 。 是费米子, 是玻色子。氦原子间相互作用很 弱,原子的质量很小从而零点振动能很大,这使得在常压下直到接近绝对零度氦仍可保持液态。 在很低的温度下,量子效应起主导作用,因此液氦是典型的量子液体。 液He⁴有两个不同的相:正常相He I和超流相He II,正常相沿饱和蒸汽压曲线降温,在温度 和比容 处发生He I到He II的相变。相变无潜热和体积变化,在相变点比热以对数 形式趋于无穷大,表明这是二级相变。比热线很像λ,因此此相变又称为λ相比,曲线AB称为λ线。 在T=0附近,比热以 规律趋于零

6.2液HeI的特性二流体模型 液HeI的特性: 1.液HeⅡ能沿极细的毛细管流动而不呈现任何粘滞性,这称为超流性。而且存在一个临 界速度,在这个速度以上,超流性被破坏。 2. 如用一细丝悬挂一薄圆盘浸泡在液HeI里,并让圆盘作扭转振动,可以用来测粘滞系 数。结果比“毛细管”法测得的大106倍(与正常相的相似)。且测得的系数强烈依赖 于温度,随T→0K而趋于零。 3.当液HeI由容器A通过多孔塞(或极细的毛细管)流出时,A内液HeI的温度升高(见 右下图)。这称为机械热效应,其逆过程称为热机械效应。 4. 液HeI的热导率很大,数量级为室温下铜的800 倍,而且其热导与通常流体不同,并不正比于 温度梯度。 B 二流体模型的解释: 1.液HeI由正常流体和超流体两种成分组成。 连接的毛细管 超流体没有粘滞性,熵也为零;正常流体具 有粘滞性和熵,用Ps和Pm表示超流体和正常 流体的质量密度,速度场为)和v,则总质 T T+△T 量密度为:p=Ps十Pm,总质量流为: pV=psUg十Pnvn: 2.T=0K时,全液体为超流体;T=T时,全部为正常成分。二者之间时Psp是温度的函 数。 3.超流成分的速度场是无旋的,即又×v。=0。且两种流体成分可以相对流动而彼此间无 摩擦(无动量交换)
6.2 液He II的特性 二流体模型 液He II的特性: 1. 液He II能沿极细的毛细管流动而不呈现任何粘滞性,这称为超流性。而且存在一个临 界速度,在这个速度以上,超流性被破坏。 2. 如用一细丝悬挂一薄圆盘浸泡在液He II里,并让圆盘作扭转振动,可以用来测粘滞系 数。结果比“毛细管”法测得的大10⁶倍(与正常相的相似)。且测得的系数强烈依赖 于温度,随T→0K而趋于零。 3. 当液He II由容器A通过多孔塞(或极细的毛细管)流出时,A内液He II的温度升高(见 右下图)。这称为机械热效应,其逆过程称为热机械效应。 4. 液He II的热导率很大,数量级为室温下铜的800 倍,而且其热导与通常流体不同,并不正比于 温度梯度。 二流体模型的解释: 1. 液He II由正常流体和超流体两种成分组成。 超流体没有粘滞性,熵也为零;正常流体具 有粘滞性和熵,用 和 表示超流体和正常 流体的质量密度,速度场为 和 ,则总质 量密度为: ,总质量流为: 2. T=0K时,全部液体为超流体; 时,全部为正常成分。二者之间时 是温度的函 数。 3. 超流成分的速度场是无旋的,即 。且两种流体成分可以相对流动而彼此间无 摩擦(无动量交换)

只有超流成分可通过毛细管,这解释了特性一; 只有正常流体成分才对圆盘振动起阻尼作用,这解释了特性二: 机械制热效应:由毛细管流出的只是超流成分,不带走熵。因而容器内流体的单位质量 的熵将增加,导致温度增加。这解释了特性三; 特性四:设想均匀温度的液HeI中,某点附近温度突然稍稍上升。按二流体模型,热点 的P/p要增加,而Ps/P将减小,造成两种成分的密度涨落。为恢复平衡,热点附近的 超流成分将向热点流动,同时正常成分将向反方向流动而离开热点,这称作“内运流”。 这种内部调整进行的很快,使液HeI有极好的导热性。 由于液HeI中有两种成分,朗道预言4HeI中会有两种独立的振动波:若)s和Un方向一致, 测振动波传递密度和压强的变化,这是普通的声(第一声):若vs和)方向相反,则可能 在保持总密度p=Ps十P基本不变的情况下,Ps,Pm分别有涨落。由于超流成分熵为 零,P的涨落决定了熵密度的涨落和温度的涨落(如图所示)。 S,7
只有超流成分可通过毛细管,这解释了特性一; 只有正常流体成分才对圆盘振动起阻尼作用,这解释了特性二; 机械制热效应:由毛细管流出的只是超流成分,不带走熵。因而容器内流体的单位质量 的熵将增加,导致温度增加。这解释了特性三; 特性四:设想均匀温度的液He II中,某点附近温度突然稍稍上升。按二流体模型,热点 的 要增加,而 将减小,造成两种成分的密度涨落。为恢复平衡,热点附近的 超流成分将向热点流动,同时正常成分将向反方向流动而离开热点,这称作“内运流”。 这种内部调整进行的很快,使液He II有极好的导热性。 由于液He II中有两种成分,朗道预言He II中会有两种独立的振动波:若 和 方向一致, 则振动波传递密度和压强的变化,这是普通的声(第一声);若 和 方向相反,则可能 在保持总密度 基本不变的情况下, 分别有涨落。由于超流成分熵为 零, 的涨落决定了熵密度的涨落和温度的涨落(如图所示)

6.3超流体的涡旋运动 昂萨格和费因曼在理论上指出,在液HeI的基态或液HeI的超流成分中,可以存在一种“组 织化的运动”-量子化的涡旋。设N个玻色子组成的超流体的基态波函数为0,若液HeI相 以匀速)s运动,则系统波函数为: 这里ps=Nmws是超流体宏观运动的动量,R是质心坐标。若各粒子vs不均匀,在局部意义 上上式仍是一个较好的近似。即在比速度发生显著变化的距离小得多的范围内,由局部位 移引起的波函数的相位变化为: △功= vs·△rj 现在考虑超流体的涡旋。设想液H相中的一个闭合环,使环上每一原子从其原位置移到 其最近邻位置上。由于波函数的对称性,波函数不变。因此这种位移引起的波函数的相位 变化必为2π的整数倍,即 无∑△r)=2mn(m=0,士1,士2,) 注意求和只对环上的所有原子求和,对宏观尺度的闭合环,求和可换为积分: fu,dl=nhn=0,h,2小 这表明,环流是量子化的,环流量子为/m。由此可证超流成分的无旋性。由斯托克斯定理, ×u)ds=nm (n=0,±1,±2,… S为积分回路包围的曲面面积。若此区域是单连通的,且流速)。在S内处处连续,则左方的 积分可以随S连续地趋于零,但右方不能·连续变化,故只有7×va=0
6.3 超流体的涡旋运动 昂萨格和费因曼在理论上指出,在液He II的基态或液He II的超流成分中,可以存在一种“组 织化的运动”----量子化的涡旋。设N个玻色子组成的超流体的基态波函数为 ,若液He II相 以匀速 运动,则系统波函数为: 这里 是超流体宏观运动的动量,R是质心坐标。若各粒子 不均匀,在局部意义 上上式仍是一个较好的近似。即在比速度发生显著变化的距离小得多的范围内,由局部位 移引起的波函数的相位变化为: 现在考虑超流体的涡旋。设想液He II相中的一个闭合环,使环上每一原子从其原位置移到 其最近邻位置上。由于波函数的对称性,波函数不变。因此这种位移引起的波函数的相位 变化必为2π的整数倍,即 注意求和只对环上的所有原子求和,对宏观尺度的闭合环,求和可换为积分: 这表明,环流是量子化的,环流量子为h/m。由此可证超流成分的无旋性。由斯托克斯定理, S为积分回路包围的曲面面积。若此区域是单连通的,且流速 在S内处处连续,则左方的 积分可以随S连续地趋于零,但右方不能·连续变化,故只有
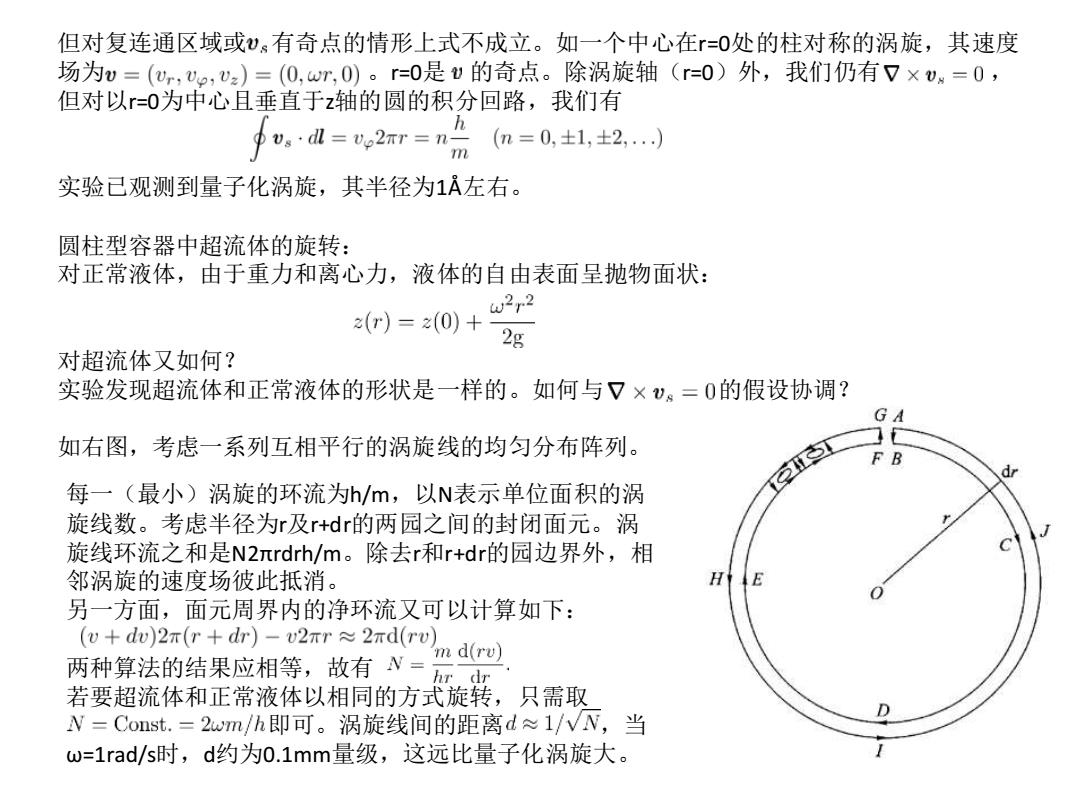
但对复连通区域或)。有奇点的情形上式不成立。如一个中心在r=0处的柱对称的涡旋,其速度 场为v=(ur,2,v2)=(0,wr,0)。r=0是v的奇点。除涡旋轴(r=0)外,我们仍有7×vw=0, 但对以=0为中心且垂直于z轴的圆的积分回路,我们有 udl=e2mr=n (n=0,土1,土2,..》 m 实验已观测到量子化涡旋,其半径为1A左右。 圆柱型容器中超流体的旋转: 对正常液体,由于重力和离心力,液体的自由表面呈抛物面状: w2r2 r)=20)+2g 对超流体又如何? 实验发现超流体和正常液体的形状是一样的。如何与7×v。=0的假设协调? 如右图,考虑一系列互相平行的涡旋线的均匀分布阵列。 每一(最小)涡旋的环流为h/m,以N表示单位面积的涡 旋线数。考虑半径为r及r+dr的两园之间的封闭面元。涡 旋线环流之和是N2πrdrh/m。除去r和r+dr的园边界外,相 邻涡旋的速度场彼此抵消。 H 另一方面,面元周界内的净环流又可以计算如下: (u+dw)2r(r+dr)-v2πr≈2πd(r 'm d(rv) 两种算法的结果应相等,故有V= hr dr 若要超流体和正常液体以相同的方式旋转,只需取 V=Const.=2wm/h即可。涡旋线间的距离d≈1/WW,当 w=1rad/s时,d约为0.1mm量级,这远比量子化涡旋大
但对复连通区域或 有奇点的情形上式不成立。如一个中心在r=0处的柱对称的涡旋,其速度 场为 。r=0是 的奇点。除涡旋轴(r=0)外,我们仍有 , 但对以r=0为中心且垂直于z轴的圆的积分回路,我们有 实验已观测到量子化涡旋,其半径为1Å左右。 圆柱型容器中超流体的旋转: 对正常液体,由于重力和离心力,液体的自由表面呈抛物面状: 对超流体又如何? 实验发现超流体和正常液体的形状是一样的。如何与 的假设协调? 如右图,考虑一系列互相平行的涡旋线的均匀分布阵列。 每一(最小)涡旋的环流为h/m,以N表示单位面积的涡 旋线数。考虑半径为r及r+dr的两园之间的封闭面元。涡 旋线环流之和是N2πrdrh/m。除去r和r+dr的园边界外,相 邻涡旋的速度场彼此抵消。 另一方面,面元周界内的净环流又可以计算如下: 两种算法的结果应相等,故有 若要超流体和正常液体以相同的方式旋转,只需取 即可。涡旋线间的距离 ,当 ω=1rad/s时,d约为0.1mm量级,这远比量子化涡旋大

6.4朗道超流理论 朗道理论的基本图像是把液HeI看成受弱激发的量子波色系统,弱激发态与基态(T=OK)的偏离 表现为在安稳的背景上出现了由元激发或准粒子组成的气体,后者与二流体模型中的正常液 体成分对应,而前者代表超流成分(回忆上章最后一节的另一个例子)。 当温度很低时,元激发的密度很低,可以把它们看作元激发的理想气体。令p和(P)代表元激 发的动量和能量,(p)表示相应的元激发数,则系统低激发态的总能量和动量为: E=Eo+n(p)e(p),P=>pn(p). p 朗道进一步假设液HeI中存在两种不同的波色型元激发(准粒子),即声子和旋子。当T《T 时,液HeI的比热随T3变化,这是声子的特征,其能谱为e=cp,c为声子速度。当温度稍高时, 比热有一如exp[△/kT]的附加项,其中△为常数。由此推测对较大的动量,元激发能量有一个 能隙,朗道假定在这个动量范围内能谱为: E(p) p=k=△+p-=△+ 方2(k-ko)2 2m* 2m* m是旋子的有效质量。 声子谱 旋子谱 热力学性质: 这里准粒子被看作是理想波色气体,准粒子数目不 确定,系统的化学势为零。准粒子在能量wk的平均占 据数为:(mx)=1/(e疏w-1), Po 由此可得内能:U=Eo+∑kx)=Bo+2x。 d k2hwk 和定容比热Cv
6.4 朗道超流理论 朗道理论的基本图像是把液He II看成受弱激发的量子波色系统,弱激发态与基态(T=0K)的偏离 表现为在安稳的背景上出现了由元激发或准粒子组成的气体,后者与二流体模型中的正常液 体成分对应,而前者代表超流成分(回忆上章最后一节的另一个例子)。 当温度很低时,元激发的密度很低,可以把它们看作元激发的理想气体。令 和 代表元激 发的动量和能量, 表示相应的元激发数,则系统低激发态的总能量和动量为: 朗道进一步假设液He II中存在两种不同的波色型元激发(准粒子),即声子和旋子。当 时,液He II的比热随 变化,这是声子的特征,其能谱为ε=cp,c为声子速度。当温度稍高时, 比热有一如exp[-Δ/kBT]的附加项,其中Δ为常数。由此推测对较大的动量,元激发能量有一个 能隙,朗道假定在这个动量范围内能谱为: 是旋子的有效质量。 热力学性质: 这里准粒子被看作是理想波色气体,准粒子数目不 确定,系统的化学势为零。准粒子在能量 的平均占 据数为: 由此可得内能: 和定容比热

因此声子部分贡献的比热为:Cphonon 2n2v(kBT)3 NkB 15(hc)3 旋子贡献的比热在假设kBT/△为小量时,可得 Croton_2Vm*(ka△)2ve-△/kn7 NkB h(2TkBT)3/2 这些结果与实验符合的很好。 超流的临界速度(T=O)小: 设质量为M的超流体以宏观速度运动,其动量和能量为: P=M,E=M2- p2 2M 因此动量和能量的任何变化必满足:6E=·P 设这一变化是由超流体产生了一个新的元激发引起,其动量为P,能量为(p)。 按能量和动量守恒,元激发的动量和能量必由消耗超流体的宏观流动的动量和能量而来,故 p=-6P,e(p)=-6E 因此我们有e(p)=v·p≤vp或v≥e(p)/p. 上式说明,要能产生元激发,必须超流体的宏观流速大于e(P)/p;反之对一切小于e(p)/p的v 值,则由于宏观流动而产生新的元激发是不可能的,即流体继续保持超流。由此得到超流判 据: E(p) 三Uc min ,即为超流的临界速度。由此易知自由粒子能谱:切)=云不可能有超流,因 =0
因此声子部分贡献的比热为: 旋子贡献的比热在假设 为小量时,可得 这些结果与实验符合的很好。 超流的临界速度(T=0): 设质量为M的超流体以宏观速度v运动,其动量和能量为: 因此动量和能量的任何变化必满足: 设这一变化是由超流体产生了一个新的元激发引起,其动量为 ,能量为 。 按能量和动量守恒,元激发的动量和能量必由消耗超流体的宏观流动的动量和能量而来,故 因此我们有 或 上式说明,要能产生元激发,必须超流体的宏观流速大于 ;反之对一切小于 的v 值,则由于宏观流动而产生新的元激发是不可能的,即流体继续保持超流。由此得到超流判 据: 即为超流的临界速度。由此易知自由粒子能谱 不可能有超流,因

6.5简并性近理想波色气体 波戈留波夫变换 这里我们用一个简并型近理想波色气体模型来来微观地给出液He的声子能谱。 近理想气体是稀薄的(即密度低),相互作用很弱(可以看作微扰)的粒子系统。此外我 们仅考虑系统的低温性质,这时量子效应很明显。几个相关参数: ·散射长度a,它反映相互作用势的强度和作用范围; ·平均热波长入T,它代表粒子波包的平均空间范围,属于量子效应,低温时入T可以很大: ·粒子间平均距离:l心n-1/3(n为气体密度)。 我们假定这三个参数间有如下关系(L为容器线度): a《λT;a《;λT≈l《L. 因此相互作用可以按小量a/入r展开。 哈密顿量及其简化: 设近理想波色气体由N个全同的,自旋为零的波色子组成,系统哈密顿量为: 自-立器+∑a0,-r0=角+ 述,上式可写为 pipalup2)apppp P1P2P1 P2 其中第二式的求和要满足动量守恒条件,,及,分别为动量为p的单粒子态的产生和湮灭算 符,它们满足波色算符的对易关系:[ap,a]=dpp,[ap,ap]=[a站,a]=0. 相互作用矩阵元为,叫1p,P四=ordraj.()(ra)(r1-ra9n.e9n 其中m)=。P"是动量为p的单粒子态的波函数
6.5简并性近理想波色气体 波戈留波夫变换 这里我们用一个简并型近理想波色气体模型来来微观地给出液He II的声子能谱。 近理想气体是稀薄的(即密度低),相互作用很弱(可以看作微扰)的粒子系统。此外我 们仅考虑系统的低温性质,这时量子效应很明显。几个相关参数: • 散射长度a,它反映相互作用势的强度和作用范围; • 平均热波长 ,它代表粒子波包的平均空间范围,属于量子效应,低温时 可以很大; • 粒子间平均距离: (n为气体密度)。 我们假定这三个参数间有如下关系(L为容器线度): 因此相互作用可以按小量 展开。 哈密顿量及其简化: 设近理想波色气体由N个全同的,自旋为零的波色子组成,系统哈密顿量为: 采用二次量子化表述,上式可写为: 其中第二式的求和要满足动量守恒条件, 及 分别为动量为p的单粒子态的产生和湮灭算 符,它们满足波色算符的对易关系: 相互作用矩阵元为 其中 是动量为p的单粒子态的波函数

把波函数表达式代入即可得,p必lp,p2)=arer/hr。 这里p=p1-p1=P2-p2,T=T1-T2 在低湿下,由量子力学低能散射的波恩近似,对散射长度我们有:a=深, 在低能散射下,动量转移p很小,可取近似epr)/h≈1。因此 a≈ dru(r)= muo 4r2 p,pip1,p2)≈. 因此体系的哈密顿量可写为:自=∑时,+品 再进一步,我们可以考虑波戈留波夫近似,即和0近似地代之以C数(可交换数)N,而且 由于我们只考虑低激发态,有: No/N≈1,Np/N<1(p≠0). 因此站和a,(p≠0)可看作小量,我们只保留到二次项,而略去三次及以上的高阶小量。故 p≠0 其中a站a站aga0≈N哈≈N2-2N∑站ap, P≠0 二次项的六项近似为o(a时a过p+pa-p+4时ap)≈N(a站过p+ini-p+4i站ap). 因此哈密倾量最终近似为:自-∑品0++工时的,+,+时) 2V+2V p≠0
把波函数表达式代入即可得 这里 在低温下,由量子力学低能散射的波恩近似,对散射长度a我们有: 在低能散射下,动量转移p很小,可取近似 。因此 因此体系的哈密顿量可写为: 再进一步,我们可以考虑波戈留波夫近似,即 和 近似地代之以C数(可交换数) 而且 由于我们只考虑低激发态,有: 因此 和 可看作小量,我们只保留到二次项,而略去三次及以上的高阶小量。故 其中 二次项的六项近似为 因此哈密顿量最终近似为:

波戈留波夫变换: 类似上章末节,我们可以通过波戈留波夫变换来把哈密顿量严格对角化。 引入新的波色产生和湮灭算符,和bp: i站=upi站-na-p,bp=pp-nap 其中4,和p为两个待定参数,常取为实数,且2=u-p,p=”-p:可以验证若令哈-哈=1则 和b,满足波色对易关系(注意这两个参数还有一个自由度)。上式的逆变换为: a站=n站+pb-p,ap=unip+nb过p 带入到哈密顿量表达式中得 月= +∑{(+)+}+{(+)++}, {(品+)+”G+}(达,+4)】 我们可取两个待定参数的值使得:(二+停),+”(兮+)=0则上式最后一项为零, 哈密顿量被对角化。 解出参数的值可得:p= Up 其中: V1- V1-昭 4πi2aN\ 1/2 Lp mu2 m2V o=+()门 m, 从上面u和e(p)的结果我们发现,如果散射长度a<0,u为虚数,从而对某些动量P的元 激发可使()为虚数,这是粒子间存在吸引作用不可能产生波色-爱因斯坦凝聚的原因
波戈留波夫变换: 类似上章末节,我们可以通过波戈留波夫变换来把哈密顿量严格对角化。 引入新的波色产生和湮灭算符 和 : 其中 和 为两个待定参数,常取为实数,且 可以验证若令 则 和 满足波色对易关系(注意这两个参数还有一个自由度)。上式的逆变换为: 带入到哈密顿量表达式中得 我们可取两个待定参数的值使得: 则上式最后一项为零, 哈密顿量被对角化。 解出参数的值可得: 其中: 从上面u和 的结果我们发现,如果散射长度a<0,u为虚数,从而对某些动量 的元 激发可使 为虚数,这是粒子间存在吸引作用不可能产生波色-爱因斯坦凝聚的原因