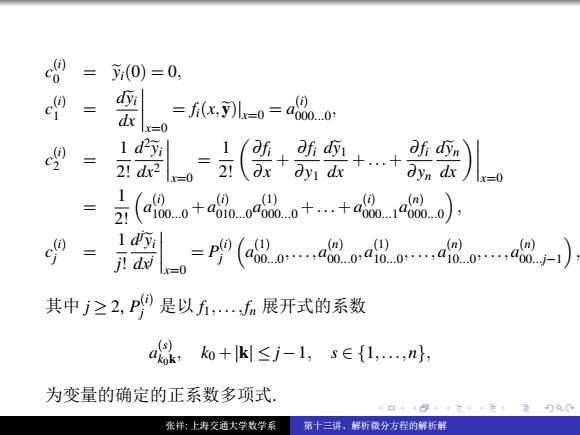
= (0)=0, = d =xl=o=a品。0 x=0 1d2 1 2!dr2 2（a+ ay dx 元（a8o.0+a90.060.0+.+am.14m0.0p (1) () (n) I dyi d▣ =p9(a80…,8oa80,a80…,8- (n) =0 其中j≥2，p9是以f,n展开式的系数 ko+k≤j-1,s∈{1，.，n} 为变量的确定的正系数多项式. 张样：上海交通大学数学系 第十三讲、解析微分方程的解折解 c (i) 0 = eyi(0) = 0, c (i) 1 = deyi dx     x=0 = fi(x,ey)| x=0 = a (i) 000...0 , c (i) 2 = 1 2! d 2eyi dx2     x=0 = 1 2!  ∂ fi ∂ x + ∂ fi ∂ y1 dey1 dx +...+ ∂ fi ∂ yn deyn dx     x=0 = 1 2!  a (i) 100...0 +a (i) 010...0 a (1) 000...0 +...+a (i) 000...1 a (n) 000...0  , c (i) j = 1 j! d jeyi dxj     x=0 = P (i) j  a (1) 00...0 ,...,a (n) 00...0 ,a (1) 10...0 ,...,a (n) 10...0 ,...,a (n) 00...j−1  , Ÿ• j ≥ 2, P (i) j ¥± f1,...,fn –m™XÍ a (s) k0k , k0 +|k| ≤ j−1, s ∈ {1,...,n}, èC˛(½XÍıë™. ‹å: ˛°œåÆÍÆX 1õn˘!)¤á©êß)¤)