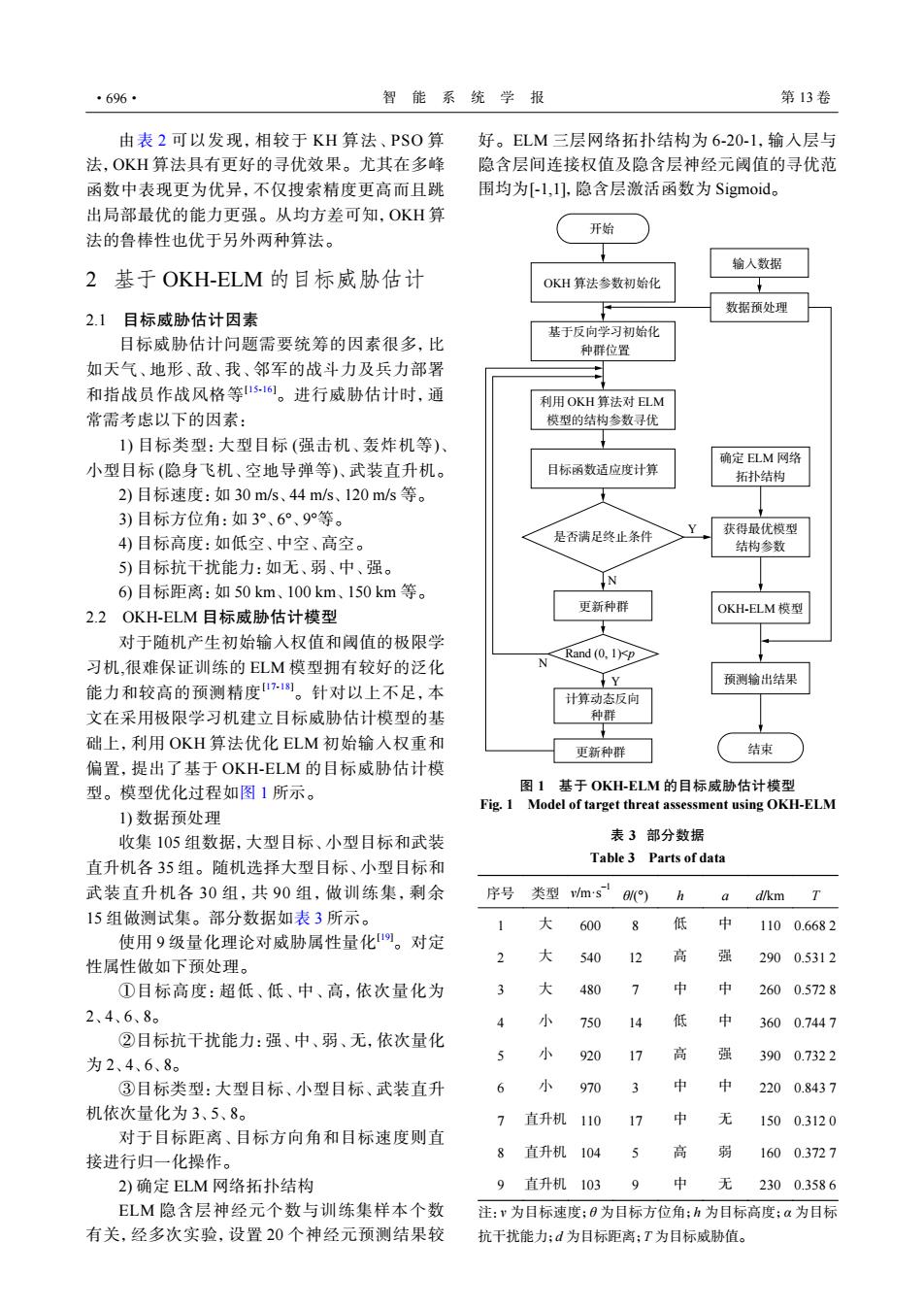
·696· 智能系统学报 第13卷 由表2可以发现，相较于KH算法、PSO算 好。ELM三层网络拓扑结构为6-20-1，输入层与 法，OKH算法具有更好的寻优效果。尤其在多峰 隐含层间连接权值及隐含层神经元阈值的寻优范 函数中表现更为优异，不仅搜索精度更高而且跳 围均为[-l,1],隐含层激活函数为Sigmoid.。 出局部最优的能力更强。从均方差可知，OKH算 法的鲁棒性也优于另外两种算法。 开始 输人数据 2基于OKH-ELM的目标威胁估计 OKH算法参数初始化 数据预处理 2.1目标威胁估计因素 基于反向学习初始化 目标威胁估计问题需要统筹的因素很多，比 种群位置 如天气、地形、敌、我、邻军的战斗力及兵力部署 和指战员作战风格等us161。进行威胁估计时，通 利用OKH算法对ELM 常需考虑以下的因素： 模型的结构参数寻优 1)目标类型：大型目标（强击机、轰炸机等）、 确定ELM网络 小型目标（隐身飞机、空地导弹等）、武装直升机。 目标函数适应度计算 拓扑结构 2)目标速度：如30m/s、44m/s、120m/s等。 3)目标方位角：如3°、6°、9°等。 获得最优模型 4)目标高度：如低空、中空、高空。 是否满足终止条件 结构参数 5)目标抗干扰能力：如无、弱、中、强。 6)目标距离：如50km、100km、150km等。 IN 更新种群 OKH-ELM模型 2.2OKH-ELM目标威胁估计模型 对于随机产生初始输入权值和阈值的极限学 Rand (0,1)<p 习机，很难保证训练的ELM模型拥有较好的泛化 Y 预测输出结果 能力和较高的预测精度1。针对以上不足，本 计算动态反向 文在采用极限学习机建立目标威胁估计模型的基 种群 础上，利用OKH算法优化ELM初始输入权重和 更新种群 结束 偏置，提出了基于OKH-ELM的目标威胁估计模 型。模型优化过程如图1所示。 图1基于OKH-ELM的目标威胁估计模型 Fig.1 Model of target threat assessment using OKH-ELM 1)数据预处理 收集105组数据，大型目标、小型目标和武装 表3部分数据 直升机各35组。随机选择大型目标、小型目标和 Table 3 Parts of data 武装直升机各30组，共90组，做训练集，剩余 序号 类型vms(o) h a d/km 15组做测试集。部分数据如表3所示。 大 600 8 低 1100.6682 使用9级量化理论对威胁属性量化。对定 2 大 性属性做如下预处理。 540 12 高 强 2900.5312 ①目标高度：超低、低、中、高，依次量化为 3 大 480 2600.5728 2、4、6、8。 750 3600.7447 ②目标抗干扰能力：强、中、弱、无，依次量化 5 92 为2、4、6、8。 3900.7322 ③目标类型：大型目标、小型目标、武装直升 6 小 970 3 中 2200.8437 机依次量化为3、5、8。 7 直升机110 17 中 无 1500.3120 对于目标距离、目标方向角和目标速度则直 接进行归一化操作。 8 直升机104 5 高 象 1600.3727 2)确定ELM网络拓扑结构 9直升机103 9 中 无 2300.3586 ELM隐含层神经元个数与训练集样本个数 注：v为目标速度：0为目标方位角：h为目标高度：a为目标 有关，经多次实验，设置20个神经元预测结果较 抗干扰能力；d为目标距离：T为目标威胁值。由表 2 可以发现，相较于 KH 算法、PSO 算 法，OKH 算法具有更好的寻优效果。尤其在多峰 函数中表现更为优异，不仅搜索精度更高而且跳 出局部最优的能力更强。从均方差可知，OKH 算 法的鲁棒性也优于另外两种算法。 2 基于 OKH-ELM 的目标威胁估计 2.1 目标威胁估计因素 目标威胁估计问题需要统筹的因素很多，比 如天气、地形、敌、我、邻军的战斗力及兵力部署 和指战员作战风格等[15-16]。进行威胁估计时，通 常需考虑以下的因素： 1) 目标类型：大型目标 (强击机、轰炸机等)、 小型目标 (隐身飞机、空地导弹等)、武装直升机。 2) 目标速度：如 30 m/s、44 m/s、120 m/s 等。 3) 目标方位角：如 3°、6°、9°等。 4) 目标高度：如低空、中空、高空。 5) 目标抗干扰能力：如无、弱、中、强。 6) 目标距离：如 50 km、100 km、150 km 等。 2.2 OKH-ELM 目标威胁估计模型 对于随机产生初始输入权值和阈值的极限学 习机,很难保证训练的 ELM 模型拥有较好的泛化 能力和较高的预测精度[17-18]。针对以上不足，本 文在采用极限学习机建立目标威胁估计模型的基 础上，利用 OKH 算法优化 ELM 初始输入权重和 偏置，提出了基于 OKH-ELM 的目标威胁估计模 型。模型优化过程如图 1 所示。 1) 数据预处理 收集 105 组数据，大型目标、小型目标和武装 直升机各 35 组。随机选择大型目标、小型目标和 武装直升机各 30 组 ，共 90 组，做训练集，剩余 15 组做测试集。部分数据如表 3 所示。 使用 9 级量化理论对威胁属性量化[19]。对定 性属性做如下预处理。 ①目标高度：超低、低、中、高，依次量化为 2、4、6、8。 ②目标抗干扰能力：强、中、弱、无，依次量化 为 2、4、6、8。 ③目标类型：大型目标、小型目标、武装直升 机依次量化为 3、5、8。 对于目标距离、目标方向角和目标速度则直 接进行归一化操作。 2) 确定 ELM 网络拓扑结构 ELM 隐含层神经元个数与训练集样本个数 有关，经多次实验，设置 20 个神经元预测结果较 好。ELM 三层网络拓扑结构为 6-20-1，输入层与 隐含层间连接权值及隐含层神经元阈值的寻优范 围均为[-1,1]，隐含层激活函数为 Sigmoid。 OKH 算法参数初始化 确定 ELM 网络 拓扑结构 输入数据 数据预处理 基于反向学习初始化 种群位置 利用 OKH 算法对 ELM 模型的结构参数寻优 目标函数适应度计算 是否满足终止条件 获得最优模型 结构参数 OKH-ELM 模型 结束 开始 更新种群 Rand (0, 1)<p 计算动态反向 种群 更新种群 Y N Y N 预测输出结果 图 1 基于 OKH-ELM 的目标威胁估计模型 Fig. 1 Model of target threat assessment using OKH-ELM 表 3 部分数据 Table 3 Parts of data 序号 类型 v/m·s–1 θ/(°) h a d/km T 1 大 600 8 低 中 110 0.668 2 2 大 540 12 高 强 290 0.531 2 3 大 480 7 中 中 260 0.572 8 4 小 750 14 低 中 360 0.744 7 5 小 920 17 高 强 390 0.732 2 6 小 970 3 中 中 220 0.843 7 7 直升机 110 17 中 无 150 0.312 0 8 直升机 104 5 高 弱 160 0.372 7 9 直升机 103 9 中 无 230 0.358 6 注：v 为目标速度；θ 为目标方位角；h 为目标高度；α 为目标 抗干扰能力；d 为目标距离；T 为目标威胁值。 ·696· 智 能 系 统 学 报 第 13 卷