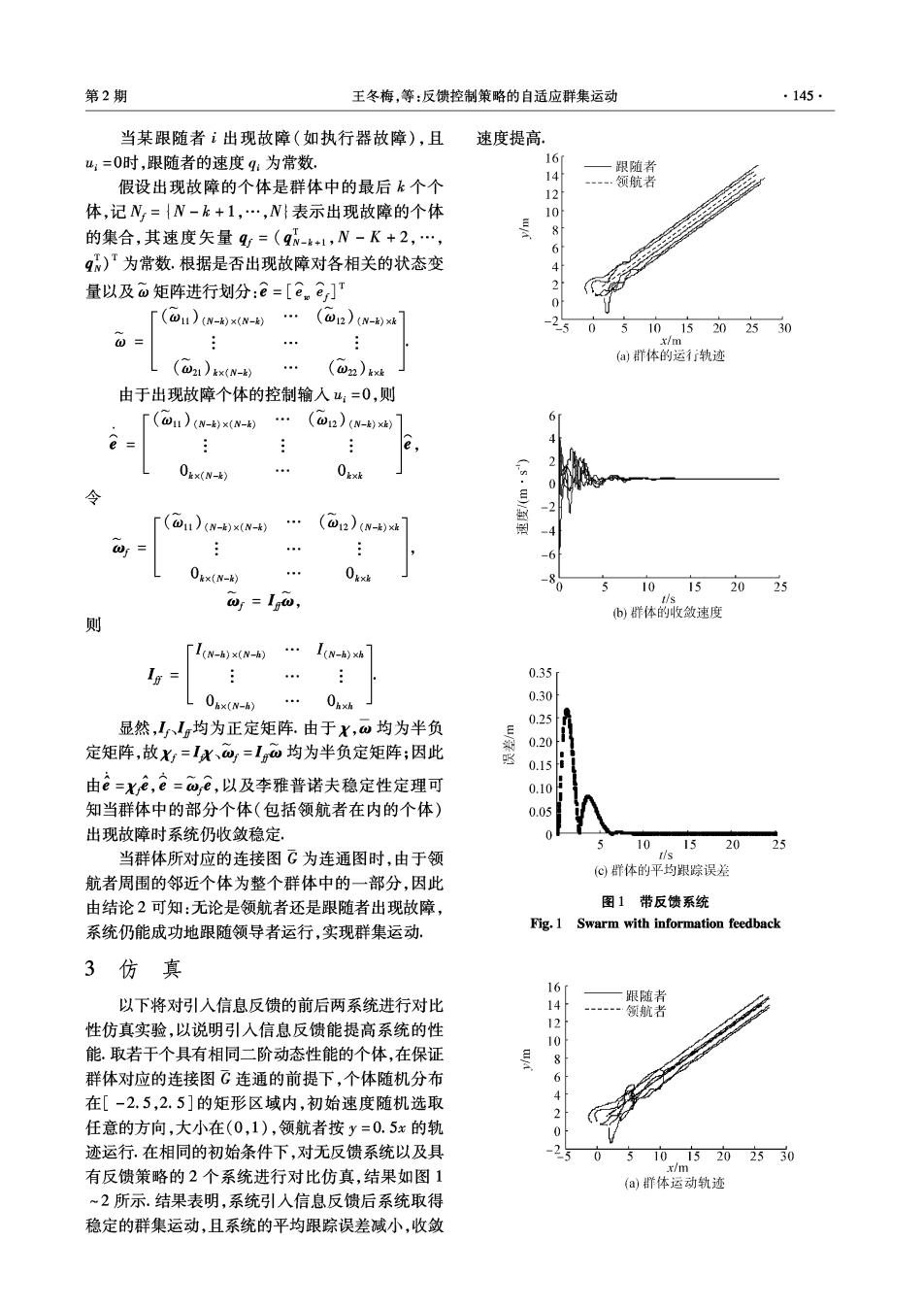
第2期 王冬梅，等：反馈控制策略的自适应群集运动 ·145 当某跟随者i出现故障（如执行器故障），且 速度提高， 4:=0时，跟随者的速度q:为常数. 16 跟随者 14 假设出现故障的个体是群体中的最后k个个 -…领航者 12 体，记N={N-k+1,…,W}表示出现故障的个体 10 的集合，其速度矢量q=（qN-k+1,N-K+2,…, 8 6 q)T为常数.根据是否出现故障对各相关的状态变 量以及0矩阵进行划分：e=[ene]T 3 厂(01i)(w-kx(N-·(®12）(w-X 25 0 51015202530 0 x/m (a)群体的运轨迹 (@2)kx(N-) (@)kxk 由于出现故障个体的控制输入山：=0，则 「(d1)w-xN-…(o2)- @ e ix(N-) Oixk 风 2 r(011)(w-)x(N-k) (012)(N-k)x =4 Ox(N-k) … Oxxck 5 10 1520 25 ws Igw, t/s b)群体的收敛速度 则 I(N-h)x(N-h) I(N-h)xh 0.35 Opx(N-) Oxk 0.30 显然，I、Ig均为正定矩阵.由于K,w均为半负 0.25 0.20 定矩阵，故X=IX、@=I0均为半负定矩阵；因此 驱 0.15 由e=Xe,e=0,e,以及李雅普诺夫稳定性定理可 0.10 知当群体中的部分个体（包括领航者在内的个体） 0.05 出现故障时系统仍收敛稳定， 1520 10 25 当群体所对应的连接图G为连通图时，由于领 (©群体的平均跟踪误差 航者周围的邻近个体为整个群体中的一部分，因此 由结论2可知：无论是领航者还是跟随者出现故障， 图1带反馈系统 系统仍能成功地跟随领导者运行，实现群集运动， Fig.1 Swarm with information feedback 3仿真 16 跟随者 以下将对引入信息反馈的前后两系统进行对比 14 领航者 性仿真实验，以说明引人信息反馈能提高系统的性 12 10 能。取若干个具有相同二阶动态性能的个体，在保证 群体对应的连接图C连通的前提下，个体随机分布 6 在[-2.5,2.5]的矩形区域内，初始速度随机选取 2 任意的方向，大小在(0,1)，领航者按y=0.5x的轨 0 迹运行.在相同的初始条件下，对无反馈系统以及具 0 510.15202530 x/m 有反馈策略的2个系统进行对比仿真，结果如图1 (a)群体运动轨迹 ~2所示.结果表明，系统引入信息反馈后系统取得 稳定的群集运动，且系统的平均跟踪误差减小，收敛