
第6卷第2期 智能系统学报 Vol.6 No.2 2011年4月 CAAI Transactions on Intelligent Systems Apr.2011 doi:10.3969/i.issn.1673-4785.2011.02.008 反馈控制策略的自适应群集运动 王冬梅,方华京2 (1.武汉科技大学信息科学与工程学院,湖北武汉430081;2.华中科技大学控制科学与工程系,湖北武汉430074) 摘要:针对有领航者的多智能体群集运动中可能出现的跟踪误差大或跟随者掉队的现象,提出了一种基于信息反 馈的自适应的群集运动跟踪方法.采用邻近规则在领航者与周围邻近的跟随者之间引入双向信息流,使得领航者按 事先确定的轨迹运行的同时,能根据邻近的跟随者的状态信息自适应地调节自身的运行状态.并采用李亚普诺夫方 法分析了系统的稳定性,证明了该策略能诚小系统的跟踪误差且对系统的机械故障和网络故障具有鲁棒性.仿真结 果证明了该控制策略能提高系统的性能. 关键词:多智能体系统;群集运动;信息反馈;协调控制 中图分类号:TP13文献标识码:A文章编号:16734785(2011)02014106 An adaptive flocking motion with a leader based on a feedback control scheme WANG Dongmei,FANG Huajing? (1.College of Information Science and Engineering,Wuhan University of Science and Technology,Wuhan 430081,China;2.Depart- ment of Control Seience and Engineering,Huazhong University of Science and Technology,Wuhan 430074,China) Abstract:An adaptive flocking motion with information feedback was presentd for a leader-following approach in a multi-Agent system.This system may have large errors or the phenomenon of the follower falling behind.By intro- ducing two information flows between the leader and its local neighbors,the leader can track a pre-defined trajecto- ry,and at the same time,can modify its motion according to the static information of the neighboring followers.The Lyapunov approach was used to analyze the stability of the system and demonstrate that the strategy of information feedback can decrease the tracing errors and improve the robustness of the system for overcoming mechanical and network malfunctions.The results of the simulations were given to illustrate that information feedback can improve the performance of the system. Keywords:multi-Agent system;flocking motion;information feedback;cooperative control 近年来,多智能群体的群集运动控制问题引起了实际领航者的群集运动控制问题,文献[8]以移动的 研究人员的极大关注.这主要是由于多智能体系统在参考点作为虚拟领航者实现群集运动,文献[9-12]采 生物、物理以及工程等多个领域的广泛应用31,如在用虚拟领航者跟随者结构研究分析了群集运动,其 军事和工业领域中的多智能体协调控制、无人机 中文献[11-12]研究了带多个虚拟领航者的群集运动 (UAVS)协调控制、多机器人编队控制、分布式传感器 控制问题.但上述文献均没有探讨利用反馈机制修正 网络等问题.多智能体的研究主要集中于设计合适的 调节领航者的运行,领航者与跟随者之间无直接的反 控制协议和算法使得系统取得不同形式的协调一致 馈.其缺点在于:首先,当领航者以时变速度运行时, 性.通过采用图论和其他的一些方法,研究者研究了 跟随者将不能保持较小的跟随误差,准确地跟随期望 许多有趣的协调问题,其中带领航者群体的协调控制 轨迹运行,甚至跟踪失败:其次,领航者与跟随者之间 是研究主题之一.文献[47]采用邻近规则研究了带 是单向连接,领航者易受到攻击,缺乏鲁棒性.另一方 面,当跟随者受到干扰,由于领航者不能根据跟随者 收稿日期:2010-05-11. 基金项目:国家自然科学基金资助项目(60574088,60874053):湖北 的信息调节自身运行状态,跟踪效率将受到极大的影 省教育厅资助项目(Q20101105). 响,使得群体跟踪理想轨迹更加困难.目前存在一种 通信作者:王冬梅.E-mail:wdmyou@126.com. 从跟随者到领航者的队形反馈机制34,整个队形被

·142 智能系统学报 第6卷 看成一个虚拟结构,在该结构中每个个体有着对应的 或者领航者的不平稳的运行速度,群集运行过程中 理想位置,个体的实际位置与对应理想位置之差作为 往往存在跟踪误差.为了减小群体的跟踪误差,需要 队形误差,以此作为反馈误差来协调整个群体以固定 引入反馈机制来调节领航者的运行状态.如当领航 的队形运行.该策略中整个群体需要以严格确定的队 者相对于跟随者运行太快或太慢时,领航者能实时 形运行,其应用范围受到了极大的限制.文献[15]初 根据邻近跟随者的信息调节自身的状态,使跟随者 步研究了在领航者跟随者引入反馈策略并定性地分 不出现掉队或拥挤现象,从而使群体整体协调的按 析了系统的性能.本文在文献[15]的基础上继续探讨 理想轨迹运行. 如何将反馈机制融合到领航者跟随者协调控制过程 鉴于此,本文通过引入反馈机制在领航者与其 中,并分析了系统的鲁棒性和容错性能, 邻近的个体间建立双向信息流,使领航者跟随理想 轨迹运行的同时也受其邻近个体的状态影响.领航 1 有领航者的群集运动控制 者将根据理想轨迹和邻近个体的运行状态自适应的 考虑由一个领航者和N个跟随者组成的群体, 调节自身运行状态,从而使整个群体的运行达到协 跟随者的动态方程为 调一致 p:=9:,9:=4,i=1,2,…,N. (1) 90=f(p0,90,pj,41), 式中:P:∈Rn表示个体的位置;q:∈Rn表示速度向 46=-[(po-p6)+y(qo-q6)]- 量;4:∈Rm表示控制输入.领航者的动态方程为 [∑(p-p)+y∑(9-g)]. (3) je N N。 P0=9o,90=fP0,9o). (2) 式中:y>0,r为常数,(p,4)为领航者的邻近个体j 式中:Po∈Rm表示个体的位置;qo∈Rm表示速度向 的状态.(P,96)为对应时刻的理想轨迹的状态, 量:f(po,9o)表示领航者的控制输人,领航者的状态 假设只有部分个体与领航者相连接,连接图G 是时变的, 连通且不变.下列等式将产生群集运动, 定义1邻接图G(V,e(p))表示个体间相互 跟随者的控制律为 作用及通讯关系,其中:V={no,n1,…,nw}表示顶 点集,由N个个体组成;e(p)={(n:,n)∈V×}表 4,=-74g+∑g(g-g)+ jeNi jeNt 示边集,由个体间的邻接关系确定.若从n:到乃有 h:(t)[90-1(p:-po)-c2(9:-qo)].(4) 一条路径,则称n:和n是连通的.若G(V,e(p))中 式中:中:为与个体间的相对距离相关的势能函数, 任意2个不同的顶点:和都是连通的(即有路 径),则称G为连通图. 女,=(P,-p,只.A,()=1,当跟随者在领航者的 图C表示群体中所有个体间的相互作用及通 感知范围内时;否则,h:(t)=0, 讯关系,由2部分组成:一部分是无向图G,表示跟 2主要结论与系统性能分析 随者间通过无向边相连接;另一部分表示领航者与 跟随者间通过有向边相连接.当图G为连通图,且 引入反馈策略,领航者将根据周围环境信息 图G中至少有一个跟随者与领航者通过有向边相 (邻近个体的状态)自适应的调节自身状态,引导整 连接时,则图G是连通的. 个群体按事先确定的理想轨迹运行,形成稳定的群 集合N△{Uj)~i表示跟随者i的邻居集,A= 集运动, [ag],其中am=0,ag=a%>0(i,j=1,2,…,n)jeN 2.1稳定性分析 表示无向图G的邻接矩阵;集合N。表示领航者的 考虑一个领航者和N个个体组成的群体,假设 邻居集,其中b:=an,b:表示个体与领航者间的连接 群体所对应的邻接图G为连通图,领航者与跟随者 权重.当个体i在领航者的感知范围内时,b:>0,否 的动态方程由式(1)、(2)描述,运动控制律由式 则b=0. (3)、(4)描述,那么整个群体将按事先确定的理想 定义2群集运动.在智能群体中如果所有个 轨迹运行,且最终形成稳定的群集运动. 体取得相同的速度向量,且两两之间的距离稳定不 证明首先考虑领航者,令P。=P0一p6,90= 发生碰撞,就称群体渐近地取得群集运动. q。-g6,q。=o,式(3)可化简为 带领航者的群集运动是指所有个体(包括领航 90=-[p0+y9o]- 者和跟随者)彼此间以稳定的间距按事先给定的轨 迹跟随领航者以稳定的速度运行.但由于外界干扰 A。-)+yX-)1. jeN

第2期 王冬梅,等:反馈控制策略的自适应群集运动 ·143· A 则取能量函数:V,=Vy+2P62。+26,式 92=…=9m=90: N 当跟随者不在领航者的感知范围内时, 中:Wy=2(。-月只.显然,是半正定函数。 ()=0:则4=-五7,,+0(g-g,),同 N jeN 戊=含78乐-或-y11 理采用李雅普诺夫稳定性定理方法可得q。= jENo qn+1=9n+2=…=qw,n<N. -qy(I+L(t))9≤0, 综上所述,所有个体渐进地取得和领航者相等 则领航者按事先确定的轨迹运行,且渐近地取得理 的速度矢量,且个体相互间保持稳定的间距;而领航 想的速度矢量,即po→p6,4o→q: 者按理想轨迹运行,P0→p6,9o→q6,故最终领航者 其次考虑跟随者,由于群体的平均距离和速度 引导群体按事先确定的轨迹运行,即p:→p→p。→ 分别A,=六云04=六宫Q则在相对坐标系 p6,9:→9→+90→90 2.2扰动性能分析 下,p:=p:-pe,9=q:-qe,p:=q,9:=4:-9e, 在实际应用中,由于存在多种于扰信息,往往会 N 造成通讯连接的失败、测量信息的不准确:致使群体 中的部分个体不能以较小的误差跟随群体运行,甚 当跟随者i在领航者的感知范围内时,h:(t)= 至跟踪失败. 1,且设有n个跟随者在领航者的感知范围内,则 结论1当群体受到外界干扰时,引入反馈机 4A+a,4)+ 制将减小由于扰动所引起的误差 证明假设将受于扰的个体列为群体中的最后 [90-c1(p:-po)-c2(9:-9a)], -1∑:= N m个个体,设速度矢量为q:=q:+e,E为扰动噪 9c-N 声,当无噪声干扰时跟踪误差为:e:=q:-qo,受噪声 干扰的群体的平均速度为 月-A+Aa-a)+ N一m jEN 豆=六公+月)=4+三 i, [90-c1(p:-p)-cz(9:-0)]}= i=N-m+l 则由于扰噪声引起的平均速度误差: 90+c(p0-pe)+c2(90-qe) 取p=[pp2…p]T,9=[2…]则控制律 6=9-4=六区 (4)可写成相对坐标系下的N个二阶系统与参考坐 设群体仍能保持群集运动,由定理可知q1= 标系下的一个二阶系统: 92=…=9w=qe,则受噪声干扰的群体的跟踪误差 p=4, 为e:=4:-90=g。-0=专+e:,则群体中所有个体 a.=-A+Aa-a)-6,-6a. 的跟踪误差均受到噪声的影响,且包括领航者周围 邻近的个体 p。=9q。, 领航者与邻近个体的平均跟踪误差和平均速度 9。=96-c1(p。-po)-c2(9。-9o).(5) 令=A,+分n,+2iaQ=A显 误差分别为:,=-(-AP,)-(9n- 然,Q1是半正定函数,对Q:求导得 品4)小当5变大时,跟随者速度变慢,跟随误差 0-名-a1-a1-1a1 增大,则ep、eg都将变大, 当平均速度误差专发生改变时,式(3)中的第2 -g(c,lw+L(t)9≤0. 项也跟着发生相应的变化.即当专变大时,跟随者速 取2={(po,P:)1Q1=0}中的最大不变集2,在集合 度变慢,跟踪误差变大,相应的式(3)的第2项变 大,反之跟随者速度变快,跟踪误差变小,相应的式 2中取Q=0,则V,=0.由LaSalle不变原理可知:系 (3)的第2项变小.故式(3)都将根据跟随者的跟踪 统的轨迹将收敛到区域2={(Po,P:)1Q=0}内的 误差的大小来调节领航者的速度,通过加快或减慢 最大不变集,由V=0可知:91=42=…=9m=9, 速度以适应群体的变化,从而减小了由于扰动所引 n<N.同理,由式(5)可推导出9。=9o;故91= 起的误差

·144 智能系统学报 第6卷 2.3容错性能分析 在实际应用中群体系统除了受扰动因素影响 外,还存在机械故障或网络故障(如执行器饱和或 -a5-7l 故障),使个体因硬件损坏而不能正常移动或因无 式中:H,=L,+B,H=L+B,B=diag(h(t),h2(t), 法与其他个体联系而掉队.因此群体必须具备容错 …,hw(t),L=[l]wxw表示所有跟随者组成的群 性才能成功地以群集运动的方式跟踪理想目标运 体对应的pacian矩阵,记@-[一 0 行.在无反馈机制的领航者-跟随者模式中,当领航 -ya令 者或者跟随者(该跟随者后面还有以它为参考点的 跟随者)出现故障时,将会使得群体中出现掉队现 且-yal、令e=P w= 0 c-@C. 象发生,群体可能无法按理想轨迹作群集运动.以 当群体对应的邻接图G为连通图时,对应的子 下将对具有反馈策略的群体进行容错性分析,结果 群S。的邻接图C也为连通图,故=L+B,H= 表明采用反馈策略的群体具有较强的容错性, f 在具有反馈机制的群体中,领航者与邻近个体 L+B均为正定矩阵,X= 01w+11 L-a-y 与= 之间通过无向边相连接,从而使得领航者和跟随者 IN T 具有相同的动态特性和相似的控制规律,即领航者 [-H-y 均为半负定矩阵, 可视为群体中的一部分.设领航者以及其邻近个体 当个体出现故障时,其速度可能为常数,从而使 形成的小群体S。内包含N+1个个体,S。={0,1, 得对应的控制输入为零.根据个体是否出现故障对 …,N},领航者(Po,9a)为小群体中的第0个个体, 各相关的状态变量以及X矩阵进行划分:e=[e (p6,6)为小群体的虚拟领航者.当取g=之(p.- en]T,其中ee,分别为对应出现故障的个体和正 P)2时,则小群体中的个体的控制律通式可写为 常个体的状态变量. 结论2当群体(包括领航者在内的所有个体) 4:=-c:(t)[(p:-p6)+y(q:-g6)]- 中的部分个体出现故障,且控制输人为零时,群体仍 A+Y(g-g),i=0.1,…, 能成功地跟随理想轨迹运行,形成群集运动,即 式中:co(t)=1,c(t)=0,i=1,2,…,No,即只有个 P:→卫→p0→p6, 体(po,qo)与虚拟领航者(p6,q6)相连接. 9:+9→90→96: 证明当领航者出现故障且,=0时,根据是 p:=p:-p6,9:=q:-q6,9=9 否出现故障对X矩阵进行划分: 上式可写成矩阵形式: (u)Bx (X12)1xwo 9-aa9 X= … L(X21)Mx1… (2)NoxNo 式中:a=+B,B=diag(co(t),…,cw,(t)为对角 由于=0,则 矩阵,2=[1,]w+)x%w表示小群体S,对应的 01x1 01xNo 0 Laplacia矩阵.记X-一A a令8-[1= -y (X21)Nox1 X2)Nx% re. 令 对于跟随者,令: 01x1 p:=p:-p0,9:=4:-90,P:=9, X L(X2)6x1 q:=4:-905g4 P:- X=5X, 式(4)等价为 则 a=A(a-)-Aaa-a》 r01x1 01xN6 I= h,(t)(cP:+c2q:) 写成矩阵形式:
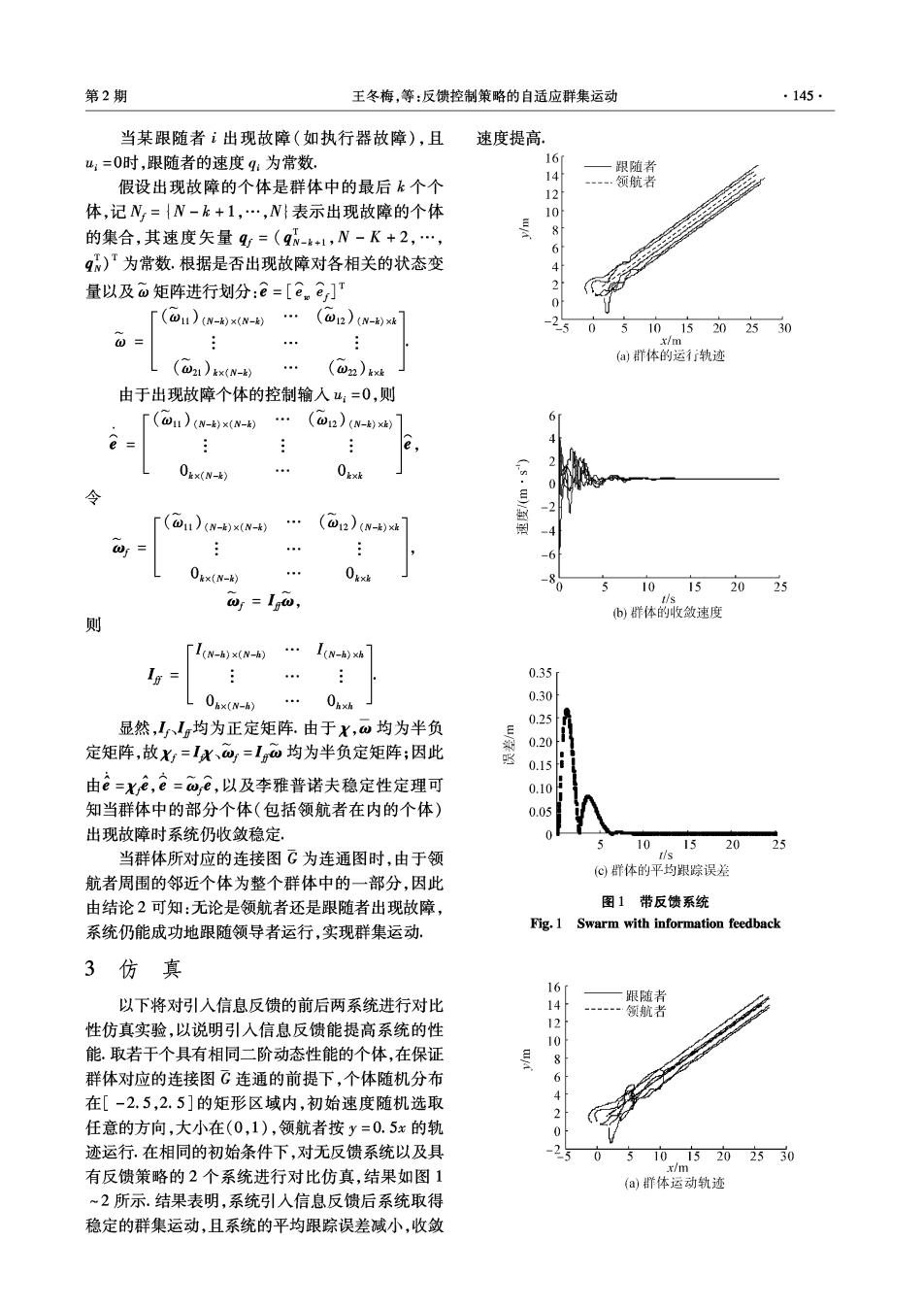
第2期 王冬梅,等:反馈控制策略的自适应群集运动 ·145 当某跟随者i出现故障(如执行器故障),且 速度提高, 4:=0时,跟随者的速度q:为常数. 16 跟随者 14 假设出现故障的个体是群体中的最后k个个 -…领航者 12 体,记N={N-k+1,…,W}表示出现故障的个体 10 的集合,其速度矢量q=(qN-k+1,N-K+2,…, 8 6 q)T为常数.根据是否出现故障对各相关的状态变 量以及0矩阵进行划分:e=[ene]T 3 厂(01i)(w-kx(N-·(®12)(w-X 25 0 51015202530 0 x/m (a)群体的运轨迹 (@2)kx(N-) (@)kxk 由于出现故障个体的控制输入山:=0,则 「(d1)w-xN-…(o2)- @ e ix(N-) Oixk 风 2 r(011)(w-)x(N-k) (012)(N-k)x =4 Ox(N-k) … Oxxck 5 10 1520 25 ws Igw, t/s b)群体的收敛速度 则 I(N-h)x(N-h) I(N-h)xh 0.35 Opx(N-) Oxk 0.30 显然,I、Ig均为正定矩阵.由于K,w均为半负 0.25 0.20 定矩阵,故X=IX、@=I0均为半负定矩阵;因此 驱 0.15 由e=Xe,e=0,e,以及李雅普诺夫稳定性定理可 0.10 知当群体中的部分个体(包括领航者在内的个体) 0.05 出现故障时系统仍收敛稳定, 1520 10 25 当群体所对应的连接图G为连通图时,由于领 (©群体的平均跟踪误差 航者周围的邻近个体为整个群体中的一部分,因此 由结论2可知:无论是领航者还是跟随者出现故障, 图1带反馈系统 系统仍能成功地跟随领导者运行,实现群集运动, Fig.1 Swarm with information feedback 3仿真 16 跟随者 以下将对引入信息反馈的前后两系统进行对比 14 领航者 性仿真实验,以说明引人信息反馈能提高系统的性 12 10 能。取若干个具有相同二阶动态性能的个体,在保证 群体对应的连接图C连通的前提下,个体随机分布 6 在[-2.5,2.5]的矩形区域内,初始速度随机选取 2 任意的方向,大小在(0,1),领航者按y=0.5x的轨 0 迹运行.在相同的初始条件下,对无反馈系统以及具 0 510.15202530 x/m 有反馈策略的2个系统进行对比仿真,结果如图1 (a)群体运动轨迹 ~2所示.结果表明,系统引入信息反馈后系统取得 稳定的群集运动,且系统的平均跟踪误差减小,收敛

.146. 智能系统学报 第6卷 [6]YU Hui,WANG Yongji.Control of stable flocking motion of multi-agent with a leader[J].Journal of Huazhong Uni- versity of Science and Technology:Nature Science Edition, 2005,33(8):56-58 [7 ]YU Hui,WANG Yongji.Stable flocking motion of mobile a- 多 gents following a leader infixed and switching networks[J]. International Joumal of Automation and Computing,2006,3 (1):8-16. 5 10 15 2025 [8]LEONARD N E,FIORELLI E.Virtual leaders,artificial tis b)群体的收敛速度 potentials and coordinated control of groups [C]//IEEE 1.4 Conference on Decision and Control.Orlando,USA,2001: 1.2 2968-2973. 1.0 [9]SABER R O.Flocking for multi-agent dynamic systems:Al- 0.8 gorithms and theory[J].IEEE Transactions on Automatic Control,2006,51(3):401420. 0.6 [10]WANG Long,SHI Hong,CHU Tiangguang.Flocking con- 0.4 trol of groups of mobile autonomous agents via local feed- 0.2 back[C]//IEEE Interational Symposium on Intelligent 10 15 20 Control.Limassol,Cyprus,2005:441446. t/s [11]SU Housheng,WANG Xiaofan,YANG Wen.Flocking in (©群体的平均跟踪误差 multi-agent systems with multiple virtual leaders[J].Asi- 图2无反馈系统 an Journal of Control,2008,10(2):238-245. Fig.2 Swarm without information feedback [12]SU Housheng,WANG Xiaofan,DONG Hairong,et al. Flocking with multiple virtual leaders based on position 4 结束语 measurements[C]//The 7th Asian Control Conference. Hong Kong,China,2009:1156-1161. 本文采用双向信息流策略将反馈机制引入到有 [13]BEARD R W,LAWTON J,HADAEGH F Y.A feedback 领航者的群集运动控制中,并分析了该策略的鲁棒 architecture for formation control[C]//American Control 性以及容错性.模型中领航者按事先确定的轨迹运 Conference.[S.L.],2000:40874091. 行,同时领航者需根据跟随者的状态信息自适应地 [14]WEI Ren,BEARD R W.Virtual structure based space- 调节自身的运行跟踪轨迹.研究分析表明该策略具 craft formation control with formation feedback[C]//AIAA 有容错性,且减小了系统的跟踪误差,提高了系统的 Guidance,Navigation,and Control Conference and Exhib- 鲁棒性,仿真结果证明了信息反馈策略能提高系统 it.Monterey,USA,2002:2002-4963. 的性能, [15]WANG Dongmei,FANG Huajing.Leader-following coordi- nation of multi-agent systems with information feedback 参考文献: [J].Journal of Systems Engineering and Electronics, 2009,20(4):16. [1]AMRITKAR R E,JALAN S.Self-organized and driven 作者简介: phase synchronization in coupled map networks[J].Physi- 王冬梅,女,1974年生,讲师,博士, caA,2003,321:220-225. 主要研究方向为网络化控制多智能体. [2]CZIROK A,VICSEK T.Collective behavior of interacting self-propelled particles[J].Physica A:Statistical Mechan- ics and its Applications,2000,281:17-29. [3]SABER R O.Flocking for multi-agent dynamic systems:al- gorithms and theory[J].IEEE Transactions on Automatic Control,2006,51(3):401420. [4]JADBABAIE A,LIN J,MORSE A S.Coordination of 方华京,男,1955年生,教授,博士 groups of mobile autonomous agents using nearest neighbor 生导师,主要研究方向为网络化控制系 rules[J].IEEE Transactions on Automatic Control,2003, 统、故障诊断、鲁棒与容错控制等. 48(6):988-1001. 5]LIU Y,PASSINO K M,POLYCARPOU M.Stability analy- sis of m-dimensional asynchronous swarms with a fixed com- munication topology[J].IEEE Transactions on Automatic Control,2003,48(1):76-95