
第7卷第2期 智能系统学报 Vol.7 No.2 2012年4月 CAAI Transactions on Intelligent Systems Apr.2012 D0I:10.3969/i.issn.1673-4785.201111016 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20120301.1652.001.html 自由角度显示系统下的运动向量算法 何雨兰,顾人舒,袁杰 (南京大学电子科学与工程学院,江苏南京210093) 摘要:为了解决三维运动矢量计算的问题,提出一种算法,这种算法是在静态三维重建的基础上用二维图片计算 刚体运动的线性方法,利用QR分解求解线性方程的最小均方误差解,迭代来消除离群值,来得到运动矢量.这种算 法不需要摄像机标定,实时性好,有利于视频的流畅显示,实验结果表明,此种算法具有一定的鲁棒性。 关键词:运动向量算法;运动估计:点匹配;线性方程组;QR分解 中图分类号:TP301.6文献标志码:A文章编号:16734785(2012)02011506 A 3-D motion vector algorithm in a free angle system HE Yulan,GU Renshu,YUAN Jie (School of Electronic Science and Engineering,Nanjing University,Nanjing 210093,China) Abstract:In order to solve a 3-D motion vector calculation,a new algorithm was proposed.This algorithm is a line- ar method that calculates the rigid-body movement from two-dimensional views based on the static 3-D reconstruc- tion.The QR decomposition was adopted to obtain the minimum mean square error of a linear equation set and an iterative process enables the method to eliminate outliers and thus obtain motion vector.This algorithm does not re- quire camera calibration,and it is real-time,which enables smooth video.The experimental results show the algo- rithm has good robustness. Keywords:motion vector algorithm;motion estimation;point correspondence;linear equation set;QR decomposition 在计算机视觉领域,从2幅或更多的图片序列法等方法0) 中估计三维运动参数刚体已被广泛研究了很长一段 然而,上述三维运动估计方法是从2幅(或2幅 时间,可以追踪到1970年左右,早期的研究证明,从 以上)图像没有任何先验知识的对象上来综合的, 平行投影模型来恢复运动,3个视角的图片是必要 一般来说,如何应用极几何约束是一个关键的问题 的;而从透视投影模型恢复运动,2个视角的图片就 至于基于点特征的方法,近期的工作集中在误差分 足够 析和控制1,12或集中在更好地估计基本矩阵315] 1989年,W.Huang等21详细论述了二维完全透 上,所有这一切都不可避免地运用了基础矩阵.最新 视投影的运动估计,提出了经典的8点算法,即利用 的相关工作161)使用无标定摄像机的2帧图像来 极几何(epipolar geometry)约束估计基本矩阵(矩阵 恢复结构和运动 E3)的特征点,然后从基本矩阵得到3-D运动参 1理论和算法 数.从那时起,为了克服它对噪声的敏感性,大量的 改进方法被提出,包括美国研究人员的规范化二维 1.1相机类型 数据的改进8点算法.除了基于特征点的方法外,研 仿射相机2-D坐标和3-D坐标服从以下规则: 究人员也提出了各种基于线特征的方法45、点线 特征结合的方法、光学流程6]和使用多帧、迭代算 收稿日期:2011-11-21.网络出版时间:20120301. 基金项目:江苏省自然科学基金资助项目(BK2010386). 通信作者:何雨兰,E-mail:hylzuo@yahoo.cn

·116. 智能系统学报 第7卷 [P1 P12P13 一对点都遵守这个等式,尽管旋转矩阵有9个元素, 式中:P= P21P22P23 ,P是决定从3-D空间到 它是一个正交矩阵,受6个独立的约束: 0 0 ∑=1,r=1,iw=1,2,3。 2-D平面线性映射的矩阵, 应当指出的是仿射相机是真实相机的近似,只 因而,矩阵中只有3个独立的元素.在各种不同 有当某一物体相对于自身的深度来说深度的变化可 的用3个元素表示R的方法中,以下2种方法是经 以忽略的时候,仿射相机是可以适用的, 常使用的,如图1所示. 1.2刚体运动模型 Roll 在3-D空间中,2个位置之间的刚体运动能够 (11,2n 被分解为旋转和平移.在3-D空间中,一个3×3的 Yaw 矩阵R能够描述刚体的旋转,一个3×1的矩阵T 能够描述翻译 Pitchy t ru 13 (a角轴表示3-D运动(b)Pitch-Rol-Yaw表示3-D运动 ,R= T21 T22 图1表示3-D运动的2种常用方法 T32 T33 Fig.1 Two expressions of 3-D motion 在图片中的任一特征点的3-D坐标为(X1,Y, 1)角轴表示法. Z),这些点在t1中的坐标为(1,Y1,Z1).则在0 (ru cos 0+(1-cos 0)ni, 与1之间的运动可以表示为 T2=(1-cos0)n1n2-(sin0)n3, X17 X r3 =(1-cos 0)nn3 (sin 0)n2, Y r21=(1-cos0)n12+(sin8)n3, t22=cos6+(1-co80)n2, L 1. rg=(1-cos0)n2n3-(8in0)n1, 运动矩阵则是: rat =(1-cos 0)ngm-(sin 0)n2, T12 T13 r32 =(1-cos 0)ngn2-(sin 0)n, M= T22 T23 t3=co80+(1-co80)n. T31 T32T33 3 L0 0 0 3-D矢量从开始的(0,0,0)到(n1,n2,n3)表示 值得注意的是,在一定的坐标系统下,刚体的任 刚旋转的坐标轴,它旋转的角度是0. 何一点都有相同的运动,即有相同的运动矩阵.任何 2)Pitch-Roll-Yaw表示法: C088,C086: -cos 0,sin 0. sin 0 sin 0 sin 0,cos 0.cos 0.sin 0. -sin 0.sin 0,sin 0.cos 0.cos 0.-sin 0.cos 0, cos 0.sin 0.cos 0.sin 0.sin 0. cos 0.sin 0,sin 0:sin 0.cos 0.cos 0.cos 0. 1.3求解运动问题 每一对点则给出2个等式: 1.3.1把运动估计的问题转化为解方程组 x=P14+P1t1+P12t2+P13t3+ X(pT+P12r21+P13r31)+ Y(Purn +Puar22 +Purs2)+ Z1(PirB+P12r3+P333), (1) y1=P24+P2141+P222+P233+ X X(paTu +para +pasrs)+ Y 则有如下已知等 Y1(P21T2+P2r22+P23r3)+ Z Z1(P2rB+P2r23+P3T33) 对小角度近似来说,如运动足够小,且假设运用

第2期 何雨兰,等:自由角度显示系统下的运动向量算法 ·117. Pitch-Roll-Yaw表示法,则旋转矩阵可以简化为 4 1 -30m28 厂1 -中3 中2 中 R= n01-n0= -0n01」 中3 1 YP8-ZPe ZPn -XPe XPe -YPn Pu PePe L-2中 1 YiPa-ZPz ZiPa -XiPs XiPe -YiPa Pa Pa Ps 式中:(n0)2+(n20)2+(n0)2=fΦ+φ2+=f., 重写等式组(1): .t3 -Pu-XiPa -YiPn ZiPB]= 多个点对点的等式组如下: yi-pa X Pa YiPz -ZPa 「x-P4-XP1-YPe-ZPs7 YPB -ZIPR ZiPu-X Pn3 XPn -YiPu PuPuPu φ1 YiPas-ZiPn ZiPa X Pas X Pn -YiPa PaPa Pas 中2 y1-P24-X1P21-YiP22-Z1P23 中 YPy-ZPR ZPu XP XPR2 -YPu Pu Pr t -Pu-XaPu YaP12 -ZnP13 P13 yh Px X.P2 YaPz2 -ZP23 LYP2 -ZPn ZaPa X.P23 X Pn YnPa Pa Pn P2s- t n=1,2,…. 上述等式的右侧第1个矩阵写作A,它的秩不 对于得到的矩阵(2),右边3列作为一个子矩 超过5.这是单摄像机的限制,因为摄像机不能给出 阵P,它的秩最多为2,因为只有2行非零行;左边3 光轴沿的深度信息.观察矩阵A.发现右边3列的奇 列作为一个子矩阵Y,它的秩最多为3,所以矩阵 数行数相同,偶数行也如此.对矩阵A进行初等变 (2)的秩最多为5,M=[YP],rank(Y)≤3, 换,利用首行消除右边3列的2-1行,用第2行来消 rank(P)≤2,rank(M)≤5.初等变换不改变矩阵的 除这些行的2i行(i=2,3,…,n): 秩,所以矩阵(2)的秩最高为5.因而知道刚体的运 YPe -ZPe ZPu -XPe XPe -YPa Pu PePe 动估计至少需要2台摄像机.第2台摄像机的投影 YPs-ZPz ZPa-XPs XiPe-YiPa Pa Pe Ps :00 矩阵为 0 pPu ppu2 pp3 PP14 000 PP PP2 PP23 Y.Ps -ZPe ZPu -XPe X.Pe -Y.Pu 000 0 0 YPs -ZPz Z.Pa -XPa XPa -Y.Pa 000 已知, (2) -P1 -XiPu YiPn2 Z PI3 y1-P24-XP21-Y1P22-Z1P23 h-PP14 X PPu Y PPR -Z P3 -ya -ppa X,PPa YaPpz -Z.Pa YP13-Z1P12 ZiPu -XiPB XiPn2-YiPu Pu P12 P13 YPzs-ZPa 中2 ZiPa -XiP2s XiPn-YiPz P21 P22 P23 ,n=1,2,… YaPPis ZaPPu ZaPpu -Xappis X.PPn -YaPPu h ppu PPu PPi3 LY,PPa -Z.PPz ZPpa -XPP2s XPPz -YPPa PPa PP22 PP23

118 智能系统学报 第7卷 左边的矩阵则表示为b,右边的矩阵则表示为 50 1 Ax.因此,运动估计问题转化为求解方程组b=Ax 使用从摄像机1中得到的m个点对和从摄像 450 550 机2中得到的k个点对,条件是n=m+k(m,n≥ 02468101214× 10 像素 1).理论上,从2台摄像机上得到的3个点对足够解 (a)来自摄像机1的图片(左)和图片1(右)的匹配点 方程组.当n≥3时,需要解方程组来导出结果.在利 用图片6和t1进行图像匹配的3-D重建后,可以获 150 6250 得大量的特征点对.为了利用所有的信息,首先使用 350 450 所有的点进行运动估计,并且为了提高算法的鲁棒 550 022 68101214×10° 性,利用运动矩阵的初始解来进行二次投影,在图片 像素 1中,把结果与真实的2-D坐标进行比较,消除大于 (b)来自摄像机2的图片(左)和图片5(右)的匹配点 阈值10的异常值(实验结果表明误差一般小于5, 图2摄像机1、2的图片。和图片1的匹配点 Fig.2 Matched point pairs in image to and t from 如果错误大于10,它可能是一个异常值).异常值的 cameras 1 and 2 出现可能是误匹配的结果。 1.3.2通用算法 如果没有小角度近似,那么可以写出如下方程组: X一P4 Xp XPe XiPs YiPu YiPe YiPe ZPu ZPeZPe Pu PePe y-Pa Xp Xpz Xipa Yipa Ypz Yipa Zipa Zopz Zapa Pa P2 Pa (3) 一P4 x,PuX理eX理BY,uY,nY吧s ZaPPu ZaPe ZaPPe PPu厘ePB -PPw xPP2 X,PPz X.PPz YPPa YPPz YPPa Z.PPa Z Pz ZaPPa PPu PPz PPs- 使用从摄像机1中得到的m个点对和从摄像 +川b2I2 机2中得到的k个点对,条件是n=m+k(m,n≥ 注意到‖b2‖是常数,所以原问题 1).求解方程组的方法(3)与近似算法相同.对于式 min I A-bI2转化为min‖Rr-b1‖2,即Rxr- (3)来说, b1=0.故有 x= x=R-b. (4) [ru2r2T1T2TBr3Tt吃]. 至此,x向量已经解出.对于式(2)的近似算法,x= 对于通用算法,为了保证已满秩,至少需要4+ [中,中,中t12]';对于式(3)的非近似算 4=8对特征点. 法,x=[r1T21T31T12T2T32T3T3T33 1.3.3求解线性方程组的最小均方误差解 6166]. 采用QR(正规正交矩阵一上三角形矩阵)分解 法,解法如下: 2实验验证 由于误差的存在,Ax=b+e,问题是求解x使 利用Matlab对提出的算法进行验证,以下是算 范数‖ε‖2最小 法的流程, 可以找到0使得04=[的 其中Q为正交矩 1)3-D重建; 2)匹配图片t和t1,获得t1中特征点对的二维 阵,R为非奇异上三角阵, 坐标; Is2=Ax-b2=2(Ax-b)12= 3)双目视觉:3-D重建和2台摄像机的图片匹配; 10ax-Qb1i=1[6]-Q1, 4)初始化:输人摄像机1的m对点和摄像机2 的k对点; 5)运动估计转化为解方程组,每个点对给出2 个方程; 于]是列向量,故IAr-b3=1c-b1 6)解方程组b=Ax(运用QR分解); 7)用导出的M投影,把2-D结果与真实的2-D
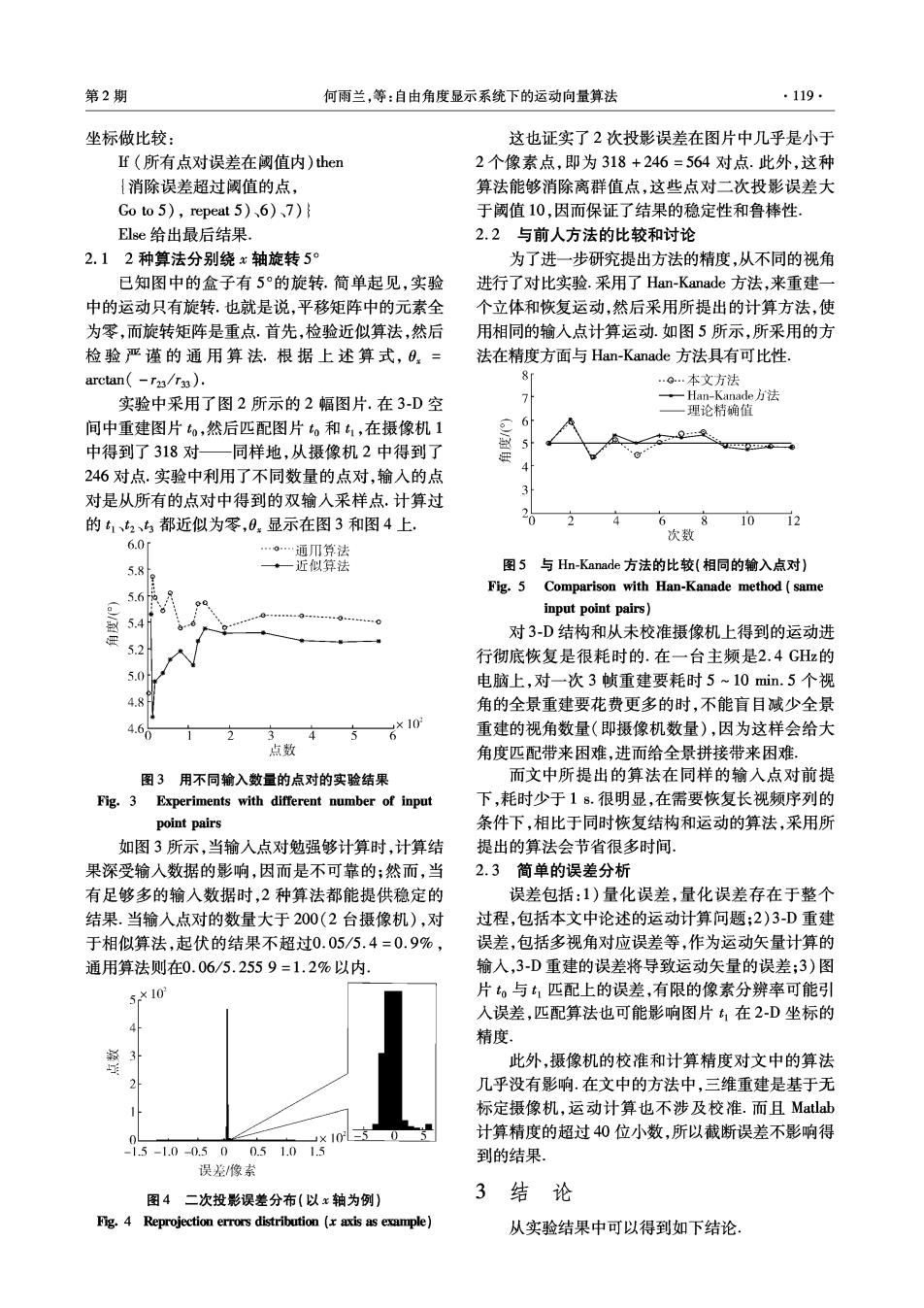
第2期 何雨兰,等:自由角度显示系统下的运动向量算法 ·119 坐标做比较: 这也证实了2次投影误差在图片中几乎是小于 f(所有点对误差在阈值内)then 2个像素点,即为318+246=564对点.此外,这种 {消除误差超过阂值的点, 算法能够消除离群值点,这些点对二次投影误差大 Goto5),repeat5)、6)、7)i 于阈值10,因而保证了结果的稳定性和鲁棒性, Else给出最后结果. 2.2与前人方法的比较和讨论 2.12种算法分别绕x轴旋转5° 为了进一步研究提出方法的精度,从不同的视角 已知图中的盒子有5°的旋转.简单起见,实验 进行了对比实验.采用了Han-Kanade方法,来重建一 中的运动只有旋转,也就是说,平移矩阵中的元素全 个立体和恢复运动,然后采用所提出的计算方法,使 为零,而旋转矩阵是重点.首先,检验近似算法,然后 用相同的输入点计算运动.如图5所示,所采用的方 检验严谨的通用算法.根据上述算式,日,= 法在精度方面与Han-Kanade方法具有可比性, arctan(-r2a/r3). .。…本文方法 实验中采用了图2所示的2幅图片.在3-D空 一Han-Kanade方法 -理论精确值 间中重建图片,然后匹配图片和t1,在摄像机1 中得到了318对一同样地,从摄像机2中得到了 246对点.实验中利用了不同数量的点对,输入的点 对是从所有的点对中得到的双输入采样点.计算过 2 的1、都近似为零,0显示在图3和图4上. 6 81012 次数 6.0 …o…通兀法 5.8 *一近似算法 图5与Hn-Kanade方法的比较(相同的输入点对)】 9 Fig.5 Comparison with Han-Kanade method(same 5.6 input point pairs)】 54 对3D结构和从未校准摄像机上得到的运动进 八3 行彻底恢复是很耗时的.在一台主频是2.4GHz的 电脑上,对一次3帧重建要耗时5~10min.5个视 4.8 角的全景重建要花费更多的时,不能盲目诚少全景 460 3 4 6*10 重建的视角数量(即摄像机数量),因为这样会给大 点数 角度匹配带来困难,进而给全景拼接带来困难。 图3用不同输入数量的点对的实骏验结果 而文中所提出的算法在同样的输入点对前提 Fig.3 Experiments with different number of input 下,耗时少于18.很明显,在需要恢复长视频序列的 point pairs 条件下,相比于同时恢复结构和运动的算法,采用所 如图3所示,当输入点对勉强够计算时,计算结 提出的算法会节省很多时间 果深受输入数据的影响,因而是不可靠的:然而,当 2.3简单的误差分析 有足够多的输入数据时,2种算法都能提供稳定的 误差包括:1)量化误差,量化误差存在于整个 结果.当输入点对的数量大于200(2台摄像机),对 过程,包括本文中论述的运动计算问题;2)3-D重建 于相似算法,起伏的结果不超过0.05/5.4=0.9%, 误差,包括多视角对应误差等,作为运动矢量计算的 通用算法则在0.06/5.2559=1.2%以内 输入,3-D重建的误差将导致运动矢量的误差:3)图 10 片。与t,匹配上的误差,有限的像素分辨率可能引 入误差,匹配算法也可能影响图片t1在2-D坐标的 精度 此外,摄像机的校准和计算精度对文中的算法 17 几乎没有影响.在文中的方法中,三维重建是基于无 标定摄像机,运动计算也不涉及校准.而且Matlab ux 10 计算精度的超过40位小数,所以截断误差不影响得 -1.5-1.0-0.500.51.01.5 到的结果. 误差/像茶 图4二次投影误差分布(以x轴为例) 3结论 Fig.4 Reprojection errors distribution (x axis as example) 从实验结果中可以得到如下结论

·120 智能系统学报 第7卷 1)提出算法的正确性和有效性得到了验证.对 [11]SAND P,TELLER S.Particle video:long-range motion 于相似算法,需要至少3个点对来进行运动估计,但 estimation using point trajectories[J].International Jour- 是算法的结果很大程度上依赖所取得的3个点对, nal of Computer Vision,2008,80(1):72-91 因而是很敏感、不稳定的。 [12]MATEI B,MEER P.A general method for errors-in-varia- bles problems in computer vision C]//Proc IEEE Conf 2)当有足够多的数据时,所提出的算法是稳定 Computer Vision and Pattern Recognition.Hilton Head, 的,且具有鲁棒性,它可以消除离群值.最后,提出的 USA,2000:18-25. 算法是很简洁的.时间的消耗取决于点对的数量,通 [13]FIROOZFAM P,NEGAHDARIPOUR S.Theoretical accu- 用的算法只需要0.08,近似算法需要大约0.1s. racy analysis of nocular vision systems for scene reconstruc- 参考文献: tion,motion estimation,and positioning problems in com- puter vision[C]//Proc 2nd Int Symposium on 3D Data [1]PAPADIMITRIOU T,STRINTZIS M G,ROUMELIOTIS Processing,Visualization,and Transmission.Washington, M.Robust estimation of rigid body 3-D motion parameters DC,USA,2004:88-895. based on point correspondences[J].IEEE Trans on Cir- [14]SHEIKH Y,HAKEEM A,SHAH M.On the direct esti- cuits and Systems for Video Technology,2000,10(4): mation of the fundamental matrix[C]//Proceedings of the 541-549. IEEE Conference on Computer Vision and Pattem Recogni- [2]WENG J,HUANG T S,AHUJA N.Motion and structure tion.Minnesota,USA,2007:1-7. from two perspective views:algorithms,error analysis,and [15]CHEN P.Why not use the Levenberg-Marquardt method error estimation[J].IEEE Trans on Pattern Analysis and for fundamental matrix estimation[J].IET Computer Vi- Machine Intelligence,1989,11(5):451-476. sion,2010,4(4):286-294. [3]HARTLEY R.In defense of the 8-point algorithm [C]/ [16]WU HH P,CHANG S H.Fundamental matrix of planar IEEE International Conference on Computer Vision.Cam catadioptric stereo systems[J].IET Computer Vision, bridge,USA,1995:1064-1070. 2010,4(2):85-104. [4]EBRAHIMNEZHAD H,ROBUST H G.Motion from space [17]SZELISKI R.Computer vision:algorithms and applications curves and 3D reconstruction from multiviews using perpen- [M].Berlin:Springer-Verlag,2010:343-374. dicular double stereo rigs[J].Image and Vision Compu- 作者简介: ting,2008,26(10):1397-1420. 何雨兰,女,1988年生,硕士研究 [5]MONTIEL J MM,TARDOHS J D,MONTANO L.Struc- 生,主要研究方向为3-D重建算法。 ture and motion from straight line segments [J].Pattem Rec0 gnition,2000,33(8):1295-1307. [6]STEINBACH E G,EISERT P,GIROD B.Model-based 3-D shape and motion estimation using sliding textures[C] Proc Vision Modeling and Visualization Conference.Berlin, Germany,2001:375-382. 顾人舒,女,1989年生,硕士研究 [7]NEUMANN J,FERMULLER C,ALOIMONOS Y.Polydioptric 生,主要研究方向为3-D重建算法, camera design and 3D motion estimation[C]//Proc IEEE Conf Computer Vision and Pattern Recognition.Madison,USA, 2003:294-301. [8]ROACH J W,AGGARWAL J K.Determining the move- ment of objects from a sequence of images[J].IEEE Trans on Pattern Anal and Machine Intell,1980,7(4):554- 袁杰,男,1975年生,副教授,主要 562. 研究方向为3D重建算法、嵌入式系 [9]OLIENSISA J.Multi-frame structure from motion algorithm 统 under perspective projection[J].International Joumal of Computer Vision,1999,34(2):163-192. [10]付永庆,宋宝森,吴建芳.边缘分类SFT算法[J].哈尔 滨工程大学学报,2010,31(5):163171. FU Yongqing,SONG Baosen,WU Jianfang.Edge classifi- cation of the SIFT alogorithm[J].Journal of Harbin Engi- neering University,2010,31(5):163-171