
第6卷第3期 智能系统学报 Vol.6 No.3 2011年6月 CAAI Transactions on Intelligent Systems Jun.2011 doi:10.3969/i.issn.1673-4785.2011.03.009 采用一致性算法与虚拟结构的 多自主水下航行器编队控制 袁健,唐功友 (中国海洋大学信息科学与工程学院,山东青岛266100) 摘要:采用一致性算法与虚拟结构法研究了多自主水下航行器(AUV)小尺度编队控制问题.首先针对各自主水下 航行器拥有不同虚拟领航者信息(参考信息)的情况,通过对各AUⅣ拥有的不一致参考信息进行一致性协商而达到 状态一致.其次,基于虚拟结构思想采用坐标变换将各AUV相对于虚拟领航者的相对位置转换为各自的期望位置, 并设计了一种有限时间跟踪控制律以确保各AUV能在有限时间内跟踪上其期望轨迹,从而实现了多AUV的小尺度 有限时间编队控制.最后仿真实验验证了控制策略的有效性, 关键词:自主水下航行器;编队控制;一致性算法;虚拟领航者 中图分类号:TP24文献标识码:A文章编号:16734785(2011)03024806 Formation control of autonomous underwater vehicles with consensus algorithms and virtual structure YUAN Jian,TANG Gongyou College of Information Science and Engineering,Ocean University of China,Qingdao 266100,China) Abstract:The small-scale formation control of autonomous underwater vehicles AUVs)was investigated with con- sensus algorithms and virtual structure.Firstly,considering the inconsistant virtual-leader information (reference information)for each AUV,a consensus algorithm was adopted to negothiate the inconsistant reference information for each AUV,helping them reach a consistant state.Secondly,the relative positions to the virtual leader were transformed into their desired positions with coordinate transformation based on virtual structure,and a control law was proposed to make the AUVs track the desired trajectories in finite time.The small-scale formation control for AUVs in finite-time was carried out.Finally,Experimental results were provided to demonstrate the effectiveness of the proposed methods. Keywords:autonomous underwater vehicle;formation control;consensus algorithms;virtual leader 多自主式水下航行器的协同作业可以显著提高 位置和姿态的一致性问题 AUV在海洋采样、成像、监视和通信等众多应用方 本文针对在不一致参考信息情形下多AUVs的 面的能力.目前关于多AUVs编队控制的研究结果 通信时延和数据掉包问题,研究了多AUVs基于 主要借鉴了陆地多机器人(或多智能体)协同控制致性算法和虚拟结构的编队控制问题.首先,采用一 策略刃.与陆地多机器人编队控制相比,在信号传 致性算法对各AUV拥有的不同虚拟领航者信息进 输方面AUVs所采用的通讯介质为水声,随着通讯 行处理,通过对这些不一致参考信息进行一致性协 距离的增加通信质量显著下降,主要表现在信号的 商而达到状态一致;针对数据掉包问题,将多AUVs 延迟、衰减和失真13).多AUV编队控制要求系统最 通信网络建模转换为切换拓扑的一致性问题,研究 终能够实现预先定义的编队形状,可将多AUV系统 切换拓扑情形下的一致性跟踪问题.其次,将各 建模为多智能体系统,采用一致性算法[84]研究其 AUV相对于虚拟领航者的相对位置转换为各AUV 收稿日期:2010-05-26. 的期望位置,并设计了一种有限时间跟踪控制律以 基金项目:国家自然科学基金资助项目(61074092) 确保各AUV能在有限时间内跟踪上期望轨迹.最后 通信作者:袁健.E-mail:jyuanjian801209@163.com. 以3个AUV构成的通信网络为例,仿真验证了控制

第3期 袁健,等:采用一致性算法与虚拟结构的多自主水下航行器编队控制 ·249· 策略的有效性, 合;xo(t)满足(t)=f(x(tw));bm>0. 1问题描述 网络环境下的数据掉包会导致系统收敛速度下 降,数据掉包示意图如图1所示,图中+代表 在多AUV系统中,个体AUV动态描述如下: AUV(i)的第k+n个更新时刻.只要通信信号丢失 x:(t)=u:(tk),i∈P. (1) 则视该链路失效(数据掉包),即此时通信拓扑发生 式中::(k)=[x(k)y()0()]T∈R3,其中 变化,可以将其建模转换为切换拓扑的一致性问题 x(tw)y(t)、0(t)分别表示时刻各个AUV所 来研究 拥有的虚拟领航者的位置和驶向角;:(k)为相应 AUVU) 维数向量,表示,时刻控制输人;P={1,2,…,p}表 示所有AUV的集合 对于系统(1),可以取控制输入为 u:()=∑ag(x,()-x(). AUV() 防e啡 式中:W表示,时刻个体i的邻居个体集;ag>0为 1…t++1++2+n+++4++ …数据掉包—未掠包 有向图G=(V,E)的邻接矩阵A的邻接权重。 式(1)的紧凑形式为 图1AUV()时延和数据掉包 (t)=-Lx(t). (2) Fig.1 Time-delay and data-dropout of AUV(j) 式中:x()=[x()x2()…x,()];L为有向 2.2多AUV系统编队控制算法 建立2个平面直角坐标系,分别为X-0-Y坐标 图的pd矩阵并且L=D-A,D=,名A,为常 系和虚拟领航者本体坐标系v-o-以.定义(X*,Xr) 数矩阵 为AUV(i)的实际位置,(X,X)为AUV(i)的期望 给出下面的定义和引理。 位置.则可以将AUV()在-o-v坐标系下的坐标 定义1如果对于每一个AU节点对(:,), 转换为X-0-Y坐标系下的坐标,其表示为 :,四∈V(V为边集),当≥t。时都有‖x:(4)- 七,(t)‖=0,则称AUV构成的网络G=(V,E)在 t≥t。时处于一致性状态 式中:[x:y:]T表示AUV()所具有的虚拟领航者的 引理1]网络拓扑结构固定不变时,当且仅 位置;[矿力表示AUV()相对于编队几何中心的 当网络图包含一个生成树,式(2)所描述的系统渐 期望偏离量,如图2所示。 近达到一致. ,X() 2 基于一致性的多AUV系统编队控 制算法 x(2 X( x( 2.1具有动态参考信息的一致性算法 及因 X( 对于在较长时间内,各AUV获取的参考信息是 X(t 时变的,故需要研究具有动态参考信息的一致性问 题.各AUV所拥有的参考信息的由于信号失真,可 !期望位置 实际位置 F 能导致略有偏差,则对虚拟领航者进行协商的一致 性算法为: 图2基于一致性的编队控制 Fig.2 Consensus-based formation control ()=∑ag(()-(4),ief月 因此AUV()平面内运动学方程为 ()=∑ag(x()-x()+ 「cosg:07 sin:0 ba(xo(t)-x;(t)),iL. (3) 1 式中:∫为所有跟随者的集合;1为所有领航者的集 式中:P:=[XX:]T表示AUV(i)的运动状态;

250. 智能系统学报 第6卷 9:=[:ω:]T表示控制输入,、ω:分别为AUV(i)的 下设计步骤进行. 线速度和角速度;:=arctan(Xy/Xa)为驶向角. 对系统(4)的状态0进行一阶系统有限时间控 轨迹跟踪问题就是要找到、ω:的控制律使 制设计,选择ω:的控制律为 AUV(i)跟踪参考轨迹[XXg]和参考速度输人入 0:=+k10+k28gm(0a). (6) 、w,如图3所示。 式中:k1,k2>0,则有0。.=-k0.-k2g(0).因 此由引理2知,系统(4)在有限时间t。内到达0= 0,其中t。=-ln(2/(k2-k0ng(0))/k1,且系 统(4)在有限时间t。内到达o:=o. 对系统(4)在t>t。时,只需考虑另2个状态的 图3轨迹跟踪控制 控制设计.由于变结构控制的存在,导致0在平衡 Fig.3 Trajectory-tracking control 在机器人本体坐标系下的位姿误差定义为 点附件有小的抖振,即0:∈{10=1,-|0msI},故此 时原系统可写为: cos sin x=wiyai -vi+vcos 0n, P= -8in:c08: 0 ya=-+vsin (7) -0a 0 0 由于0:为在平衡态附近变化的小量,(t)连续有 X6-X 界,故sin80,所以式(7)可以化简为: (4) %=wiyai-vi+vcos Oai, g- yi=-ωixar 式中:T。为从惯性坐标系到机器人本体坐标系的转 因此可将状态0首先调整为0,使得状态y.的变化 换矩阵.对式(4)求时间导数,误差的动力学方程可 完全由v:来控制. 以写为5: 下面对状态(x。,y。)组成的线性系统进行设计. £a=ωy-:+ico80, 引理3[6双积分线性系统1=,:2=山可 yd=-ωxa+vsin日, 被控制器u=-专3g知(x1)|x11-专4g(x2)1x21 0。=-w (5) 在有限时间内镇定,其中00,0>B1>1,B2=2B/(1+B),得到子 框图如图3所示,其中参考轨迹p:是参考输入q 系统闭环形式为: 通过参考系统得到的系统输出,NC为非线性控制 器,1为受控AUV系统(4),Σ:为参考系统的运动 %=-kasgn(y)I ya l-kasgn() (9) 学方程: Yai =-Wixi 由引理3知xay在有限时间到达0. cos 0i 0 由此得到如下定理 sin 0' 0 定理1若(t)∈[0,o)连续有界,且w= 0 1 C≠0,则控制律(6)和(8)使得系统(4)状态在有限 3 轨迹跟踪控制器设计 时间到达零,且满足闭环系统是有限时间稳定的, 系统(4)在有限时间内能跟踪上参考轨迹 引理2线性系统云=u可被控制器4=专1x+ 证明由上述控制律设计过程可知系统(4)在 52g(x)在有限时间内镇定,其中51,2t。时子系统(7)一致渐近 其中t,=-n(52/(52-5gm(x))/传 稳定 考虑到移动机器人运动学模型特性,将有限时 1)状态x和y在t≤t。内的有界性. 间控制技术应用于移动机器人的跟踪控制,可按如 将控制律(6)和(8)代入系统(4),得到如下闭

第3期 袁健,等:采用一致性算法与虚拟结构的多自主水下航行器编队控制 ·251 环系统: 件,且切换拓扑的并集为平衡图,所以最终可以达到 %ai =ki0ayai +k28gn(0i)yai- 参考状态的一致性.一致性协商的仿真结果如图5 3gn(ya)lyaI-k4sgm(xa)1xa, ~10所示.从图中可以看出0~48内,3个AUV状 yai =-[o:+k10ni +kasgn(0)]x+vsin 0, 态达到了一致,形成了预定的编队形状.4~108内, 0n=-k0n-k28gm(0n). 由于AUV(2)和AUV(3)无法获取领航者信息,而 取关于状态xa和ya的Lyapunov函数: AUV(1)可以获取领航者信息;所以AUV(2)和 (a》=+. AUV(3)与AUV(1)相比,更加偏离领航者状态,导 致本来已经形成的编队形状遭到破坏.108以后,随 求导数得 着时间的推移,所有AUV最终达到了一致的状态, Vi(xi,ya)=-kasgn(ya)xal yal- 即形成了预定的编队形状 kasgn()x-wyi-viyasin Oa 2.5 AUV(1) +AUV(2) (10) 2.0 由于状态0在有限时间到达0。.=0,状态0在任意 金。=0唐e和Ee0知口AUV{3) g1.5 时间均为有界,并且假设和w有界,则可验证对 于式(10),一定存在合适的7>0,{>0,使得对任意 1.0 o1-4S ‖xaya‖>n,有(xa,ya)≤V(xi,ya).因此,在 0.5 ≤t。有限时间区间内状态x。和y.是有界的. 0 2)状态x和y.在t>t。的有限时间收敛性 0.4 0.81.21.62.0 x/m 当t=t。时,0为在0。=0附近的小量,故当t> 图50~4s时间段虚拟领航者轨迹 t。时由于变结构控制的存在,0∈{|0mr|, Fig.5 Trajectories of virtual leaders from 0s to4s -I0rI}并在10=I和-10ma|来回切换,此时子系 统可近似为式(9),由引理4知xy在有限时间内 1.8 稳定 AUV(1) 1.6 .AUV(2) 4数值仿真 AUV3ooa000000000 1.4 设某海域有由3个AUV组成的AUV通信网 1.2 络,其通信网络拓扑如图4所示.仿真步长△T= 0.018,仿真时间T=158. 1.0 =10 0.80.91.0 1.2 1.41.61.8 x/m 图64~10s时间段虚拟领航者轨迹 h Fig.6 Trajectories of virtual leaders from 4 s to 10 s 图4切换拓扑 1.5 Fig.4 Switched topologies 图4(a)所示为全通平衡网络,并且所有AUV .. 均可获取虚拟领航者的参考信息.图4(b)中 AUV(2)和AUV(3)的通信链路失效,并且仅有 110s AUV(1)可获取虚拟领航者的参考信息.图4(c)中 0.9 AUV(1)和AUV(2)的通信链路失效,AUV(1)和 S88 m产DA ·AUV(2) AUV(3)可获取虚拟领航者的参考信息. 口AUV(3) 设虚拟领航者的参考信息时变特性描述为 0.0.60.7 0.91.11.3 1.5 x/m xo(t)=[1+cos2tk1+sin2tk1+2t].设在T在 图710~15s时间段虚拟领航者轨迹 15s时间内由于数据掉包而导致通信拓扑在图4 Fig.7 Trajectories of virtual leaders from 10 s to 15 s (a)~(c)顺序切换,切换时刻为t=4,10s时,切换 顺序为(a)→(b)→(c).由于达到一致性的必要条
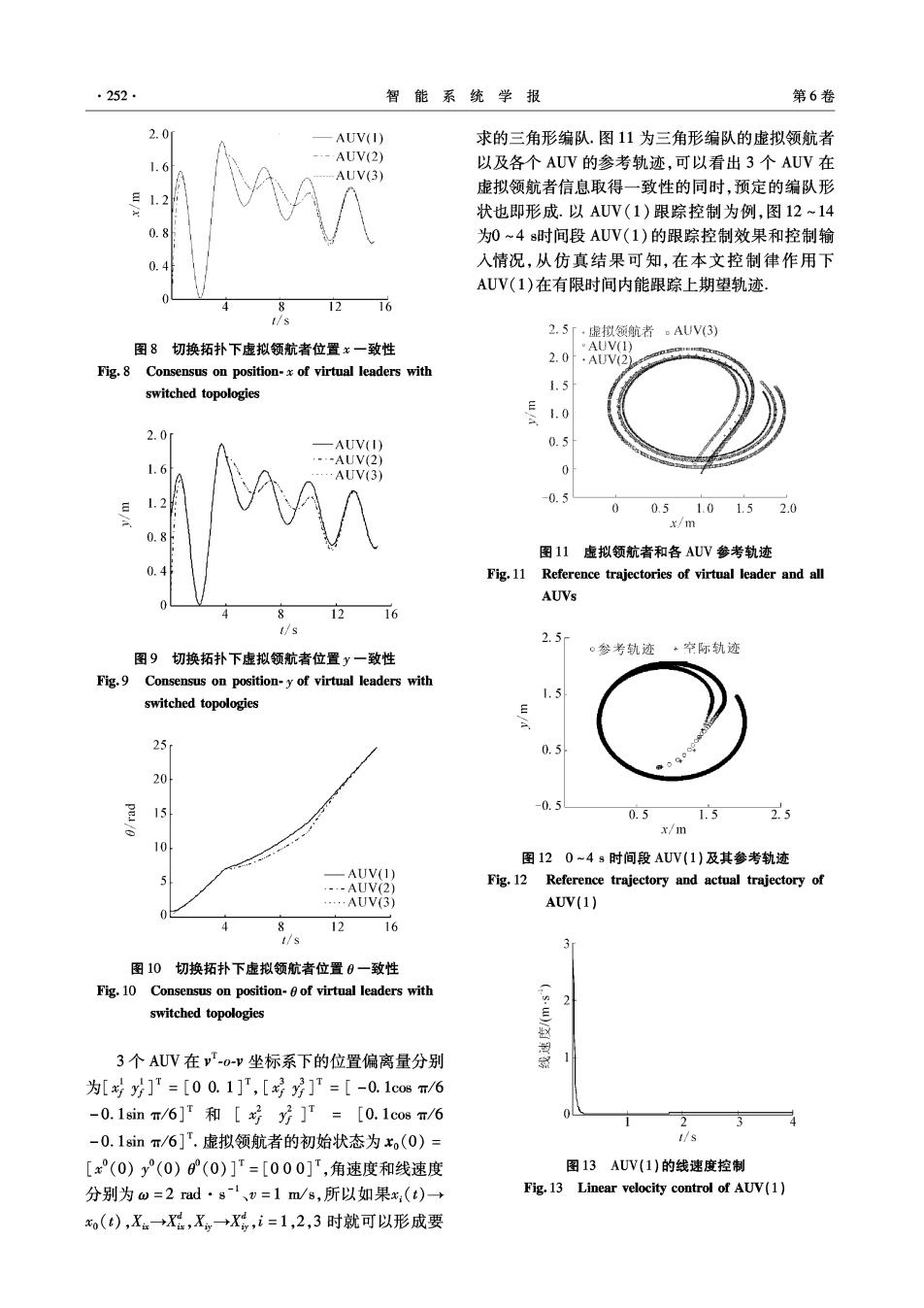
·252. 智能系统学报 第6卷 2.0 AUV(I) 求的三角形编队.图11为三角形编队的虚拟领航者 AUV(2) 1.6 以及各个AUV的参考轨迹,可以看出3个AUV在 AUV(3) 虚拟领航者信息取得一致性的同时,预定的编队形 状也即形成.以AUV(1)跟踪控制为例,图12~14 0.8 为0~4s时间段AUV(1)的跟踪控制效果和控制输 0.4 入情况,从仿真结果可知,在本文控制律作用下 AUV(1)在有限时间内能跟踪上期望轨迹. 8 12 16 t/s 2.5「·虚拟领航者。AUV(3) 图8切换拓扑下虚拟领航者位置x一致性 °AUV(1) 2.0 .AUV(2) Fig.8 Consensus on position-x of virtual leaders with switched topologies 1.5 1.0 2.0 AUV(I) 0.5 --AUV(2) 1.6 AUV(3) 0 1.2 -0.5 0 0.51.01.52.0 x/m 0.8 图11虚拟领航者和各AUV参考轨迹 Fig.11 Reference trajectories of virtual leader and all AUVs 12 16 t/s 2.5 。参考轨迹·空际轨迹 图9切换拓扑下虚拟领航者位置y一致性 Fig.9 Consensus on position-y of virtual leaders with 1.5 switched topologies 25 0.5 30 15 0.5 0.5 1.5 2.5 x/m 10 图120~4s时间段AUV(1)及其参考轨迹 -AUV(1) 5 .--AUV(2) Fig.12 Reference trajectory and actual trajectory of …AUV(3) AUV(1) 8 12 16 t/s 3 图10切换拓扑下虚拟领航者位置0一致性 Fig.10 Consensus on position-0 of virtual leaders with 2 switched topologies 3个AUV在v-o-v坐标系下的位置偏离量分别 为[对]=[00.1],[g]=[-0.1co8m/6 -0.1sinm/6]F和[号号T=[0.1co8m/6 2 3 4 -0.1sinπ/6].虚拟领航者的初始状态为x(0)= t/s [x°(0)y°(0)0(0)]T=[000]',角速度和线速度 图13AUV(1)的线速度控制 分别为w=2rad·8l、v=1m/s,所以如果:(t)→ Fig.13 Linear velocity control of AUV(1) x(t),X.→X,X,→X,i=1,2,3时就可以形成要

第3期 袁健,等:采用一致性算法与虚拟结构的多自主水下航行器编队控制 ·253· 50 homogeneous swarms of autonomous underwater vehicles [J].Autonomous Robots,2007,22(1)37-53 [8]DEGROOT M.Reaching a consensus[J].Journal of Amer- 3 ican Statistical Association,1974,69(345):118-121. [9]BORKAR V,VARAIYA P.Asymptotic agreement in dis- tributed estimation[J].IEEE Transactions on Automatic Control,1982,27(3):650-655. [10]TSITSIKLIS J,ATHANS M.Convergence and asymptotic 2 agreement in distributed decision problems[J].IEEE t/s Transactions on Automatic Control,1984,29(1):42-50. 图14AUV(1)的角速度控制 [11]VICSEK T,CZIROK A,JACOB E,et al.Novel type of Fig.14 Angular velocity control of AUV(1) phase transitions in a system of self-driven particles[J]. Physical Review Letter,1995,75(6):1226-1229. 5结束语 [12]JADBABAIE A,LIN J,MORSE A.Coordination of groups 本文采用渐近一致性算法和虚拟结构法研究了 of mobile autonomous agents using nearest neighbor rules [J].IEEE Transactions on Automatic Control,2003,48 二维平面内多自主水下航行器小尺度编队控制问 (9):988-1001. 题,通过仿真验证了控制策略是有效的.如何将本文 [13]OLFATI-SABER R,MURRAY R.Consensus problems in 控制策略扩展到三维空间6自由度情形是下一步研 networks of agents with switching topology and time-delays 究的重点.由于所采用的一致性算法是渐近一致的, [J].IEEE Transactions on Automatic Control,2004,49 而控制律为有限时间跟踪控制,导致实际上预定编 (9):1520-1533. 队形状的形成时间为无穷大;因此如何实现有限时 [14]REN W,BEARD R.Consensus seeking in multi-agent 间一致性以及有限时间跟踪控制同步时刻的一致, systems under dynamically changing interaction topologies [J].IEEE Transactions on Automatic Control,2005,50 也是值得研究的问题 (5):655661. 参考文献: [15 KOLMANOVSKY H,MCCLAMROCH N.Developments in nonholonomic controls systems[J].IEEE Control Sys- [1]FIORELLI E,LEONARD N,BHATTA P,et al.Multi- tem Magazine,1997,15(6):20-36. AUV control and adaptive sampling in Monterey Bay[J]. [16]HONG Yiguang,XU Yangsheng,HUANG Jie.Finite-time IEEE Jourmal of Oceanic Engineering,2006,31(4):935- control for robot manipulators[J].Systems Control Let- 948. ters,2002,46(4):243-253. [2]YU S,URA T.A system of multi-AUV interlinked with a 作者简介: smart cable for autonomous inspection of underwater struc- 袁健,男,1980年生,博土研究生, tures[J].Interational Journal of Offshore and Polar Engi- 主要研究方向为网络化机器人系统编 neering,2004,14(4):264-272. 队控制,发表学术论文10余篇. [3]YU S,URA T.Experiments on a system of multi-AUV in- terlinked with a smart cable for autonomous inspection of un- derwater structures J].International Journal of Offshore and Polar Engineering,2004,14(4):273-283. [4]XIANG X.Coordinated control for multi-AUV systems based on hybrid automata[C]//Proceedings of IEEE Inter- 唐功友,男,1953年生,教授,博士 national Conference on Robotics and Biomimetics.Sanya, 生导师,EE高级会员,山东省自动化 China,2007:2121-2126. 学会常务理事等.主要研究方向为计算 [5]TANGIRALA S,KUMAR R,BHATTACHARYYA S,et 机控制、非线性控制、网络控制系统.承 al.Hybrid-model based hierarchical mission control archi- 担国家自然科学基金、“863”计划子课 tecture for autonomous underwater vehicles[C]//American 题以及省级科研基金等科研项目10余 Control Conference.Portland,USA,2005:668-673. 项.曾获国家教委科技进步一等奖1项,国家教委(教育部) [6]YANG E,GU D.Nonlinear formation-keeping and mooring 科技进步二等奖3项,中国出版协会“优秀学术专著一等 control of multiple autonomous underwater vehicles J]. 奖”1项,山东省第二届优秀科技成果二等奖1项,以及中国 IEEE/ASME Transactions on Mechatronics,2007,2 (2): 海洋大学科技进步二等奖1项等多项荣誉.发表学术论文 164-178. 100余篇,其中被SC、EI检索60余篇,出版专著1部. [7]KALANTAR S,ZIMMER U.Distributed shape control of