
第6卷第6期 智能系统学报 Vol.6 No.6 2011年12月 CAAI Transactions on Intelligent Systems Dec.2011 doi:10.3969/i.issn.1673-4785.2011.06.007 模糊c-均值算法和万有引力算法求解模糊聚类问题 谷文祥,郭丽萍,殷明浩 (东北师范大学计算机科学与信息技术学院,吉林长春130117) 摘要:针对单纯使用模糊c-均值算法(CM)求解模糊聚类问题的不足,首先,提出一种改进的万有引力搜素算法, 通过一定概率按照不同方式对速度进行更新,有效增大了种群的搜索域.其次,提出了模糊万有引力搜索算法(G SA).最后,在模糊万有引力搜索算法(FGSA)和模糊c-均值算法(PCM)的基础上,提出了一种新算法(FGSAFCM)来 求解模糊聚类问题,有效避免了单纯使用模糊©-均值算法时对初始值敏感且易于陷入局部最优的缺点.采用目标函 数和有效性评价函数作为评价标准,选取10个经典数据集作为测试数据,实验结果表明,新算法比单一的模糊c-均 值算法有更高的准确性和鲁棒性。 关键词:模糊聚类:模糊c-均值算法;万有引力搜索算法:模糊万有引力搜索算法 中图分类号:TP301.6文献标志码:A文章编号:16734785(2011)06052006 A solution for a fuzzy clustering problem by applying fuzzy c-means algorithm and gravitational search algorithm GU Wenxiang,GUO Liping,YIN Minghao (Department of Computer Science and Information Technology,Northeast Normal University,Changchun 130117,China) Abstract:Aiming at fixing the shortcomings of using fuzzy C-means algorithm solely to solve fuzzy clustering prob- lems,first,this paper proposed an improved gravitational search algorithm by updating the velocity of individuals according to a probability,expanding the search space effectively.Secondly,a fuzzy gravitational search algorithm (FGSA)was proposed.Finally,a novel hybrid algorithm(FGSAFCM)based on a fuzzy improved gravitational search algorithm (FGSA)and fuzzy c-means algorithm (FCM)was proposed to solve fuzzy clustering problems. Fuzzy c-means algorithm is very sensitive to initialization and easily gets into local optima,but the new algorithm may avoid these shortcomings.This paper chooses the objective function and validity function as the evaluation cri- terion.The FGSAFCM was tested on ten classic datasets,and the experiment results show that the new algorithm is more accurate and robust than the sole fuzzy c-means algorithm. Keywords:fuzzy clustering problem;fuzzy c-means algorithm;gravitational search algorithm;fuzzy gravitational search algorithm 聚类分析是中非监督模式识别的一个重要分 ” 模糊聚类方法[21把Zadeh的模糊理论引入到聚类 支.它试图将数据分成几个不同的组,要求组内的数 中,使每个样本对各个类别的隶属度扩展到[0,1] 据相似性大,组间的数据相似性小,这样的组在聚类 区间,这种方法在处理各类别之间含有交集的聚类 中被称为“簇”.目前,求解聚类问题主要包括硬聚 问题时,效果明显优于硬聚类方法.可能性聚类] 类、模糊聚类、可能性聚类3种方法.硬聚类方法四 方法在模糊聚类方法的基础上,不再限定样本对每 在分类时具有绝对性,即“非此即彼”,这种方式虽 个类别的隶属度之和为1. 然时间消耗非常少,但是也割断了数据之间的联系。 模糊c-均值算法(fuzc-means algorithm, FCM)[2]是求解模糊聚类问题最经典的算法之一 收稿日期:2011-06-15. 然而,模糊c-均值算法对初始值非常敏感,而且很容 基金项目:国家自然科学基金资助项目(60803102,61070084) 易陷入局部最优.万有引力算法(gravitational search 通信作者:郭丽萍.E-mail:uolp281@nenu.cdu.cn

第6期 谷文祥,等:模糊c均值算法和万有引力算法求解模糊聚类问题 ·521· algorithm,GSA)[41是由Rashedi和Nezamabadi-pour 这里,评价算法的收敛条件包括2个,一个是达 在2009年提出来的一种模拟物理学中的万有引力 到算法设定的最大迭代次数,另一个是目标函数 进行优化的新算法.它通过群体中各微粒之间的万 (4)的值在指定迭代次数内无法再变小. 有引力来指导整个种群的搜索.实验证明,万有引力 搜索具有较强的全局搜索能力.本文首先利用万有 2万有引力搜索算法 引力算法找到较好的初始解,然后用模糊c-均值算 2.1标准的万有引力搜索算法 法进行深人搜索,最终找到较优的解。 万有引力搜索算法4,B1(gravitational search al- gorithm,GSA)是2009年由Rashedi等提出的,该算 1模糊c-均值算法 法模拟物理学中的万有引力定律“宇宙中任意2个 模糊c-均值算法2,56是由J.C.Bezdek等人 质点之间存在吸引力,该引力的大小与它们质量的 于1973年提出的,该算法试图把n个数据0={01, 乘积成正比,与它们之间的距离成反比”,通过个体 02,…,,…,0n}分成k(11)是一个调节聚类结果的模糊程度的 体j之间的欧氏距离, 参数,m越大,聚类的结果就越模糊.FCM算法可以 R(t)=‖X(t),X(t)‖2 描述如下: 个体i在第d维空间上受到其他个体的合力表示为 1)选定m,初始化迭代次数t及隶属度矩阵元 素wg,i=1,2,…,n=1,2,…,k. F(t)=∑rand,F(t). j=1*i 2)按照式(5)计算聚类中心: 式中:rand是一个[0,1]区间内的随机数,增加了算 法的随机性。 3= 5) 个体i在第d维空间上的加速度按照式(7)计 算得出: 3)计算每个样本数据到各个簇的欧氏距离: F;(t) (7) dg=‖o:-‖. a(t)=M.(t) 4)对于任意的i和1,如果d>0,则按照式(6) 式中:M:(t)表示个体i的惯性质量.个体i的位置 更新隶属度, 按照式(8)进行更新: (t +1)rand;x v;(t)a (t), (6) x(t+1)=x(t)+(t+1). (8) 式中:(t)是个体i在第d维空间上的速度,x(t) 否则,如果存在d=0,则u1=1,且对于任意的j≠ 是个体i在第d维空间上的位置,rand:是一个[0, 1,g=0. 1]区间内的实数,可以增强算法的随机搜索能力. 5)如果算法仍未收敛,转2). G是万有引力常量G的初始值,随着迭代次数

·522· 智能系统学报 第6卷 的增加,G会逐渐减小来控制搜索的精确性.G是关 行c列的矩阵来表示,并按照如下方式进行更新:随 于Go和t的一个函数: 机生成一个[0,1]区间内的实数r,若r<0.5,则 c)=c()×(}B<1 (t④1)=rand:☒(t)④a(t).(13) 否则, 引力质量和惯性质量通过适应度函数计算得 v(t⊕1)=-rand:☒t(t)⊙a(t),(14) 出,假设引力质量和惯性质量相同,通过如式(9)更 x(t④1)=x(t)⊕(t⊕1).(15) 新个体的引力质量和惯性质量: 式中:④、Θ和⑧分别表示矩阵加法、减法和乘法运 M=Mg=Mi=M,i=1,2,…,N, 算.更新结束之后,可能会有些元素违背式(2)、(3) fit;(t)-worst(t) m(t)=best(t)-worst(t)' 中的约束,则需要对其进行标准化,标准化过程如下: 1)如果矩阵中的元素为负,就把该元素赋为0; M: m:(t) (9) 2)如果矩阵中的某一行元素全为0,则用[0, ∑m(回 1]区间内的随机实数重新对其进行赋值; 式中:t(t)表示个体i在时间t的适应度值, 3)如果矩阵中的所有元素都不违背约束,则按 best(t)和worst(t)定义如式(10): 如式(16)进行转换: best(t)=min fit(t), je{1,2,…,W} h/∑jhe∑jh…h/∑jh worst()). (10) 2.2改进的万有引力搜索算法 X= /∑j∑=hy…/∑- 为了增强算法的全局搜索能力,本文提出了一 种新的速度更新方式:首先,随机生成一个[0,1]区 Lh/∑jha/∑jh…h∑h 间的实数r,如果r<0.5,就按照式(8)对速度进行 (16) 更新,否则,按照式(11)更新速度: 在FGSA算法中,采用式(4)作为适应度函数, (t+1)=-rand:×(t)-a(t).(11) 适应度函数的值越小,解的质量也越高.FCSA算法 实验结果表明,这种方式能够有效地扩大了算 求解模糊聚类问题的流程如下: 法的搜索域,对于避免算法陷入局部最优值有一定 1)初始化最大迭代次数maxt及其他参数; 效果 2)生成初始种群,初始化种群中每个个体的位 2.3模糊万有引力搜索算法 置和速度; Pang等7在2004年提出了一种修改的粒子群 3)按照式(5)计算聚类中心; 算法(particle swarm optimization,PSO)用于求解旅 4)按照式(4)计算适应度函数值; 行商问题(traveling salesman problem,TSP),它采用 5)更新G; 粒子的位置和速度表示变量之间的模糊关系.本文 6)为每个个体更新惯性质量; 把这种方法用在万有引力搜索算法中来求解模糊聚 7)计算每个个体受到的合力F及加速度a; 类问题,提出了模糊万有引力搜索算法(fuz四grai- 8)按照式(13)~(15)更新每个个体的位置和 tational search algorithm,FGSA). 速度; 在FGSA中,用粒子的位置矩阵X表示样本和 9)重复3)~8),直到满足算法的停止条件. 簇之间的隶属程度.X的形式化表示如式(12): 1112 3混合新算法求解模糊聚类问题 X= 21儿22 (12) 和FGSA算法相比,FCM算法由于需要的参数 少,所以它的收敛速度比FGSA快,但是它也很容易 式中g表示个体i属于簇j的程度,它必须满足式 陷入局部最优值;FGSA算法由于出色的全局搜索 (1)~(3)的约束条件.这样,就把粒子的位置和隶属 能力,往往能找到较好的解.因此,在FCM算法和 度矩阵对应起来,每个粒子的位置和速度均由一个n FGSA算法的基础上,设计了一种新的算法一FG

第6期 谷文祥,等:模糊c均值算法和万有引力算法求解模糊聚类问题 ·523· SAFCM算法.在FGSAFCM算法中,算法初期采用 度等13个特征;CMC源于1987年印尼的避孕调 FGSA算法寻找较好的初始解,然后利用F℃M算法 查,根据社会统计学特征将被调查者分为未避孕、长 进行深入搜索.该算法继承了FCSA和FCM算法的 期避孕和短期避孕3类;Vowel包括6种不同类型 优点,有效避免了对初始值敏感和易于陷入局部最 的印度泰卢固语元音发音,每种包含3个特征;VC 优的缺点 是Henrique在一次医学研究中整理出来的,他根据 在FGSAFCM算法中,每个个体的位置由一个n 6个生物学特征将脊柱数据分为正常、椎间盘突出、 行c列的矩阵表示,第i行第j列的元素表示样本i 脊椎前移3类;TAE是威斯康星大学麦迪逊分校整 属于簇j的程度,在存储时,把每个个体的位置转换 理的关于151个助教的授课评估情况,根据5个评 成一个行向量表示.结构图如图1. 价指标将结果分为低、中、高3类.数据集的详细描 xi2…xe…xaa…w 述见表1. 表1数据集描述 图1 FGSAFCM算法中的个体结构图 Table 1 The description of datasets Fig.1 The presentation of an object in FGSAFCM FGSAFCM算法求解模糊聚类问题的流程如下: 数据 类别数特征数 数据集大小(类别大小) 集名称 1)初始化最大迭代次数maxt及其他参数; ArtSetl 3 2 300(100,100,100) 2)生成初始种群,初始化每个个体的位置和速度; ArtSet2 3 300(100,100.100) 3)设置迭代次数:Gen1=Gen2=Gen3=0; Iris 3 150(50.50,50) 4)FGSA算法). Cancer 2 9 683(444,239) ①利用FGSA算法更新种群的每个个体; Glass 6 0 214(70,76,17,13,9,29) ②Gen2=Gen2+1;如果Gen2<8,转4); 5)对每个个体i: Wine 3 13 178(59,71,48) ①个体i的位置对应于样本和簇之间的隶属度; CMC 0 1473(629.334,510) ②用FCM算法更新聚类中心; Vowel 6 3 871(72,89,172,151,207,180) ③Gen3=Gen3+1;如果Gen3<4,转5); VC 3 6 310(100,60,150) 6)Gen1=Gen1+1;如果Gen1<maxt,转4). TAE 3 5 151(49,50,52) 4仿真实验 4.2实验结果 实验参数设置:FCM算法中,m的值设置为2, 实验环境为:Pentium2.0Gz处理器,1.00GB 最大迭代次数maxt为lO0;FGSAFCM算法中,种群 内存,采用Visual Studio2008编码, 数目设置为20,万有引力常量初值G0为100,最大 4.1数据集 迭代次数为20.实验结果为10次独立实验的平均 实验数据包括ArtSet1、ArtSet2、Fisher's Iris、 值.为了更全面地测试新算法的性能,引入了有效性 Breast-Cancer-Wisconsin(Cancer)、Glass、Wine、Con- 评价函数(PC)Partition Coefficien] traceptive Method Choice (CMC)VowellsTeaching 该函数的形式化描述为 Assistant Evaluation TAE)Vertebral Column (VC)[4]10个数据集这些数据集涵盖了低维、中 'e(U)= n 维、高维的不同数据,具有一定的代表性 P℃的值越大,分类的有效性就越大.表2和表 ArtSet1和ArtSet2是2个人造数据集;Iis包括 3分别是FCM算法和FGSAFCM算法的目标函数 3类鸢尾花,每类包含萼片长、萼片宽、花瓣长和花 值、有效性评价函数值的实验结果对比.从表2和表 瓣宽4个特征;Cancer通过细胞大小、细胞形状、核 3可以看出,无论是目标函数值,还是有效性函数 染色质等9个特征,将癌症分为恶性和良性2类; 值,FGSAFCM算法都要优于FCM算法,并且随着数 Glass通过折射率、钠、镁、铝等9个特征把玻璃分为 据集维数的增加,这种优越性更加明显,充分体现了 6类;Wine分为3类,包括酒精、苹果酸、花青素、色 新算法的有效性和鲁棒性
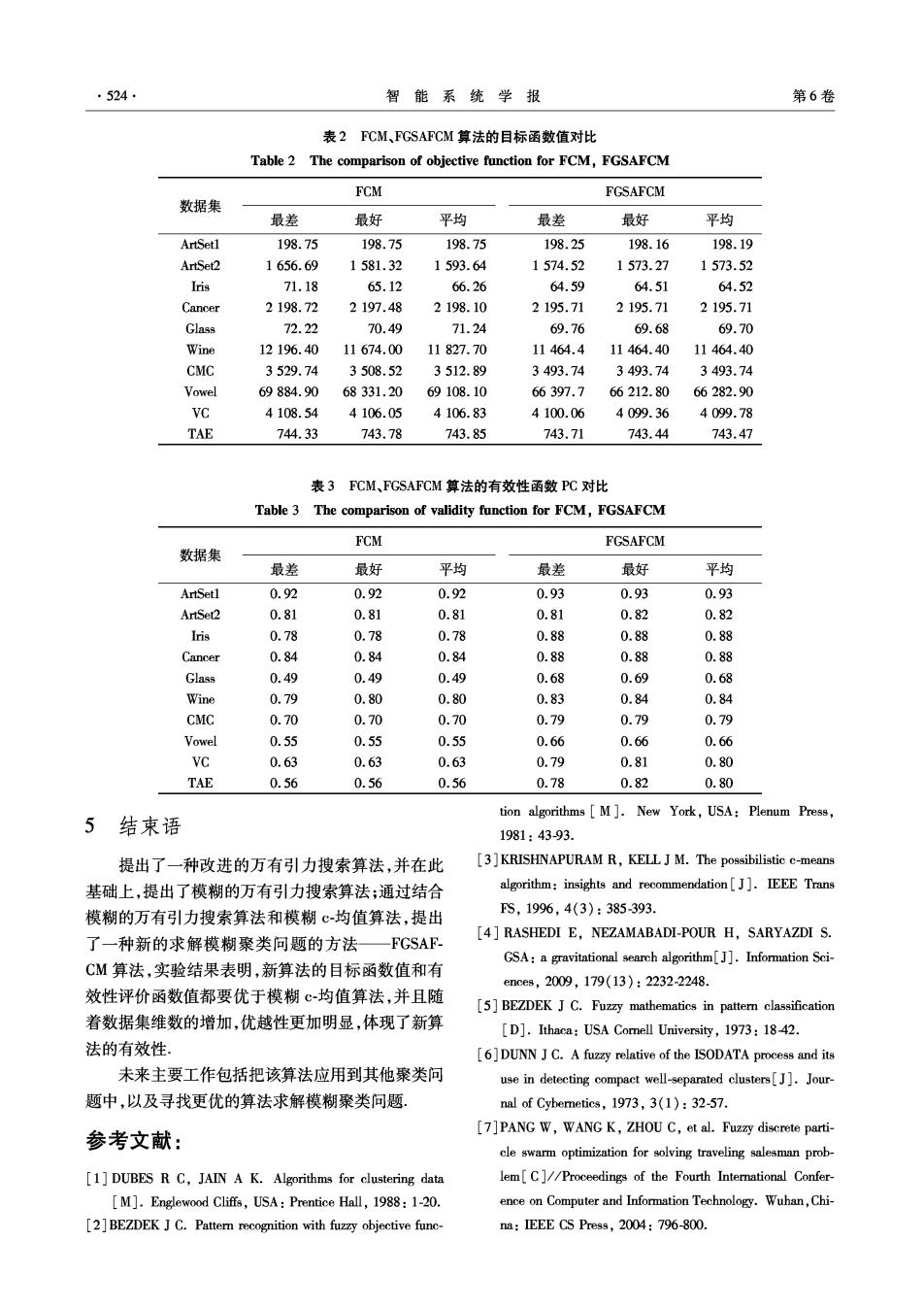
·524 智能系统学报 第6卷 表2FCM、FGSAFCM算法的目标函数值对比 Table 2 The comparison of objective function for FCM,FGSAFCM FCM FGSAFCM 数据集 最差 最好 平均 最差 最好 平均 ArtSetl 198.75 198.75 198.75 198.25 198.16 198.19 ArtSet2 1656.69 1581.32 1593.64 1574.52 1573.27 1573.52 Iris 71.18 65.12 66.26 64.59 64.51 64.52 Cancer 2198.72 2197.48 2198.10 2195.71 2195.71 2195.71 Glass 72.22 70.49 71.24 69.76 69.68 69.70 Wine 12196.40 11674.00 11827.70 11464.4 11464.40 11464.40 CMC 3529.74 3508.52 3512.89 3493.74 3493.74 3493.74 Vowel 69884.90 68331.20 69108.10 66397.7 66212.80 66282.90 VC 4108.54 4106.05 4106.83 4100.06 4099.36 4099.78 TAE 744.33 743.78 743.85 743.71 743.44 743.47 表3FCM、FGSAFCM算法的有效性函数PC对比 Table 3 The comparison of validity function for FCM,FGSAFCM FCM FGSAFCM 数据集 最差 最好 平均 最差 最好 平均 ArtSetl 0.92 0.92 0.92 0.93 0.93 0.93 ArtSet2 0.81 0.81 0.81 0.81 0.82 0.82 Iris 0.78 0.78 0.78 0.88 0.88 0.88 Cancer 0.84 0.84 0.84 0.88 0.88 0.88 Glass 0.49 0.49 0.49 0.68 0.69 0.68 Wine 0.79 0.80 0.80 0.83 0.84 0.84 CMC 0.70 0.70 0.70 0.79 0.79 0.79 Vowel 0.55 0.55 0.55 0.66 0.66 0.66 VC 0.63 0.63 0.63 0.79 0.81 0.80 TAE 0.56 0.56 0.56 0.78 0.82 0.80 tion algorithms M].New York,USA:Plenum Press, 5 结束语 1981:4393. 提出了一种改进的万有引力搜索算法,并在此 [3]KRISHNAPURAM R,KELL J M.The possibilistic c-means 基础上,提出了模糊的万有引力搜索算法;通过结合 algorithm:insights and recommendation[J].IEEE Trans 模糊的万有引力搜索算法和模糊c-均值算法,提出 FS,1996,4(3):385-393. [4]RASHEDI E,NEZAMABADI-POUR H,SARYAZDI S. 了一种新的求解模糊聚类问题的方法—FGSAF GSA:a gravitational search algorithm[J].Information Sci- CM算法,实验结果表明,新算法的目标函数值和有 ences,2009,179(13):2232-2248. 效性评价函数值都要优于模糊c-均值算法,并且随 [5]BEZDEK J C.Fuzzy mathematics in pattern classification 着数据集维数的增加,优越性更加明显,体现了新算 D].Ithaca:USA Comell University,1973:18-42 法的有效性, [6]DUNN J C.A fuzzy relative of the ISODATA process and its 未来主要工作包括把该算法应用到其他聚类问 use in detecting compact well-separated clusters[J].Jour- 题中,以及寻找更优的算法求解模糊聚类问题. nal of Cyberetics,1973,3(1):32-57. [7]PANG W,WANG K,ZHOU C,et al.Fuzzy discrete parti- 参考文献: cle swarm optimization for solving traveling salesman prob- [1]DUBES R C,JAIN A K.Algorithms for clustering data lem[C]//Proceedings of the Fourth Interational Confer- [M].Englewood Cliffs,USA:Prentice Hall,1988:1-20. ence on Computer and Information Technology.Wuhan,Chi- 2]BEZDEK J C.Pattern recognition with fuzzy objective func- na:IEEE CS Press,2004:796-800

第6期 谷文祥,等:模糊c均值算法和万有引力算法求解模糊聚类问题 ·525· [8]PAL S K,DUTTA M R D.Fuzzy sets and decision making School of Information and Computer Science,2007 approaches in vowel and speaker recognition[J].IEEE 作者简介: Transactions on Systems,Man,and Cybernetics,1977,7 谷文祥,男,1947年生,教授,博士 (8):625629. 生导师,主要研究方向为智能规划与规 [9]BEZDEK J C.Cluster validity with fuzzy sets[]Cyber- 划识别、形式语言与自动机理论、模糊 netic8,1974,3(3):58-73. 数学及其应用.主持国家自然科学基金 [10]RUNKLER T A,KATE C.Fuzzy clustering by particle 项目3项,发表学术论文100余篇. swarm optimization [C]//International Conference on Fuzzy Systems Vancouver Canada,2006:601-608. [11]WANG Yingje.Fuzzy clustering analysis by using genetic 郭丽萍,女,1989年生,硕士研究 algorithm[J].ICIC,2008,2(4):331-337. 生,主要研究方向为智能规划、智能信 [12]MAULIK UJJWAL,BANDYOPADHYAY SANGHAM-ITA. 息处理. Genetic algorithm-based clustering technique[J].Pattem Rec0 gnition,2000,33(9):1455-1465. [13]谷文祥,李向涛,朱磊,等.求解流水线调度问题的万 有引力搜索算法[J].智能系统学报,2010,5(5): 411-418. 殷明浩,男,1979年生,副救授,主 GU Wenxiang,LI Xiangtao,ZHU Lei,et al.A gravita- 要研究方向为智能规划与自动推理.主 tional search algorithm for flow shop scheduling[J].CAAI 持参与多项西家自然科学基金项目.发 Transactions on Intelligent Systems,2010,5(5):411- 表学术论文30余篇,其中大部分被$CI 和EI检索. 418. [14]ASUNCION A,NEWMAN D J.UCI machine leaming re- pository[DB/OL].Irvine,USA:University of Califomia, 第4届智能人机系统与控制论国际会议(IHMSC2012) The 4th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC 2012) As a continuation of IHMSC 2009 to IHMSC 2011,which were held successfully in Hangzhou,Nanjing and Hangzhou re- spectively,the 4th Interational Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC 2012)will take place at Jiangxi Normal University in Nanchang,China,between 26-27 August,2012.The aim of this conference is to provide a forum for exchanges of research results,ideas for and experience of application among researchers and practi- tioners involved with all aspects of human-machine systems and cybemetics. Publication The proceedings of IHMSC 2012 will be published by the IEEE Computer Society's Conference Publishing Service (CPS),and indexed by EI and ISTP.The proceedings of previous three IHMSC from 2009 to 2011 have been indexed by EI and ISTP,and included in the digital libraries (CSDL,IEEE Xplore,IEEE IEL). Website:http://ihmsc.zju.edu.cn/
殷明浩,男,1979年生,副教授,主 要研究方向为智能规划与自动推理.主 持参与多项国家自然科学基金项目.发 表学术论文30余篇,其中大部分被SCI 和EI检索