
第7卷第2期 智能系统学报 Vol.76.2 2012年4月 CAAI Transactions on Intelligent Systems Apr.2012 D0I:10.3969/i.issn.16734785.201111008 网络出版t地址:htp://www.cnki.net/kcma/detail/23.1538.TP.20120309.1559.005.html 双层隐马尔可夫链的突发流合成 谢逸,唐成华2,黄向农3 (1.中山大学信息科学与技术学院,广东广州510006;2.桂林电子科技大学,计算机科学与工程学院,广西桂林 541004;3.中山大学网络与信息技术中心,广东广州510275) 摘要:网络流模型被广泛用于构建网络与网络服务的测试环境,其准确性直接影响各种业务的性能评估结果及在 实际网络环境中的鲁棒性.随着电子商务及新型网络应用的普及,突发流现象已经成为现代互联网的主要特征之 一.针对平稳网络流而设计的传统网络流模型已经难以有效地描述现代网络中突发流的时间结构性及统计属性,从 而不能准确反映现代网络流的行为特征.为此,提出一种新的结构化双层隐马尔可夫模型用于模拟实际网络环境下 的突发流,并设计了有效的模型参数推断算法及突发流合成方法.该模型通过结构化的2层隐马尔可夫过程描述突 发流并实现仿真合成,使合成流可以重现实际突发流的时间结构性、统计特性及自相似性.实验表明,该模型可以有 效合成突发流 关键词:隐马尔可夫模型;合成;突发流;网络 中图分类号:TP30文献标志码:A文章编号:1673-4785(2012)02-010807 A doubly hidden Markov model for synthesizing bursty workloads XIE Yi',TANG Chenghua2,HUANG Xiangnong' (1.School of Information Science and Technology,Sun Yat-Sen University,Guangzhou 510006,China;2.School of Computer Sci- ence and Engineering,Guilin University of Electronic Technology,Guilin 541004,China;3.Network and Information Technology Center,Sun Yat-Sen University,Guangzhou 510275,China) Abstract:Network traffic models have been widely used to build the test environment for networks and network services.Their accuracy directly impacts the performance evaluation results of various services and their robustness in the actual network environment.With the popularity of e-commerce and new network applications,the burst traf- fic phenomenon has become one of the main features of the modern internet.Traditional traffic models designed for stationary network traffic have difficulty in effectively describing the temporal structure and statistical properties of burst traffic of modern networks,which causes them not to be able to accurately reflect the actual network environ- ment.In this paper,a new structural doubly hidden Markov model was proposed to characterize the practical burst traffic in a real network environment.Efficient algorithms for inference of model parameters and synthesis of the burst workload were also introduced.Based on the hierarchical structure,the proposed model can reproduce the similar temporal structure,statistical properties,and self-similarity of the real burst traffic.The proposed model in- cludes two hidden Markov processes.The parent Markov state process was used to describe the large-scale trends or phases of burst traffic.The child Markov process was used to describe the small-scale fluctuations that happen dur- ing a given phase of the arrival process.Experiments were implemented to validate the proposed model. Keywords:hidden Markov model;synthesize;burst workload;network 网络流模型一直是互联网研究中的一个重要 领域.一个有效的流模型是实现性能测试、容量规划 及攻击防御的基础.没有正确的网络流模型,将难以 收稿日期:2011-11-14.网络出版日期:20120309 准确预测网络性能指标的变化,从而无法使网络及 基金项目:国家自然科学基金资助项目(60970146);教育部博士点专 项基金资助项目(20090171120001);中央高校基本科研业 其业务实现自适应调整.因此,网络流模型对互联网 务费专项资金资助项目(11P38). 通信作者:谢逸.E-mail:xieyi5@mail.sysu.edu.cm. 及各种业务的研究与设计都具有重要的意义·

第2期 谢逸,等:双层隐马尔可夫链的突发流合成 ·109· 建立有效网络流模型的前提是了解网络流的属 络流.这些方法主要有三方面的问题:1)已有的随 性特征.已有的研究12]已经指出,大部分网络流具 机过程流模型采用平板结构,因此难以描述具有不 有自相似性、长相关性及突发性.其中,突发流是指 规则、宽变化特性的突发流:2)由于模型参数在估 数据传输中的非平衡模式,即网络流在某些时候呈 计阶段受整个流过程的影响,它们难以刻画“突发” 现出非常高的数据传输率,而在另外一些时间则非 或“非突发”阶段的局部细节的变化过程:3)这类模 常低.例如现代商务网站常常组织“抢购”或“秒杀” 型难以重构突发流的时间结构性特征,例如相邻2 活动作为其销售策略.在这些活动期间,网络流量会 个突发过程的时间间隔、突发过程的持续时间等.因 因为用户数的激增而出现暴发性增长,从而导致突 此,当实际网络流的突发性非常显著时,或网络量的 发流的出现.实际网络中的突发流不具有规律性,例 波动范围变得非常大时,这一类模型的性能将逐渐 如出现时间、持续时间、突发强度等.突发流的形成 下降,从而导致仿真流不具有实际突发流的各种特 受多种随机因素影响,例如热点新闻的发布、金融市 性.增加模型的参数,例如增加量化间隔,或增加 场的运作、大型活动的现场播放等都会引起突发流, Markov模型的状态数,可以在一定程度上提高模型 如果网络基础设施或网络服务在设计阶段没有考虑 描述细节过程的能力,但会导致两方面的问题:1) 到这种突发性现象,将有可能导致它们无法有效应 参数的增加必然导致模型的计算复杂度增加,特别 对实际网络场景中的突发流.在过去的20年中,很 是参数个数与复杂度具有非线性关系的模型;2)对 多模型被用于描述突发网络流.已有的研究工作主 某些模型,参数的增加不但不会提高性能,还可能导 要从两方面刻画突发流:结构方法与随机过程方法 致“过描述”21问题的出现 早期网络流的研究3]主要考虑结构属性,例如自 为此,提出一种新的方法用于合成突发网络流, 相似性与长相关性.在这之后,大量的数学方法被用 该方法基于多层隐马尔可夫模型(hierarchical hid- 于描述网络流的自相似性与长相关性,例如经典的 den Markov model,HHMM).HHMM1s]已经成功应 On/Of模型4]、M/G/e模型I、小波模型s]、分形 用于不同的领域,例如文本识别、策略识别、活动识 布朗运动模型[6]等.结构化方法主要存在两方面的 别、视频分析、图像分类和信息抽取等.与经典的隐 问题:1)它们无法描述时间域信息(例如时间结构 马尔可夫模型(hidden Markov model,HMM)[4]相 性),因此这类模型无法正确重构实际突发流的时 比,这些HMM模型最主要的特点是,通过增加一 间特性;2)几乎所有描述自相似性的模型都仅通过 个隐马尔可夫链描述慢变化的高层活动,从而捕获 个共同的参数Hust来描述网络流的突发性.而 自然序列的长期相关性.这一特征使HHMM适合描 实际的网络流往往具有宽尺度的变化范围,使用单 述非平稳的突发网络流.然而从目前收集到的文献 一参数的结构化方法不足以刻画复杂的、多尺度的 看,HHMM的这一优点还没有被应用到网络流建模 突发流.例如,理论上的尺度范围存在于(0,∞) 上.本文的主要创新点包括:1)通过改进模型的结 中.然而,实际表现出来的多尺度性往往只有有限的 构,而不是通过增加模型参数来提高突发流的模拟 范围,而且无法精确表示.另外,现有的自相似模型 性能.2)首次采用基于HHMM的结构化隐马尔可夫 往往假设所有的矩序(moment order)的尺度指数都 模型实现突发流建模.基于该模型的合成流可以有 相同,而实际的网络流中,不同阶的尺度指数由不同 效重现实际突发流的时间结构特性、统计特性及自 的参数所控制.因此,单一的Hust参数实际上无法 相似性.3)有效的模型参数推断算法与突发流合成 精确描述多尺度的自相似性 算法,使该模型的结构优于传统平板型结构的模型, 典型的随机过程方法主要基于马尔可夫族模 但计算复杂度没有显著增加 型.在文献[4]中,基于马尔可夫模型的“0n/0”模 1建模依据与算法 型用于模拟语音信号.在文献[8]中,采用树结构隐 马尔可夫链到达模型(Markovian arrival process, 1.1模型定义 MAP)被用于描述网络流.文献[9]使用马尔可夫调 假设所观测到的时间过程是到达率过程(arrival 制泊松过程(Markov modulated Poisson process, rate process,ARP).如图1所示,从大尺度看,可以根 MMPP)描述网络流的突发性.文献[10]使用马尔可 据到达率的量级把ARP划分为不同的流量阶段(traf 夫调制流源模型(Markov-modulated fluid sources, fic phase,TP),例如低流量阶段、过渡阶段和高流量 MMS)描述网络流.文献[11]使用自回归马尔可夫 阶段.因此,ARP大尺度变化过程实际上是由不同的 模型(autoregressive Markov model,ARMM)描述网 流量阶段交替变化所组成,即ARP的粗轮廓可以通

·110 智能系统学报 第7卷 过流量阶段过程(traffic phase process,TPP)来描述. 表1列出了本文所使用的一些符号及定义.为 而TPP本身也是一个时间过程.与一般基于Markov 了便于介绍下文的算法,使用i了表示Q中的元素, 模型的时间序列建模类似,假设流量阶段过程TPP满 即父状态集合中的马尔可夫状态;用m、n表示Q 足马尔可夫假设的无后效性.因此PP可以用一个马 中的元素,其中i∈Q,与q分别表示父状态过程 尔可夫链来描述.该马尔可夫链称为父马尔可夫过 与子状态过程在t时刻的状态.于是可以使用图2 程,包含Q1个状态,每一个状态对应一种典型的流 所示的双层隐马尔可夫状态图来表示突发流的到达 量阶段TP.在给定的流量阶段i内(或父状态i下), 过程。 局部的小尺度网络流波动由另一个嵌套的子马尔可 表1模型符号定义 夫链描述.该嵌套的子马尔可夫链包含1QI个有效状 Table 1 Notation of symbols 态及一个吸收态⊙,每一个子状态对应一种典型的 符号定义 局部流量分布.因此,双重马尔可夫模型可以描述网 0 0={01,02,…,0r},长度为T的到达率序列 络流的大尺度及小尺度变化过程 0 t时刻的到达率 31510 xeb={x。,。+1,…,},时间跨度为a到b的时 。5 间序列 9 6 Q Q={1,2,…,1Q1},父马尔可夫状态集合 ×10 Q=11,2,…,1Q1,⊙引,父马尔可夫状态i的子 4.014.02 4.034.044.054.064.07 Q 马尔可夫状态集合,其中⊙表示吸收态。 时间结构/min ■P[=],父马尔可夫链初始状态概率 图1大尺度网络流量阶段 Fig.1 Large-scale typical phase of arrival rate process a哈=P[=jlg-1=门,父马尔可夫链状态转移概 a喝 该模型的随机性及状态的隐藏性在于:1)流量 率 阶段TP无法被准确测量,例如流量阶段的开始时 交% π■P[g=ml=i,-1≠],父马尔可夫状态i 间、持续时间等;2)在给定的流量阶段内,小尺度的 下,子状态链的初始概率 局部波动仍然具有随机性:3)一个观测到的到达率 (或ARP片段)有可能来自于不同的流量阶段、或来 a a=P[g=nlgi-1=m,-:t=],父马尔可夫 状态i下,子状态链的转移概率 自于同一个父状态下不同的子状态.因此,在这个双 层马尔可夫模型中,父马尔可夫链和子马尔可夫链 b b=P[0,=k|g=m,=i],父马尔可夫状态i 下,子状态链的输出概率 都具有不确定性与隐藏性,它们无法被精确测量,只 能通过可观测的ARP进行估计.可见双层马尔可夫 入={,喝,π,a,b},模型的参数集合. 模型可以看成一个简化的HHMM:1)父状态链不可 观测,但控制子状态过程;2)子状态过程不可观测, 但控制模型的输出过程.模型的参数(即父/子状态 过程的初始概率、状态转移概率及子状态的输出概 率)代表网络流的内部形成机制.为了使用HHMM 构建上述双层隐马尔可夫模型,做了以下假设: 1)父状态的跳转将使当前子状态过程结束,并 触发一个新的子状态过程开始; 2)每个子状态集中的吸收态不输出观测值,但 吸收态出现时,当前子状态过程将结束并返回父状 态过程; 3)模型的输出仅由子状态链控制,且相同子状 态下的输出相互独立; 图2突发网络流的状态 Fig.2 A state diagram for describing the burst traffic 4)不同父状态下的子状态集合可以具有不同 父马尔可夫过程最初以概率进入状态.状 的子状态数

第2期 谢逸,等:双层隐马尔可夫链的突发流合成 ·111· 态i以概率π生成其子状态m.然后,在父状态i 的初始值为 下的子状态根据概率b输出当前的到达率·完 Br(i,m)=1. 成输出以后,子状态m按照转移概率分布α跳转 为了推断双层隐马尔可夫模型的参数,定义一 到下一个子状态,然后重复模型的输出与子状态 个辅助的联合概率密度函数,(i,j,m,n)并给出其 的跳转.当子状态过程出现吸收状态⊙时,模型将 递推公式: 停止当前的子状态过程并返回父马尔可夫状态,由 5.(ij,m,n)=P[or,(q,9)= 父状态过程的状态转移概率决定下一个父状态 (i,m),(4,9*)=G,n)]= 的取值,通过这种方式,网络流可以被分割为连续的 a(i,m)B,),i≠j 流量阶段过程并由父马尔可夫状态过程描述,每一 个阶段(父状态)代表不同的流量等级.而每一个特 La(i.m)(i)i-j 定流量阶段中的小尺度网络流波动则由相应的子状 定义辅助联合概率密度函数Y,(i,m)及其递推 态过程的转移概率及输出概率来刻画.因此,双层隐 公式为 马尔可夫链非常适合描述网络流,特别是非平稳的 Y(i,m)=P[our,g2=i,q:=ml A] 突发流过程. £(,m,. 1.2模型参数推断及突发流合成 基于上述的递推过程,可以估计出模型的各个 与经典的HMM类似,双层隐马尔可夫模型主 参数: 要用于解决以下3类问题:1)给定一个模型入,计算 1)父状态过程初始概率密度函数的最大或 观测序列相对于该模型的概率;2)给定一个模型入 然概率估计为 及观测序列:r,估计最可能的双层隐马尔可夫状 态序列;3)通过观测序列0:r估计模型的参数,即调 =∑m.(ij,m,n)/ 整模型的参数使1)和2)的概率最大.针对所提出 式中:W=∑,m,5(i,j,m,n)是归一化因子 的双层隐马尔可夫模型,介绍一种前后向算法解决 2)父过程状态转移概率密度函数a的最大或 上述3个问题 然概率估计为 基于提出的第3个假设条件,即模型的输出仅由 =∑∑.m,m)() 子状态链控制,且相同子状态下的输出相互独立,有 式中:N2()=∑.(ij,m,n)是归-化因子 P[osl gi =m,g =i]=P[o,I gi =m,gi =i]. 3)父状态下的子状态过程的初始概率密度函 数π的最大或然概率估计为 定义模型的前向变量: &,(i,m)=P[o,9g=i,9=m] 分=∑∑G,n,m)/N 考虑t-1时刻,模型的父状态只能是g-1=i 式中:N=-∑m,,in,m)是归-化因子. 或-1≠i,可以得到前向变量的递推过程: 4)父状态下的子状态过程的状态转移概率密 a(i,m)=∑a-(i,n)aab+ 度函数a的最大或然概率估计为 ∑a-iG,n)m =∑(i,m,m)(m). 式中:W(m)=∑Σ(i,i,m,n)是归一化因子. 对于给定的状态(i,m)及时间t>1,前向变量 5)父状态i下的子状态过程的输出概率密度函 的初始值为 a(,m)=m6 数的最大或然概率估计为 定义后向变量: =∑l∑(ij,m,n)8(o,=)/N(m). B,(i,m)=P[0+:r1q=i,4=m]. 式中:(m)=Σ,(ij,m,n)是归-化因子 考虑t+1时刻,模型的父状态只能是+1=i 6)双重隐状态链(q,9)的后验估计为 或④1≠i,可以得到后向变量的递推过程: (arg maxp[our,4i=i,gi m]= B,(i,m)=∑abnB(,n)+ arg maxy (i,m). ∑aja.B,n). 7)规测序列0:r相对于给定模型入的或然概率为 L=P[orIA]=∑P[or,=i,听=ml入]= 对于给定的状态(i,m)及时间t<T,后向变量
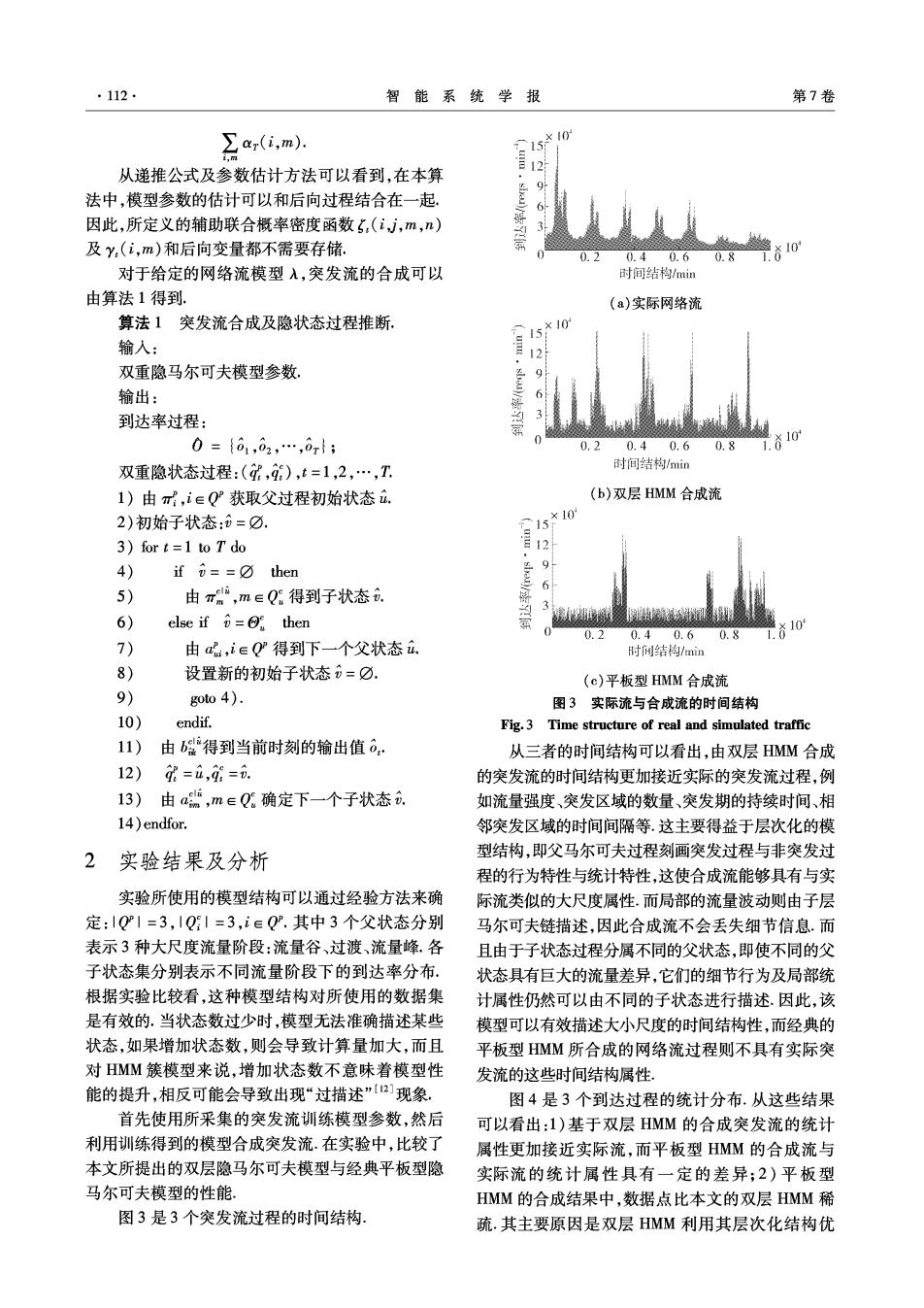
·112, 智能系统学报 第7卷 ∑ar(i,m) 5*10 从递推公式及参数估计方法可以看到,在本算 12 法中,模型参数的估计可以和后向过程结合在一起。 6 因此,所定义的辅助联合概率密度函数5(i,j,m,n) 及y,(i,m)和后向变量都不需要存储. 0.40.60.8 ǒ0 对于给定的网络流模型入,突发流的合成可以 时间结构/min 由算法1得到. (a)实际网络流 算法1突发流合成及隐状态过程推断。 输入: *o 12 双重隐马尔可夫模型参数 9 输出: 到达率过程: 0={01,02,…,0r}; 0.2 0.40.6 0.8 双重隐状态过程:(,9),t=1,2,…,T 时间结构/min 1)由,ieQ获取父过程初始状态a. (b)双层HMM合成流 2)初始子状态:=⑦. 15*l0 3)for t=1 to T do 12 4) ifi==☑then 9 6 5) 由π,meQ:得到子状态 6) else if=⑧then 10 0.2 0.40.60.8 7) 由a,ieQ得到下一个父状态a. 时问结构/mim 8) 设置新的初始子状态=⑦. (c)平板型HMM合成流 9) goto 4). 图3实际流与合成流的时间结构 10) endif. Fig.3 Time structure of real and simulated traffic 11) 由得到当前时刻的输出值6 从三者的时间结构可以看出,由双层HMM合成 12) =i,=i. 的突发流的时间结构更加接近实际的突发流过程,例 13)由a,meQ确定下一个子状态 如流量强度、突发区域的数量、突发期的持续时间、相 14)endfor. 邻突发区域的时间间隔等.这主要得益于层次化的模 2实验结果及分析 型结构,即父马尔可夫过程刻画突发过程与非突发过 程的行为特性与统计特性,这使合成流能够具有与实 实验所使用的模型结构可以通过经验方法来确 际流类似的大尺度属性.而局部的流量波动则由子层 定:1Q1=3,1Q引=3,i∈Q°.其中3个父状态分别 马尔可夫链描述,因此合成流不会丢失细节信息.而 表示3种大尺度流量阶段:流量谷、过渡、流量峰.各 且由于子状态过程分属不同的父状态,即使不同的父 子状态集分别表示不同流量阶段下的到达率分布. 状态具有巨大的流量差异,它们的细节行为及局部统 根据实验比较看,这种模型结构对所使用的数据集 计属性仍然可以由不同的子状态进行描述.因此,该 是有效的.当状态数过少时,模型无法准确描述某些 模型可以有效描述大小尺度的时间结构性,而经典的 状态,如果增加状态数,则会导致计算量加大,而且 平板型HMM所合成的网络流过程则不具有实际突 对HMM簇模型来说,增加状态数不意味着模型性 发流的这些时间结构属性. 能的提升,相反可能会导致出现“过描述”2]现象. 图4是3个到达过程的统计分布.从这些结果 首先使用所采集的突发流训练模型参数,然后 可以看出:1)基于双层HMM的合成突发流的统计 利用训练得到的模型合成突发流.在实验中,比较了 属性更加接近实际流,而平板型HMM的合成流与 本文所提出的双层隐马尔可夫模型与经典平板型隐 实际流的统计属性具有一定的差异;2)平板型 马尔可夫模型的性能, HMM的合成结果中,数据点比本文的双层HMM稀 图3是3个突发流过程的时间结构, 疏.其主要原因是双层HMM利用其层次化结构优
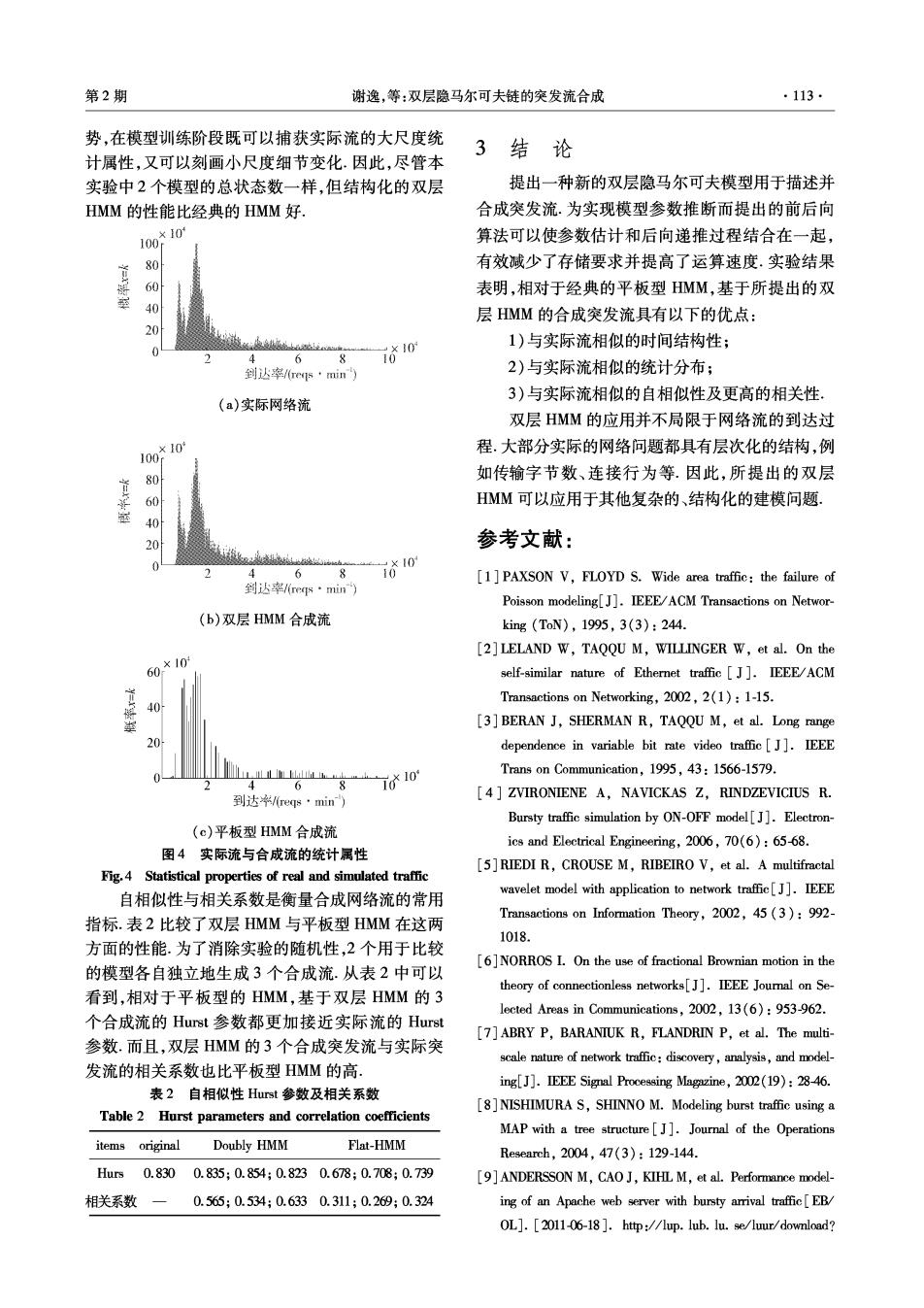
第2期 谢逸,等:双层隐马尔可夫链的突发流合成 ·113· 势,在模型训练阶段既可以捕获实际流的大尺度统 3 结论 计属性,又可以刻画小尺度细节变化.因此,尽管本 实验中2个模型的总状态数一样,但结构化的双层 提出一种新的双层隐马尔可夫模型用于描述并 HMM的性能比经典的HMM好. 合成突发流.为实现模型参数推断而提出的前后向 100,*10 算法可以使参数估计和后向递推过程结合在一起, 80 有效减少了存储要求并提高了运算速度.实验结果 60 表明,相对于经典的平板型HMM,基于所提出的双 40 层HMM的合成突发流具有以下的优点: 20 i010 1)与实际流相似的时间结构性; 4 68 到达率res·min) 2)与实际流相似的统计分布; (a)实际网络流 3)与实际流相似的自相似性及更高的相关性。 双层HMM的应用并不局限于网络流的到达过 10 程.大部分实际的网络问题都具有层次化的结构,例 100 80 如传输字节数、连接行为等.因此,所提出的双层 60 HMM可以应用于其他复杂的、结构化的建模问题. 参考文献: 0 4 68 访o [1]PAXSON V,FLOYD S.Wide area traffic:the failure of 到达率reqs·min) Poisson modeling[J].IEEE/ACM Transactions on Networ- (b)双层HMM合成流 king(ToN),1995,3(3):244. [2]LELAND W,TAQQU M,WILLINGER W,et al.On the 60.x10 self-similar nature of Ethernet traffic J].IEEE/ACM Transactions on Networking,2002,2(1):1-15. 40 [3]BERAN J,SHERMAN R,TAQQU M,et al.Long range dependence in variable bit rate video traffic[J].IEEE u LL thi w 110 Trans on Communication,1995,43:1566-1579. 8 到达*/reqs·min) [4 ZVIRONIENE A,NAVICKAS Z,RINDZEVICIUS R. Bursty traffic simulation by ON-OFF model[J].Electron- (c)平板型HMM合成流 ics and Electrical Engineering,2006,70(6):65-68. 图4实际流与合成流的统计属性 [5]RIEDI R,CROUSE M,RIBEIRO V,et al.A multifractal Fig.4 Statistical properties of real and simulated traffic 自相似性与相关系数是衡量合成网络流的常用 wavelet model with application to network traffic[J].IEEE Transactions on Information Theory,2002,45(3):992- 指标.表2比较了双层HMM与平板型HMM在这两 1018 方面的性能.为了消除实验的随机性,2个用于比较 [6]NORROS I.On the use of fractional Brownian motion in the 的模型各自独立地生成3个合成流.从表2中可以 theory of connectionless networks[J].IEEE Joural on Se 看到,相对于平板型的HMM,基于双层HMM的3 lected Areas in Communications,2002,13(6):953-962. 个合成流的Hust参数都更加接近实际流的Hurst [7]ABRY P,BARANIUK R,FLANDRIN P,et al.The multi- 参数.而且,双层HMM的3个合成突发流与实际突 scale nature of network traffic:discovery,analysis,and model- 发流的相关系数也比平板型HMM的高. ing[J].IEEE Signal Processing Magazine,2002(19):28-46. 表2自相似性Hurst参数及相关系数 Table 2 Hurst parameters and correlation coefficients [8 NISHIMURA S,SHINNO M.Modeling burst traffic using a MAP with a tree structure J].Journal of the Operations items original Doubly HMM Flat-HMM Research,2004,47(3):129-144. Hurs0.8300.835;0.854;0.8230.678;0.708;0.739 [9]ANDERSSON M,CAO J,KIHL M,et al.Performance model- 相关系数 0.565;0.534;0.6330.311;0.269;0.324 ing of an Apache web server with bursty arrival traffic[EB/ OL].[2011-06-18 ]http://lup.lub.lu.se/luur/download?

.114. 智能系统学报 第7卷 func downloadFile&recordOId =532529&fileOld =625324. 作者简介: [10]KONTOVASILIS K,MITROU N.Bursty traffic modeling 谢逸,男,1973年生,讲师,博士,主 and efficient analysis algorithms via fluid-flow models for 要研究方向为计算机网络与通信.发表 ATM IBCN[J].Annals of Operations Research,1994,49 学术论文20余篇,其中多篇被SCI、EI (1):279-323. 检索。 [11]LIU P,CHEUNG W,LI K.On the modeling of bursty traffic[C]//Proceedings on Computer,Communication, Control and Power Engineering.Beijing,China,2002: 唐成华,男,1974年生,副教授,博 220-223. 士,主要研究方向为智能信息处理、网 [12]JOHNSON M.Why doesn't EM find good HMM POS-tag- 络信息安全等,发表学术论文30余篇, gers[C]//Proceedings of the 2007 Joint Conference on 被EI检索13篇, Empirical Methods in Natural Language Processing and Computational Natural Language Learning (EMNLP-CoN- LL).Prague,Czech Republic,2007:296-305. [13]FINE S,SINGER Y,TISHBY N.The hierarchical hidden 黄向农,男,1958年生,工程师,主 Markov model:analysis and applications[J].Machine 要研究方向为计算机网络应用技术 Learning,1998,32(1):41-62. [14]RABINER L.A tutorial on hidden Markov models and se lected applications in speech recognition[].Proceedings of the IEEE,1989,77(2):257-286. 第4届智能人机系统与控制论国际会议(IHMSC2012) The 4th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC 2012) As a continuation of IHMSC 2009 to IHMSC 2011,which were held successfully in Hangzhou,Nanjing and Hangzhou re- spectively,the 4th Interational Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC 2012)will take place at Jiangxi Normal University in Nanchang,China,between 26-27 August,2012.The aim of this conference is to provide a forum for exchanges of research results,ideas for and experience of application among researchers and practi- tioners involved with all aspects of human-machine systems and cybemetics. Publication The proceedings of IHMSC 2012 will be published by the IEEE Computer Society's Conference Publishing Service (CPS),and indexed by EI and ISTP.The proceedings of previous three IHMSC from 2009 to 2011 have been indexed by EI and ISTP,and included in the digital libraries (CSDL,IEEE Xplore,IEEE IEL). Website:http://ihmsc.zju.edu.cn/