
第5卷第3期 智能系统学报 Vol.5 No.3 2010年6月 CAAI Transactions on Intelligent Systems Jun.2010 doi:10.3969/j.issn.16734785.2010.03.002 无穷概念的重新统一 何华灿,何智涛 (1.西北工业大学计算机学院,陕西西安710072;2.北京航空航天大学计算机学院,北京100191) 摘要:康托尔是用数学方法系统研究实无穷概念的第一人,为此他创立了集合论,为现代数学奠定了重要的理论 基础,但其中的连续统假设和层次实无穷观又给数学带来了许多问题.130多年来不断有人怀疑连续统假设,但一直 没有找到解决这个问题的有效办法.文章首先在图灵机基础上提出完全编码算法和完全译码算法,揭示了无穷编码 的不变性(CI原理),证明了实数可数、连续统假设不成立,实现了实无穷概念的重新统一,从根本上解决了希尔伯 特第一问题.然后进一步证明所有的无穷集都可通过自然数集变换出来,自然数集是所有无穷集的数学模型.最后 讨论了有关无穷的数学哲学问题.无穷概念的统一奠定了实无穷理论的基础,对数学、物理、逻辑、哲学和其他许多 学科都将产生广泛而深远的影响, 关键词:实无穷;图灵机;无穷编码的不变性;连续统假设;希尔伯特问题:自然数集 中图分类号:0144.1;TP18文献标识码:A文章编号:16734785(2010)030202-19 Reunifying concepts of infinity HE Hua-can',HE Zhi-tao2 (1.School of Computer Science,Northwestem Polytechnical University,Xi'an 710072,China;2.School of Computer Science, Beihang University,Beijing 100191,China) Abstract:Georg Cantor was the first person to use mathematical methods to systematically study the concept of in- finity.This work formed the basis of set theory,which in turn evolved into the primary theoretical basis for modern mathematics.However,the continuum hypothesis (CH)and the layered actual infinity view in set theory intro- duced long lasting paradoxes into modern mathematics.Over the past 130 years,many people have worked on CH, but no one has found a way to prove or disprove it.The authors proposed a solution based on the Turing machine. The complete encoding algorithm and the complete decoding algorithm revealed the infinite coding invariance (ICI principle),proving that the real number set is denumerable and CH does not hold.In this way the reunification of the concepts of infinity was established,effectively solving Hilbert's problem 1.Furthermore,it was proven that infinite sets can all be derived from the natural number set,and the natural number set is the mathematical model of all infinite sets.Finally,we discussed some problems with the mathematical philosophy of infinity.The estab- lishment of a unified concept of infinity forms the basis of an actual infinity theory.It will have a significant effect on mathematics,physics,logic,philosophy and many other scientific disciplines. Keywords:actual infinity;Turing machine;infinite coding invariance;continuum hypothesis;Hilbert's problems; natural number set 在探索实无穷概念的过程中,康托尔(G.Can- 之间没有其他的超限基数存在.CH是现行的层次 tor)根据他的实数不可数定理(o,>o)提出了连续 实无穷观的理论基石,这种无穷观认为实无穷是一 统假设(the continuum hypothesis,CH):在oo和o1 个由无穷多个大小不同的超限基数组成的系列⊙, ①1,w2,…(ω41=2)山.由于CH涉及到数学、逻 收稿日期:2010-0304. 辑和哲学中的许多基本问题,1900年希尔伯特(D. 基金项目:国家自然科学基金资助项目(60273087,60575034):西北 工业大学基础研究基金资助项目(W018101). Hilbert)把它作为20世纪需要重点解决的23个数 通信作者:何华灿.E-mail:hehuac(@gmail..com 学问题之首提了出来.1938年哥德尔(K.Gdel)证

第3期 何华灿,等:无穷概念的重新统一 ·203· 明了ZF公理集合论与CH相容.1963年柯亨(P.J. 而推翻了欧几里德(M.Eukleides)整体一定大于部 Choen)用他创立的力迫法证明ZF系统与CH相容 分的看法.在微积分理论的萌芽时期,曾经采取过纯 所以用数学公理方法不能解决CH问题,CH的真伪 粹的实无穷观,把无穷小量(infinitesimal)看成是一 至今没有结论2.但是,这些证明都是在承认①,> 个确定的特殊数.在柯西(A.L.Cauchy)和魏尔斯特 w,的基础上去证明CH是否正确,没有人怀疑w1> 拉斯(K.Weierstrass)建立了严格的极限理论后,无 o的正确性.现在,在o1>o的基础上已经形成了 穷小量概念被抛弃,实无穷观被绝对地排斥,整个 许多自圆其说的“理论”,它们妨碍了后人对实无穷 19世纪几乎完全被潜无穷观统治2.直到19世纪 问题的继续探索.我们将直接证明①,>①,本身是 末康托尔创立集合论,才使实无穷规重新回到数学 不正确的,CH当然就不成立, 的视野,不过他建立的却是介乎潜无穷和实无穷之 笔者认为,所谓建立统一的实无穷概念就是要定 间的第3种无穷观,称为层次实无穷观(layered in- 义一个特殊的数∞,它在运算中必须满足2个条件: nity).为了与康托尔的实无穷观相区别,以后在称 1)0比任何有限数都大:2)不存在比如更大的数.康 他之前的实无穷规为统一实无穷观.概括起来看这 托尔规定正整数集的势为①,满足了对实无穷的条 3种无穷观的主张分别是: 件1),他用一一对应方法来确定2个无穷集之间的 1)潜无穷观:认为无穷是一个永无终止的增长 等势关系,已成功地证明对任意正整数n∈N,,n+ 过程,它不是数,不能参加运算,也就是说无穷只是 o=n×,=()”=w,成立.只是由于没有找到 一种说话方式,它表示对任何一个整数,都能找到一 证明2=o的合适方法,才最后放弃了对统一实无 个比它更大的数,但决不可能穷举所有的整数. 穷概念的追求,转而提出了相对实无穷概念.我们根 2)统一实无穷观:认为无穷是一个惟一存在的 据无穷编码的不变性(infinite coding invariance,ICI 特殊数,它不仅比任何有限数都大,而且不存在比无 原理)进一步证明2=w,说明⊙,能够满足实无穷 穷更大的数.也就是说无穷的任何运算结果都不会 的条件2),所以o,就是统一的实无穷∞,又由于∞ 大于无穷,无穷是能够包容一切增长过程的极限, 比任何有限数都大,其中已经包含了潜无穷的思想, 3)层次实无穷观:层次无穷观是现行的无穷 所以∞也是统一的无穷概念 观,它认为实无穷有不同的层次,最低的实无穷是可 数无穷oo,由于有性质n∈N,,n+oo=n×o0= 1 研究背景 (⊙,)”=0的保证,①,是一个相对稳定的特殊数; 1.1数的发展简史 更高一级的实无穷是不可数无穷①1,2=①1,其他 人类认识数至少已有30万年的历史,到19世 以此类推.这就像原子的能级结构一样,电子平常稳 纪实数概念已基本形成,其间经历了自然数、分数、 定在一个较低的能级上旋转,只有吸收到足够的能 数字“0”、负数和无理数等5个主要认识阶段,近 量后,才会上升到更高的能级.可见,在层次无穷观 100多年来对数的深入认识主要表现在2个方面: 中使用的是相对实无穷概念,而在实无穷观中使用 一是继续探索实无穷概念,以最终完成对实数性质 的是统一实无穷概念 的认识;二是通过对实数的组合运用,形成更复杂的 这3种无穷观都承认无穷是一个永无终止的增长 数,如复数(加入虚数)、狭义数(加入超复数)和广 过程,差别仅仅是无穷是否是数以及有多少个无穷. 义数(加入向量、张量、矩阵等)[31. 本文的论证目标是利用①的相对稳定性(即 1.23种无穷观 n∈N+,n+o0=nXo=(w)”=o)来直接证 在历史上关于无穷曾经出现过2种完全不同的 明2=①。成立,即证明更高一级的无穷0,根本不 观念:一种是潜无穷观(potential infinity),它认为无 存在,统一实无穷观是惟一正确的无穷观.为此首先 穷是一个永无终止的增长过程,它不是数;另一种是 介绍康托尔的层次实无穷观,并且分析他的成功和 实无穷观(actual infinity),它认为无穷是一个有确 不足 定含义的特殊数.亚里士多德(Aristotle)是历史上明 1.3可数集和不可数集 确区分实无穷和潜无穷的第一人,他的老师柏拉图 为了说明相对实无穷概念,康托尔把正整数集 (Plato)则是持实无穷观的最早代表.伽利略(G. N,定义为可数集(denumerable set)的基准,规定 Galilei)最先发现一个无穷集可与自己的真子集等 N,的势是最小的无穷①o·然后用一一对应方法来 势,他用一一对应的方法证明了自然数集{0,1,2, 确定一个无穷集A是否与N,等势(equinumerous), 3,4,…与平方数集{0,1,4,9,16,…等势,从 如果等势则A也可数;否则A不可数(uncountable)

·204 智能系统学报 第5卷 具有比N,更大的势.他已经成功地证明了整数 推论1可数集与有限集的并集是可数集;反 N,×N、有理数和代数数都可数.还证明了单位区 之,可数集可分解为一个有限集和可数集的并集. 间实数集和实数集等势,这反映在下面的一些重要 推论22个不同可数集的并集是可数集;反 定理中山,45] 之,可数集可分解为2个不同可数集的并集。 本文直接使用了朴素集合论中的许多基本概 推论3至多可数个不同可数集的并集是可数 念,如:“具有某种特定性质的事物的全体称之为集 集;反之,可数集可分解为至多可数个不同可数集的 合,组成集合的每一个事物称为该集合的元素”、 并集 “不含元素的集合称为空集”、“集合中的元素必 推论4对于任何n∈N+,可数集的势w具有 须具有确定性、互异性和无序性”、集合S中元素的 以下运算性质:n+o=n×=(oo)”=o 个数叫S的基数(cardinal number)或势(cardinali- 1.4实数不可数定理和连续统假设 y),用IS1表示. 在自然数的运算中,加法是最小的基本增值运 定义1如能在2个集合A、B的元素之间建立 算,其次是乘法和乘方,最大的基本增值运算是幂 对应关系,则称这2个集合等势,用1A1=|B1 乘.康托尔已经证明n+o=n×o=(o)”=, 表示 只要他能够进一步证明2=①0,统一实无穷的概 定义2如果1个集合能够和它的真子集等 念就成立了.遗憾的是由于康托尔始终没有找到证 势,则叫无穷集,否则叫有限集 明实数可数的一一对应方法,而在1874年得出了实 定义3正整数集N,={1,2,3,4,…是可 数不可数、20=o,>o0的结论,并根据这个结论在 数集,它的势是最小的实无穷,用超限基数⊙。表示. 1878年提出了连续统假设和层次无穷观.1874年康 由于有限集不能和自己的真子集等势,所以有 托尔证明实数不可数定理的过程十分复杂,对角论 限集之间等势关系的确定与元素之间的对应方式无 法是他3年后提出的另一个比较简单的证法[6.该 关.而无穷集可与自己的真子集等势,所以必须有如 方法用反证法证明单位区间的实数集R,是不可数 下定义4. 集合,下面用二进制数模仿康托尔的对角线法来进 定义4只要能找到1种方法证明无穷集A与 行实数不可数定理的证明(见图1) 正整数集N,等势,则称A为可数集;反之,只有所 RN 2 3 4 有的方法都不能证明A与N,等势时,才能称A为 X 0. a14 不可数集,不可数集的势大于可数集的势 0.aa a34 au 康托尔根据上述定义已经证明了下述结论: 0.a1 0.a4t A2 定理1单位区间实数集R,和任意有限区间 实数集R等势. 0.d4 定理2单位区间实数集R,和无限区间实数 集R等势。 定理3单位区间实数集R和正整数集N,的 0.6,bbb,…b,… 幂集p(N,)等势. 图1康托尔的对角线法 定理4自然数集N={0,1,2,3,4,…是可数集 Fig.1 Cantor's diagonal method 定理5正整数集N,的直积N,×N,是可数集, 伪定理1(实数不可数定理)单位区间实数集 定理6整数集Z={…,-4,-3,-2,-1,0, R1是不可数集,2=o1>o 1,2,3,4,…}是可数集, 证明用反证法证: 定理7奇数集0={…,-7,-5,-3,-1, 1)设R,是可数集,它必然与正整数集N,= 1,3,5,7,…}是可数集. {1,2,3,4,…,i,…}等势,可表示成R1={1,为, 定理8偶数集E={…,-8,-6,-4,-2, 3,x4,…,x,…},二者在i和(i=1,2,3,4,…之 0,2,4,6,8,…}是可数集, 间存在一一对应关系; 定理9有理数集Q={x|x=p/q,p,9∈Z, 2)将每一个单位区间实数都以无穷小数的全 q≠0,P,9间没有公因子}是可数集. 码形式x:=0.aaaadaa,4…a…表达,即保留二进制 定理10代数数集A={x|x是整系数代数方 编码中全部无效位和有效位,且不允许有近似性的 程的根}是可数集。 舍入出现(例如严格区分0.011…1和0.1000是2

第3期 何华灿,等:无穷概念的重新统一 ·205· 个完全不同的数): 1级保级函数无(o1)=n+o1=0+01=1, 3)规定实数集{x1,x2,x3,x4,…,,…}中的顺 f方(o1)=n×01=ww1=01和f方(01)=(⊙1)”= 序是随机排列的; ®,;用类似的方法还可证明这3个保级函数能推广 4)将每个x:=0.aa2aaa4…am…中am的值改 到任意级.由伪定理1知,康托尔已经发现的升级 变为{0,1}中的另一个值b: 函数只有g(ω:)=2=ω+1 5)这样就可得到单位区间中的一个新实数y= 由此可见,康托尔提出的相对实无穷不是统一 0.b,b2b3b4…b:…,由于y中至少有b:与x中的a 实无穷,因为它不是惟一存在的特殊数;但也不是潜 不相同,所以y生{1,x2,3,4,“,x,…; 无穷,因为它是特殊的数,有相对确定的大小,在各 6)由于x1,出2,x3,x4,…,龙,…的顺序是随机排 种保级函数的保护下具有相对的稳定性,只有在遇 列的,可以任意改变,a:的值也是随机出现的,可以 到升级函数作用时,才会改变它的大小.所以康托尔 任意改变,所以上述几,点已经一般性地证明了实数 的无穷观是层次实无穷观,他使用的是相对实无穷 集R,是可数集合的前提假设不成立: 概念.下面给出严格的数学描述, 7)根据定义4,实数集R1是不可数集合,其势 定义6如果存在一个超限基数∞,它对任意 IRI>0o; 正整数neN,满足:l)n00成立 ,①1,2,…(0+1=2,i=0,1,2,…),其中的任意 根据伪定理1(后面将用伪定理2证明它的错 o都满足:n∈N+,1)n<ω:;2)存在保级函数f(ω:)= 误),康托尔认为潜无穷观和统一实无穷观都不正 0:(如n+=n×==ω);3)存在升级函数 确,他提出了著名的连续统假设和超限基数假设,形 g(ω:)=2=0+1,则称ω:为相对实无穷 成了他自己的层次实无穷观. 假设1(连续统假设CH)在o,和w,之间没 概括起来说,康托尔的层次实无穷观有以下要点: 1)不存在一个统一的实无穷∞; 有其他的超限基数存在。 假设2(超限基数假设)实无穷不是一个惟一 2)存在无穷多个大小不同的相对实无穷o: 确定的特殊数,而是一个可无限增大的超限基数序 (①:+1=2,i=0,1,2,…); 列:00,01,02,(0+1=2,i=0,1,2,3,…). 3)正整数集的势是最小实无穷w,的典型代 康托尔曾经多次声称要给出连续统假设的证 表,单位区间实数集R的势是⊙1的典型代表,R 明,但直到临终他也没有发表.与他当年在数学界遭 幂集的势是o2的典型代表; 到普遍反对的情况不同,在现代数学中,康托尔的层 4)在每级无穷i内,都有一些保级函数f(ω:)= 次实无穷观和相对实无穷概念已经牢牢地占据了统 ®:使相对实无穷⊙:在i级内保持稳定不变; 治地位 5)只有升级函数g(ω:)=2=ω:+1才能提升相 1.5康托尔的层次实无穷观和相对实无穷概念 对实无穷的层次, 根据超限基数假设,康托尔把无穷分成了许多 形成康托尔层次实无穷观的关键因素是实数不 不同的等级:0级实无穷是可数无穷,它广泛存在, 可数定理(伪定理1),它是升级函数g(ω:)=2= 其典型实例是正整数集和有理数集的势;1级实无 ①:+1成立的理论依据,是促使实无穷不断升分级的 穷是不可数无穷,其典型实例是实数集和正整数幂 根源。要想建立统一实无穷理论,必须首先推翻这个 集的势;2级实无穷的典型实例是所有函数的集合 定理。 和R,幂集的势:2级以上的实例现在也说不清楚. 100多年来有不少数学家和哲学家发现,连续 定义5设f(w:)、g(o:)是定义在超限基数序 统假设为数学带来悖论和许多麻烦,因而怀疑康托 列0(i=0,1,2,3,…)上的基本增值函数,如果 尔的层次实无穷观,但至今没有找到解决它的有效 f(ω:)=①,则称f(ω:)为i级保级函数;如果 办法.在我国,一直有人在以各种不同的方式论证实 g(:)=@:+1,则称g(o:)为升级函数 数可数、连续统假设不成立,但是这些工作一直没有 由推论4知,康托尔已经证明在可数集合中有 引起数学界的足够重视781 0级保级函数f(w,)=n+o,=,f方(o,)=n× 本文将用无穷编码的不变性原理证明2”=成 00=⊙和f方(o,)=(⊙)”=⊙0;在不可数集合中有 立,重新统一无穷概念,所以下面直接用如表示无穷

·206 智能系统学报 第5卷 完全编码算法和自然数集 示平面中2条平行线能够在无穷远处相交,在直线 2 上增加一个无穷远点,得到了“扩充直线”的概 2.1自然数集的原始形态 念.又如在拓扑学中的单点紧化、非欧几何模型和数 1)最典型的无穷集是数集,而数集又有自然 论中的库默理想数等, 数、整数、有理数、实数、复数、狭义数和广义数之 5)自然数中的所有数都可用进位制数来具体 分3.从数的发展史上看,最早出现的是自然数, 表示(本文以二进制数为例进行讨论),从编码的角 它是纯粹的数字编码符号串.后来出现的各种数集 度看,尽管通常见到的有限数可以用有限位编码来 都是在这个编码符号串的基础上,或者在串外增加 表示,但理论上存在的无穷数必然是无穷位编码.所 小数点的位置标志,或者在串内增加某些辅助符号 以,为了得到数集中的全部数值,必须用无穷位计数 (如表示+、-的符号位,表示虚部和实部的i/r 器来生成这些数的编码.对有限数来说,编码中包含 位),或者给编码符号串指定位置标志(如在数组、 有效位和无效位,通常的表示方法是省略无效位,保 行列式中表示不同分量的特别标志符a),如此等 留有效位.而理论上存在的无穷数必须是无穷位编 等,就形成了不同类型的数集,所以从本质上看,各 码,其中没有无效位可以省略.为了方便讨论,规定 种数集都是变形的数字编码符号串,或者说是在自 一律使用无穷位全码表示法,不允许省略无效位. 然数编码基础上的变形. 综上几点,可以得出这样的结论:1)任何一个 2)本文讨论的各种无穷数集都是完全集,它包 完全的数集都需要用一个无穷位计数器来进行编 含了该数集中可能有的全部元素(数值),其中包括 码,编出的不同符号串代表数集中的不同数值;2) 通常见到的有限值数和理论上存在的无穷值数两大 数集中的数包括有穷值和无穷值,它们全都用无穷 部分,且可以从小到大顺序地排列. 位的编码符号串来表示,即本文中不允许把有穷值 3)自然数集同时具有内蕴性(inner implication 中的无效位省略. property)和排序性(ordering property)2种不同的性 不加任何辅助符号的数字编码符号串的直接解 质,它在无穷性方面也有2种不同的表现.内蕴性是 释就是自然数,所以称自然数集为原始数集,自然数 潜藏于自然数列中的微观属性,表现为个别数与数 集以外的其他数集为现实数集.本节用完全编码算 之间的各种不同关系,这些关系将随自然数列的不 法先研究原始形态的自然数集,下节再用完全译码 断延伸而变化,永远不可能被完全认识.排序性是自 算法研究各种添加了辅助符号的现实数集。 然数列中的宏观本性,表现为自然数列整体所具有 由康托尔的层次实无穷观知,尽管统一实无穷 的单一序结构,它不随自然数列的不断延伸而变化, 不存在,存在的都是相对实无穷,但以正整数集N 可以被完全认识.根据自然数集的内蕴性,必然主张 的势为代表的0级实无穷仍然是一个相对稳定的特 潜无穷观,认为无穷是一个永远不会完成的开放过 殊基数∞,∞的包容性已经非常强大,按照康托尔发 程,根据自然数集的排序性,可以形成实无穷观,认 现的0级保级函数知,n+9=n×=(o)”=o, 为无穷是一个已经完成了的封闭过程.可见康托尔 这就是说,的容量已经大到可以容下(∞)”多个 定义正整数集的势是实无穷∞,利用的就是自然数 ∞在里面,只是在遇见了升级函数2”后,才会升到 集的排序性,在这里正整数集{1,2,3,4,…}是一个 1级实无穷.本文将进一步证明∞不仅是相对稳定 已经完成了(延伸达于终止)的无限过程] 的特殊基数,而且是绝对稳定的特殊基数.也就是 4)由于{1,2,3,4,…{是一个已经完成了的无 说,先假定∞是0级实无穷,然后证明1级实无穷等 限过程,它有∞个元素,所以可用外推法在原来考虑 于0级实无穷,即是统一实无穷. 的对象{1,2,3,4,…}中添加理想元0而得到{1,2, 2.2完全编码算法 3,4,…,∞,这个新的数学实体既可把“∞”圈在其 根据图灵机原理,完全编码算法(complete en- 中,又把原来的东西原封不动地保留下来「4.{1,2, coding algorithm,CEA)由完全计数器(complete 3,4,…,∞的意思是集合中的元素可以无限制的 counter,CC)和原始存储器(primitive memory,PM) 增加,但是它总是从1开始,到∞结束.“无穷集合 两部分组成.CC的功能是按照二进制进行连续地计 在形式上有下界和上界”并不是荒谬的事情,例如 数,生成所有∞位二进制原始码,它从∞位0(用0… [0,1]区间的实数集就是这样,它从0开始,到1结 00表示)开始,不断地加1,直到∞位1(用1…11表 束,中间包含有无穷多个元素,其实,添加理想元素 示)结束,共生成了2”个不同的原始码.无穷位计数 的方法在数学中经常使用,如在射影空间中为了表 过程在理论上能够结束,是因为按照0级无穷的性

第3期 何华灿,等:无穷概念的重新统 ·207 质,理论上讲∞位是计数器的最高位,如果到位 {0,1,10,11,100,…,1…11},所以P的数值解释是 1…11后还要继续加1,将产生进位溢出,重新回到 自然数集N,按照定理4,P是可数集, ∞位0O0状态.PM的功能是顺序存放CC生成的 以后常常称原始码集合P={0…00,0…01, 所有原始码,它共有2”个存储单元,按照0,1,2, 0…010,0…011,…,1…11}为自然数集的原始形式 …,2-1顺序编号. 或者自然数集,称CC为自然数生成器,称PM为自 图2是PM的存储状态图,其中a1,a2,a,a4, 然数存储器 …,am表示计数器的o位,d,d1,d2,d3,…表示存储 推论5(无穷编码的不变性ICI原理)由∞位 器的地址编号.图2(a)是2位计数的状态,它共有 计数器生成的代码数仍然是0,即2”=0. 22=4种不同的原始编码:00、01、10、11;图2(b)是 在这里利用康托尔的相对实无穷概念和性质, 3位计数的状态,它共有2=8种不同的原始编码: 进一步证明了升级函数g(ω:)=2=⊙+1不成立, 000、001、010、011、100、101、110、111;图2(c)是∞ 相对实无穷o,就是惟一存在的实无穷∞. 位计数的状态,它共有2个不同的原始编码: 2.4ICI原理的物理解释 0…00,001,0…010,0011,…,1…11 ICI原理有3层含义,它们都体现在图2中,图 11d 11 d 2是一个值得反复领悟的重要对象, 10 10 d 第1层意思是关于∞是0级相对实无穷的诠 01 d 01 d 00 1☐00 d 释.由于0级保级函数的性质n+o=n×o= a:a ………… (∞)”=∞保持了0的相对稳定性,它最多可以容 (a) ……, 4 下(0)”多个∞而不会升级;所以在图2(c)中,无 0 1 论计数器CC的长度是相对地增加或是缩短,它仍 0 d 0 1 0 d 0 4+0 01 d 然是∞位.计数器CC的长度∞不变,它在PM中生 0 0 00 d 成的全部编码也就不变,仍然是从∞位0…00开始, 0 d 0 0 1 0 10 d 0 0 10d2 不断地加1,直到∞位1…11结束,这个计数状态图 001 d 0 001 d 十分稳定 000d 0 …000d a;dz a a a3 a:a 第2层意思是关于∞是统一实无穷的诠释.从 (b) (c) 图2(a)和(b)看,n位计数器可编出2"个码,显然有 图2PM的存储状态图 2">n,但是从图2(c)看,情况就完全不同了.尽管 Fig.2 Illustration of the storage states of PM ∞位计数器编出的码有2”个,但由于∞位计数器本 2.3ICI原理 身是自然数生成器,它编出的全部编码集就是自然 定理11原始码集合P={0…00,0…01, 数集,其势必然是0,所以2”=0,这就是说,用0 0…010,0…011,…,1…11}的势是2。 位的计数器,生成的全部编码集仍然是∞.所以有一 证明用数学归纳法证明如下(参见图2): 个无穷符号就完全够用了,不需要更多的无穷符 因为计数器的每一位都有0、1两种可能性,所 号,0是统一实无穷, 以由完全编码算法CEA可知,CC(2)可生成22=4 第3层意思是关于∞中有潜无穷思想的诠释. 个不同的原始码;CC(3)可生成2=8个不同的原 在实无穷的概念中并没有排斥潜无穷的思想,而是 始码;如果CC(n)可生成2”个不同的原始码,则 融进了潜无穷的思想.从图2(©)看,尽管计数器有 CC(n+1)可生成2×2”=2+'个不同的原始码;由 ∞位(即),但这个∞只是代表一个永无终止的 数学归纳法可知,当n→∞时,CC可生成2”个不同 增长过程的抽象符号.图2(c)用这个抽象符号规定 的原始码.而PM正好能够存放CC生成的2个不 了一个新的计数过程(即ω1),它从∞位0…00开 同的原始码,所以原始码集合P={0…00,0…01, 始,不断地加1,直到∞位1…11结束.由于这个计数 0…010,0…011,…,1…11}的势是2°. 过程要等待一个永无终止的增长过程,即全1…11 定理12原始码集合P={0…00,0…01, 状态的到来才能结束,所以这个计数过程也是一个 0010,0…011,…,1…11}的数值解释是自然数集 永无终止的增长过程,它仍然可以用同一个抽象符 N,P是可数集 号∞来代表.如果再把这个计数过程(即w,)当成 证明将P中的原始码看成是二进制整数,由 计数器的∞位,重新规定了一个新的计数过程(即 于其中的无效位并不影响数的值,得到的数值是 ①2),情况仍然会同样地重复下去,永远不会改变

·208. 智能系统学报 第5卷 (即o=w1=o2=…=∞).从这个意义上讲,在实 概括起来说,通过ICI原理可以得出如表1所 无穷∞中,包含有潜无穷的思想,即这个特殊数∞代 示的结论. 表的是一个永无终止的增长过程, 表1根据ICI原理所得出的结论 Table 1 The conclusions through the ICI principle 无穷观 被ICI原理证实的观点 被ICI原理证伪的观点 潜无穷观 无穷是一个永无终止的增长过程 无穷不是数,不能参加运算 无穷是一些特殊数,它比任何有限数都大(即它也是一个永无终止的增 因为20=0,>0,所以无穷 层次实无穷观长过程).具体体现在定义可数无穷①,=IN,I,用一一对应方法证明n 是一个不断增加的无穷序列 N,n+=n×o,=(o,)=o0 00,01,02,…(0+1=20,i= 0,1,2,3,…) 无穷是一个特殊数,它比任何有限数都大(即它也是一个永无终止的增 统一实无穷观长过程),不存在比无穷更大的数.具体体现在定义∞=1N,I,用一一对 无 应方法证明n∈N,n+∞=n×的=∞“=2“=o 现在已经很清楚,能够重新统一无穷概念的基 已经渗透到数学的每一个细胞,最近100多年来在 础是3种无穷观都认为无穷是一个永无终止的增长 它的基础上已经形成了各种各样自圆其说的概念、 过程.过去潜无穷论者之所以反对实无穷观,是因为 理论和学说,要想让人们马上接受这个颠覆性结果 他们没有发现用一个特殊的数(即理想元∞)来抽 绝非易事.可以想象,不少人的第一反应肯定是强烈 象地表示这个过程的方法:后来尽管康托尔发现了 的反对,他们会不自觉地根据在2”>0基础上形成 用一个特殊的数来抽象地表示这个过程的方法,但的这些概念、理论和学说,对2°=∞提出各种各样 由于没有找到证明2”=∞的有效方法,得出了 的疑问和非难,有的人甚至会不屑一顾,认为它不过 2”>∞的错误结论,所以他又提出层次实无穷观来 是众多的“民科抄作”之一.为了积极回应可能出现 反对统一实无穷观;本文在康托尔的基础上进一步 的疑问和非难,下面将用更多的方法来证明2”=∞ 证明了2”=,重新统一了无穷概念,最终确立了 成立,它们的作用和ICI原理等效. 统一实无穷观 1)利用单位区间实数集证明2”=0. ICI原理是信息世界的基本属性之一,这个性 定理13单位区间实数集R,与自然数集等 质对人类正确认识和理解与无穷有关的各种自然规 势,2°=0. 律有重要意义.ICI原理是理解本文的关键,而数的 证明单位区间实数集R,用无穷位小数的全 无穷位编码原理又是理解ICI原理的关键,它们是 码{0.0…00,0.0…001,0.0…010,0.0…011, 统一无穷概念、进一步建立统一实无穷理论的重要 0.00100,…,0.1…11{来表示,由于每位都有0、1 基础. 两种可能性,其势是2.又因为计数器的编码状态 2.5连续统假设不成立的更多证明 与小数点的有无毫无关系,显然在单位区间实数集 本来,ICI原理的发现已经直接推翻了2”>∞ 的全码与自然数集的全码之间存在如下的一一对应 的错误结论,层次无穷观已经失去了它存在的前提, 关系 自然就回到了统一实无穷观.但是,由于层次无穷观 白然数 0…000…010…0100…0110…0100…1…1山 单位区间实数0.0…000.0…010.0…0100.0…0110.0…0100…0.1…11 按照定义4知,单位区间实数集R,与自然数集 N,的每个子集中都有出现或不出现2种可能性,所 等势,IR|=0,所以,2”=0, 以p(N,)|=2°.将原始码集P中的0、1代码作下 2)利用正整数的幂集证明2”=, 列变换:将全部0变换成0,将a(i=1,2,3,4,…, 定理14正整数的幂集p(N)={0,{1}, ∞)位中的全部1变换成i,然后把每个∞位编码 {2},12,1,{3},…,{∞,…,4,3,2,1}}与自然数 串内部的符号取并集,就可以发现在正整数幂集 集等势,2”=0, p(N,)和原始码集P之间有如下的一一对应关系 证明由于N,的势是∞,而N,中每个元素在 存在
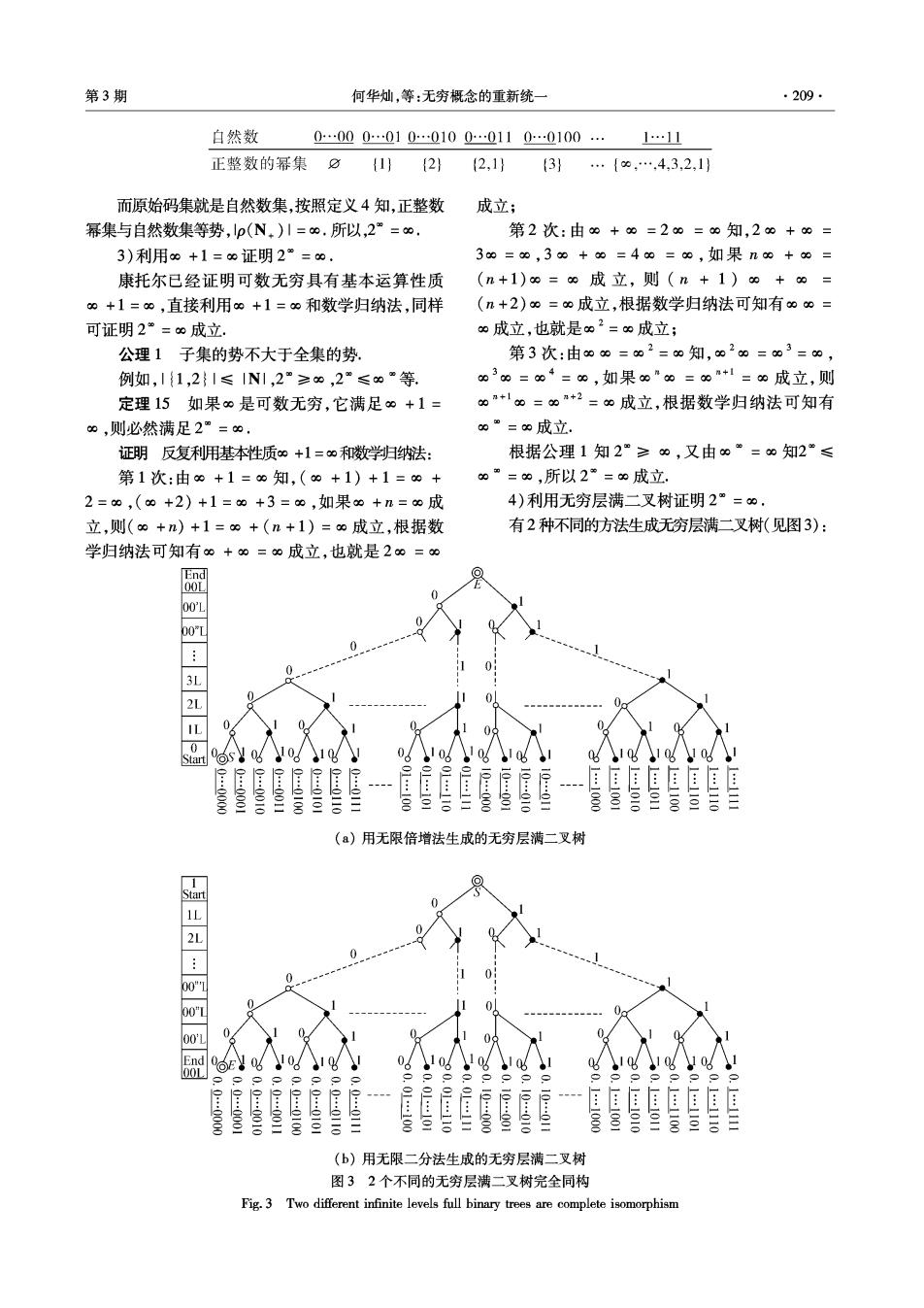
第3期 何华灿,等:无穷概念的重新统一 ·209· 白然数 0000…010…0100…0110…0100… 1…11 正整数的幂集 0 1} {2} 2.1} (3) …{,…4,3,2,1 而原始码集就是自然数集,按照定义4知,正整数 成立; 幂集与自然数集等势,p(N)1=o.所以,2°=o. 第2次:由0+0=20=∞知,20+o= 3)利用0+1=0证明2=0. 30=∞,30+的=4∞=0,如果n0+0= 康托尔已经证明可数无穷具有基本运算性质 (n+1)=o成立,则(n+1)o+o= 0+1=0,直接利用0+1=0和数学归纳法,同样 (n+2)0=0成立,根据数学归纳法可知有0co三 可证明2”=∞成立. 0成立,也就是02=0成立; 公理1子集的势不大于全集的势, 第3次:由00=02=0知,020=03=0, 例如,I{1,2}I≤1N|,2≥0,2≤∞"等. ∞3∞=∞4=0,如果0"9=0"+1=0成立,则 定理15如果是可数无穷,它满足0+1= 0n+10=0+2=0成立,根据数学归纳法可知有 0,则必然满足2”=∞. ∞。=9成立. 证明反复利用基本性质0+1=∞和数学归纳法: 根据公理1知2≥0,又由0=∞知2”≤ 第1次:由∞+1=0知,(0+1)+1=∞+ ∞”=的,所以2”=∞成立. 2=0,(0+2)+1=0+3=60,如果0+n=0成 4)利用无穷层满二叉树证明2”=∞. 立,则(0+n)+1=9+(n+1)=o成立,根据数 有2种不同的方法生成无穷层满二叉树(见图3): 学归纳法可知有0+0=∞成立,也就是2o=∞ 00L bo"L 3L ,0 art 0 106 (a)用无限倍增法生成的无穷层满二叉树 :0 0 00L 0 06 0.0.:0000 :二 三 9.::二0 .二 :00 :1010 1011 (b)用无限二分法生成的无穷层满二叉树 图3 2个不同的无穷层满二叉树完全同构 Fig.3 Two different infinite levels full binary trees are complete isomorphism

210 智能系统学报 第5卷 a)一种是自下向上的无限倍增法(见图3 最左叶结点0代表过程结束,用E表示.整个 (a)),它能够生成全部的自然数,其具体过程是: 无穷层满二叉树有层,2”个叶结点,每个叶结点 从最左叶结点S开始,它代表自然数0: 正好代表1个单位区间实数. 通过倍增生成第1层父结点,得到的叶结点代 对比图3(a)和(b)2棵无穷层满二叉树,尽管 表[0,1]中的全部自然数0和1; 一个代表自然数集,其势是©,另外一个代表单位区 通过倍增生成第2层父结点,得到的叶结点代 间实数,其势是2”;但它们都有∞层,2”个叶结点, 表[0,3]中的全部自然数0、1、10、11; 是完全同构的,而已经定义自然数集的势是∞,所以 通过倍增生成第3层父结点,得到的叶结点代 必然有2”=∞成立, 表[0,7]中的全部自然数0、1、10、11、100、101、110、 从康托尔的层次实无穷观到无穷概念的重新统 111; 一,历史走过了一个多世纪,但从公式上看,只差一 4 个符号:是2=0还是2”>∞?由于本文证明了 一般地,通过倍增生成第层父结点,得到的叶 2”=∞成立,升级函数变成了保级函数,促使实无 结点代表[0,2”-1]中的全部自然数0,1,10,11, 穷不断升级的根源消除了,层次实无穷观失去了理 100,101,110,111,…,1…11; 论支撑,自然回归为统一实无穷观。 2.6康托尔失误的原因 最后,通过倍增生成第∞层父结点,得到的叶结 康托尔证明实数不可数定理的基本思想是:正 点代表全部自然数0,1,10,11,100,101,110,111, 整数的势是∞,实数的势是2”,它们之间当然不可 …,1…11000,1…11001,1…11010,1…11011, 能建立一一对应关系.康托尔在对角线法中把单位 1…11100,1…11101,1…11110,1…11: 区间的实数表示成无穷位编码x:=0.aa2aa…a 根结点E表示过程结束.整个无穷层满二叉树 …a。,把正整数表示为几何点1,2,3,…,0,这没 有共有∞层,2°个叶结点。 有错误,因为任何一个数值点只有惟一一个数值编 b)另一种是自上向下的无限二分法(见图3(b), 码,反之亦然,错误发生在他把作为“点”的正整数 它能生成全部的单位区间实数,其具体过程是: 和无穷位编码形式的实数中“位”进行了一一对应 从根结点S开始,它代表将被分割的实数1; 的捆绑.这就使得问题的性质发生了根本的改变,不 用二分法生成根的第1层子结点0、1,它们代 再是数集和数集之间的比较,而成了在无穷位计数 表小数点后面1位的全部单位区间实数0.0、0.1; 器中,位数和它生成的编码数的直接比较.这就像是 用二分法生成根的第2层子结点00、01、10、 用计数器的“位数”作为长度单位,去丈量计数器生 11,它们代表小数点后面2位的全部单位区间实数 成的编码数目,结果肯定是2”/0不等于1(见图4 0.00、0.01、0.10、0.11: (a)).所以通过这样的捆绑后,用对角线法永远只 用二分法生成根的第3层子结点000、001、 能考察到实数中的一个真子集,没有可能遍及所有 010、011、100、101、110、111,它们代表小数点后面3 2°个不同的值.由定义4可知,根据对角线法只能 位的全部单位区间实数0.000、0.001、0.010、 得出在实数中存在许多可数的真子集的结论,不能 0.011、0.100、0.101、0.1100.111: 得出实数不可数的结论. 反之,如果承认对角线法的证明是正确的,那么 一般地,用二分法生成根的第n层子结点 同样可以利用它证明自然数集不可数.办法十分简 0…00,0…01,0…010,0…011,…,1…11,它们代表 单:只需在证明中将x:的小数点去掉,就得到一个 小数点后面n位的全部单位区间实数0.000, 全码表示的自然数x:=aa2aa…a…am.在这里x: 0.0-01,0.0…010,0.0-011,…,0.1…11 的表示与通常的自然数表示有2点不同:一般的表 示是从低位向高位排序为am…a#…a3a2a1,且有 最后,用无限二分法生成根的第∞层子结点 效位前面的0全部被省略.但这种形式上的差别不 0…00,0001,0…010,0011,…,1…11,它们代表 会影响证明的有效性.同样利用a:(i=1,2,3,…) 小数点后面位的全部单位区间实数0.0…00, 将自然数的位数和正整数的值数捆绑起来,就可以 0.0…001,0.0010,0.0011,…,0.1…11; 构造出一个新的自然数b=b,b2b3…bb。来,于是

第3期 何华灿,等:无穷概念的重新统 .211· 就证明了自然数集不可数!这和定理4是矛盾的. 详细的证明过程如下: 伪定理2(自然数不可数定理) 自然数集N 是不可数集,IN|=o 证明用反证法: (a)rv=nv=2- 1)假设N是可数集,它必然与正整数集N+= {1,2,3,4…,i,…}等势,可表示成N={1,x2,3, 4,…,x,…},在i和(i=1,2,3,4,…)之间存在 一一对应关系; (b)y=noo 2)将每一个自然数都以无穷位的全码形式x:= 图4实数集和自然数集都有0位和2“个值 dadzdad;4…at…表达,即保留有穷数的二进制编码 Fig.4 The number of digits are oo,and the number of 中全部无效位和有效位,不允许省略有效位前面的 values are 2,for real number set and the natu- 所有0(例如自然数“0”是无穷位全0(00…00),自 ral number set 然数“1”是无穷位全0后面一个1(0001)); 上述2次使用对角线法进行证明之所以都是错 3)规定自然数集{1,x2,3,x4,…,,…}中的 误的,其根本原因是:放在位数d位置上的正整数 顺序是随机排列的; 1,2,3,4,…保持着几何点的形式,而放在值数v位 4)将每个自然数无:=a1a2aga4…ai…中a的 置上的实数(或自然数)1,2,3,4,…被展开成了 值改变为{0,1}中的另一个值b:; 无穷位编码符号串x:=0.a1a2a3…a#…am(或者 5)这样就可得到一个新的全码形式的自然数 x:=aa2a3…aa…am,i=1,2,3,…,o),它们之间 y=bb2b3b4…b:…,由于y中至少有b:与x:中的aa 的一一对应关系是不同“质”的对应关系,没有可比 不相同,所以y{x1,x2,3,x4,…,,…}; 性,其结论当然是无效的.考察康托尔的其他证明, 6)由于自然数集{1,2,,4,…,x,…}的顺序 之所以都正确无误,是因为他把所有的数都同时作 是随机排列的,可以任意改变,a:的值也是随机出现 为几何点来看待的,是在同“质”的基础上进行的对 的,可以任意改变,所以上述几点已经一般性地证明了 比,也没有出现如图4(b)那样的整体和局部对应的 自然数集N是可数集合的前提假设不成立, 错误 7)根据定义4,自然数集N是不可数集合,其势 现在回头来分析,康托尔当年选择实无穷理论 INI>0o; 作为他的探索目标是正确的:他以集合论为工具来 8)由于自然数x=a1a2a3a4…am…中每位都 研究无穷概念的基本路线是正确的:他用元素之间 有O0、1两种取值的可能性,自然数集N的势INI= 的一一对应方法来判定集合间的等势关系也是正确 2,所以有20=ω1>w0成立. 的:他已经成功地证明了3个保级函数n+o=n× 这显然是个不可接受的错误证明,然而它与伪 0=(0)”=∞的成立,如果再进一步证明了2”= 定理1的证明过程完全一样,差别只是一个小数点 ∞也是保级函数,他建立实无穷的道路就全部打通 的有无!可见对角线法是否正确是值得怀疑的.更 了.但是由于“实数不可数定理”的失误,他得到了 有甚者,利用对角线法可以导出如下悖论:如果定义 一个使实无穷不断扩大的升级函数2”>∞,才不得 正整数集是可数集,则可以证明正整数集是不可数 不提出层次实无穷观和相对实无穷概念.可见康托 集.为什么会这样?从编码的角度看,其中的道理十 尔离建立实无穷概念的目标只差一步之遥,他没能 分简单,因为自然数集和实数的原始编码完全一样, 走完这最后一步是非常遗憾的,为此数学在这里徘 都有∞位和2”个不同的值,即rd=nd,w=nv(见图 徊了130多年! 4).而正整数集和自然数集两者只差一个自然数 3 完全译码算法和现实数 “0”,也有∞位和2”个不同的值.可见对角线法和 伪定理1都是错误的,康托尔的连续统假设、超限基 根据完全编码算法,已经从原理上明白了一个 数假设和层次实无穷观都是错误的. 重要的自然规律:无穷位计数器生成的全部编码仍 然是无穷个,也就是说通过无穷位计数器的编码不