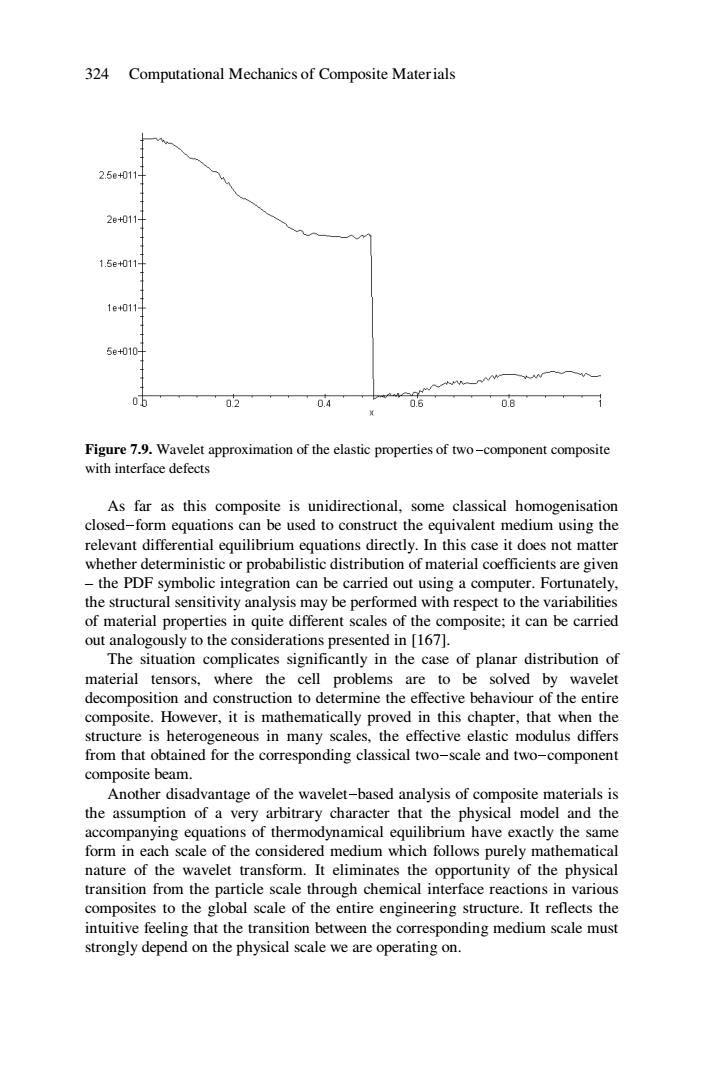
324 Computational Mechanics of Composite Materials 2.5e+011 2e+011 1.5e+011 1e011 5e+010H 05 02 0.4 0.6 0.8 Figure 7.9.Wavelet approximation of the elastic properties of two-component composite with interface defects As far as this composite is unidirectional,some classical homogenisation closed-form equations can be used to construct the equivalent medium using the relevant differential equilibrium equations directly.In this case it does not matter whether deterministic or probabilistic distribution of material coefficients are given -the PDF symbolic integration can be carried out using a computer.Fortunately, the structural sensitivity analysis may be performed with respect to the variabilities of material properties in quite different scales of the composite;it can be carried out analogously to the considerations presented in [167]. The situation complicates significantly in the case of planar distribution of material tensors,where the cell problems are to be solved by wavelet decomposition and construction to determine the effective behaviour of the entire composite.However,it is mathematically proved in this chapter,that when the structure is heterogeneous in many scales,the effective elastic modulus differs from that obtained for the corresponding classical two-scale and two-component composite beam. Another disadvantage of the wavelet-based analysis of composite materials is the assumption of a very arbitrary character that the physical model and the accompanying equations of thermodynamical equilibrium have exactly the same form in each scale of the considered medium which follows purely mathematical nature of the wavelet transform.It eliminates the opportunity of the physical transition from the particle scale through chemical interface reactions in various composites to the global scale of the entire engineering structure.It reflects the intuitive feeling that the transition between the corresponding medium scale must strongly depend on the physical scale we are operating on.324 Computational Mechanics of Composite Materials Figure 7.9. Wavelet approximation of the elastic properties of two-component composite with interface defects As far as this composite is unidirectional, some classical homogenisation closed-form equations can be used to construct the equivalent medium using the relevant differential equilibrium equations directly. In this case it does not matter whether deterministic or probabilistic distribution of material coefficients are given – the PDF symbolic integration can be carried out using a computer. Fortunately, the structural sensitivity analysis may be performed with respect to the variabilities of material properties in quite different scales of the composite; it can be carried out analogously to the considerations presented in [167]. The situation complicates significantly in the case of planar distribution of material tensors, where the cell problems are to be solved by wavelet decomposition and construction to determine the effective behaviour of the entire composite. However, it is mathematically proved in this chapter, that when the structure is heterogeneous in many scales, the effective elastic modulus differs from that obtained for the corresponding classical two-scale and two-component composite beam. Another disadvantage of the wavelet-based analysis of composite materials is the assumption of a very arbitrary character that the physical model and the accompanying equations of thermodynamical equilibrium have exactly the same form in each scale of the considered medium which follows purely mathematical nature of the wavelet transform. It eliminates the opportunity of the physical transition from the particle scale through chemical interface reactions in various composites to the global scale of the entire engineering structure. It reflects the intuitive feeling that the transition between the corresponding medium scale must strongly depend on the physical scale we are operating on