
7 Multiresolutional Wavelet Analysis 7.1 Introduction Multiscale analysis based on wavelet analysis,being a very modern and extensively developed numerical technique in signal theory [147,148,380],even in probabilistic context [289],introduces the capability to analyse the composite systems with multiple geometrical scales,which is very realistic for most engineering composites (the scales of microdefects,interface,reinforcement and the entire structure).Nowadays,this technique is employed in porous materials modelling [104],general FEM and BEM solutions for boundary problems [119],in vibration analysis [235]as well as in crack detection and impact damages [293,331,343],for instance.Figure 7.1 below presents the MATLAB illustration of the signal that can be interpreted as the information about the variability of heterogeneous medium physical properties in time(and/or in space).It is seen how such a signal can be decomposed using discrete wavelet transforms on the partially homogeneous parameters on different levels [169,170].After such a decomposition,the traditional or wavelet-based discrete numerical methods can be applied for computational physical modelling Continuous Wavelet Transfonn I-D 国x☒ scr过eTrarefom.tt4c0e"比teks time ler家*b Figure 7.1.Discrete and continuous wavelet signal transform
7 Multiresolutional Wavelet Analysis 7.1 Introduction Multiscale analysis based on wavelet analysis, being a very modern and extensively developed numerical technique in signal theory [147,148,380], even in probabilistic context [289], introduces the capability to analyse the composite systems with multiple geometrical scales, which is very realistic for most engineering composites (the scales of microdefects, interface, reinforcement and the entire structure). Nowadays, this technique is employed in porous materials modelling [104], general FEM and BEM solutions for boundary problems [119], in vibration analysis [235] as well as in crack detection and impact damages [293,331,343], for instance. Figure 7.1 below presents the MATLAB illustration of the signal that can be interpreted as the information about the variability of heterogeneous medium physical properties in time (and/or in space). It is seen how such a signal can be decomposed using discrete wavelet transforms on the partially homogeneous parameters on different levels [169,170]. After such a decomposition, the traditional or wavelet-based discrete numerical methods can be applied for computational physical modelling. Figure 7.1. Discrete and continuous wavelet signal transform

318 Computational Mechanics of Composite Materials The homogenisation method is still the most efficient way of computational modelling of composite systems.Usually it is assumed that there exists some scale relation between composite components and the entire system-two scales are introduced that are related by a scale parameter being some small real value tending most frequently to 0.An essential disadvantage of all these techniques is the impossibility of sensitivity analysis of composite homogenised characteristics with respect to geometrical scales relations. Wavelet analysis became very popular in the area of composite materials modelling because of their multiscale and stochastic nature.The most interesting issue is composite global behaviour,which is more important than the multiphysical phenomena appearing at different levels of their complicated multiscale structure.That is why it is necessary to build an efficient mathematical and numerical multiresolutional algorithm to analyse composite materials and structures. As is known,two essentially different ways are proposed to achieve this goal. First,the composite can be analysed directly using the wavelet decomposition-based FEM approach where the multiresolutional analysis can recover the material properties of any component at practically any geometrical level.The method leads to an exponential increase of the total number of degrees of freedom in the model-each new decomposition level increases this number. Alternatively,a multiscale homogenisation algorithm can be applied to determine effective material parameters of the entire composite and next,to carry out the classical FEM or other related method-based computations.The basic difference between these two approaches is that the wavelet decomposition and construction algorithms are incorporated into the matrix FEM computations in the first method.The second method is based on the determination of the effective material parameters and Finite Element analysis of the equivalent homogeneous system,where the dimensions of the original heterogeneous and homogenised problems are almost the same.An analogous two methodologies had been known before the wavelet analysis was incorporated in engineering computations. However the homogenisation method assumptions dealing with the interrelations between macro-and microscales were essentially less realistic. Considering the above,the aim of this chapter is to demonstrate the use of the wavelet-based homogenisation method in comparison with its preceding classical formulations.Effective material parameters of a periodic composite beam are determined symbolically in MAPLE and next,the temporal and spatial variability of thermal responses of homogenised systems are determined numerically and compared with the real structure behaviour.It is assumed here that material properties are temperature-independent,which should be extended next to the thermal-dependent behaviour.As is verified by the computational experiments,all homogenisation methods (classical and multiresolutional)give a satisfactory approximation of real heat transfer phenomena in the multiscale heterogeneous structure.The approach should be verified next for other types of composites as well as various physical and structural problems in both a deterministic and stochastic context.Separate studies should be carried out for the computer
318 Computational Mechanics of Composite Materials The homogenisation method is still the most efficient way of computational modelling of composite systems. Usually it is assumed that there exists some scale relation between composite components and the entire system – two scales are introduced that are related by a scale parameter being some small real value tending most frequently to 0. An essential disadvantage of all these techniques is the impossibility of sensitivity analysis of composite homogenised characteristics with respect to geometrical scales relations. Wavelet analysis became very popular in the area of composite materials modelling because of their multiscale and stochastic nature. The most interesting issue is composite global behaviour, which is more important than the multiphysical phenomena appearing at different levels of their complicated multiscale structure. That is why it is necessary to build an efficient mathematical and numerical multiresolutional algorithm to analyse composite materials and structures. As is known, two essentially different ways are proposed to achieve this goal. First, the composite can be analysed directly using the wavelet decomposition-based FEM approach where the multiresolutional analysis can recover the material properties of any component at practically any geometrical level. The method leads to an exponential increase of the total number of degrees of freedom in the model – each new decomposition level increases this number. Alternatively, a multiscale homogenisation algorithm can be applied to determine effective material parameters of the entire composite and next, to carry out the classical FEM or other related method-based computations. The basic difference between these two approaches is that the wavelet decomposition and construction algorithms are incorporated into the matrix FEM computations in the first method. The second method is based on the determination of the effective material parameters and Finite Element analysis of the equivalent homogeneous system, where the dimensions of the original heterogeneous and homogenised problems are almost the same. An analogous two methodologies had been known before the wavelet analysis was incorporated in engineering computations. However the homogenisation method assumptions dealing with the interrelations between macro- and microscales were essentially less realistic. Considering the above, the aim of this chapter is to demonstrate the use of the wavelet-based homogenisation method in comparison with its preceding classical formulations. Effective material parameters of a periodic composite beam are determined symbolically in MAPLE and next, the temporal and spatial variability of thermal responses of homogenised systems are determined numerically and compared with the real structure behaviour. It is assumed here that material properties are temperature–independent, which should be extended next to the thermal-dependent behaviour. As is verified by the computational experiments, all homogenisation methods (classical and multiresolutional) give a satisfactory approximation of real heat transfer phenomena in the multiscale heterogeneous structure. The approach should be verified next for other types of composites as well as various physical and structural problems in both a deterministic and stochastic context. Separate studies should be carried out for the computer

Multiresolutional Analysis 319 implementation of wavelet analysis in the Finite Element Method programs and comparison with the multiscale algorithm. Further,we demonstrate the application of the wavelet-based homogenisation method in comparison with its preceding classical formulation.Effective material parameters of the periodic composite beam are determined symbolically in MAPLE and next,the structural responses of the linear elastic homogenised systems are determined numerically and compared with the real structure vibrations.The eigenproblems for various combinations of the effective parameters are computed thanks to the specially adopted Finite Element Method computer code to determine the most efficient homogenisation method for the periodic multiscale composite.It is done for two-,three-and five-bay free supported periodic composite beams having their applications in the aerospace industry as well as in the modelling of bridge vibrations,for instance.As is verified by the computational experiments,the homogenisation methods (classical and multiresolutional)give a satisfactory approximation of the periodic composite beam eigenfrequencies.The approach should be verified next for other types of structures as well as for other structural problems in both deterministic and probabilistic context. Wavelet analysis is an especially promising tool in the domain of composite materials.It enables:(1)constructing the multiscale heterogeneous structures using particular wavelets which has to perfectly reflect the manufacturing process,for instance,and (2)multidimensional decomposition of the spatial distribution of composite materials and physical properties by the use of the wavelets of various types defined in different scales (heat conductivity or Young modulus along the heterogeneous specimen).The first opportunity corresponds to the analysis of experimental results (image analysis of composite morphology),while the second reflects the theoretical and computational analysis. Let us notice that the wavelet analysis introduces new meaning for the term composite.In the view of the analysis below we can distinguish homogeneous materials from composites using the following definition:the composite material and/or structure is such a heterogeneous continuum in which material or physical properties are related in macro-and microscales by at least a single wavelet transform.This definition extends traditional,rather engineering approach to composites where laminated or fibre-reinforced structures were considered (partially constant character of material characteristics)to those media with sinusoidal variability in one direction of these properties at least (see Figures 7.2-7.7 below).Figure 7.2 shows the spatial variability of the Young modulus using the following wavelet function [188]: The next figures present the contributions of various scales to the macroscale elastic characteristic of the entire composite structure
Multiresolutional Analysis 319 implementation of wavelet analysis in the Finite Element Method programs and comparison with the multiscale algorithm. Further, we demonstrate the application of the wavelet-based homogenisation method in comparison with its preceding classical formulation. Effective material parameters of the periodic composite beam are determined symbolically in MAPLE and next, the structural responses of the linear elastic homogenised systems are determined numerically and compared with the real structure vibrations. The eigenproblems for various combinations of the effective parameters are computed thanks to the specially adopted Finite Element Method computer code to determine the most efficient homogenisation method for the periodic multiscale composite. It is done for two-, three- and five-bay free supported periodic composite beams having their applications in the aerospace industry as well as in the modelling of bridge vibrations, for instance. As is verified by the computational experiments, the homogenisation methods (classical and multiresolutional) give a satisfactory approximation of the periodic composite beam eigenfrequencies. The approach should be verified next for other types of structures as well as for other structural problems in both deterministic and probabilistic context. Wavelet analysis is an especially promising tool in the domain of composite materials. It enables: (1) constructing the multiscale heterogeneous structures using particular wavelets which has to perfectly reflect the manufacturing process, for instance, and (2) multidimensional decomposition of the spatial distribution of composite materials and physical properties by the use of the wavelets of various types defined in different scales (heat conductivity or Young modulus along the heterogeneous specimen). The first opportunity corresponds to the analysis of experimental results (image analysis of composite morphology), while the second reflects the theoretical and computational analysis. Let us notice that the wavelet analysis introduces new meaning for the term composite. In the view of the analysis below we can distinguish homogeneous materials from composites using the following definition: the composite material and/or structure is such a heterogeneous continuum in which material or physical properties are related in macro- and microscales by at least a single wavelet transform. This definition extends traditional, rather engineering approach to composites where laminated or fibre-reinforced structures were considered (partially constant character of material characteristics) to those media with sinusoidal variability in one direction of these properties at least (see Figures 7.2-7.7 below). Figure 7.2 shows the spatial variability of the Young modulus using the following wavelet function [188]: ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ +⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ + ⎠ ⎞ ⎜ ⎝ ⎛ = + l x l x l x e x e 2 4 0 10 0.1sin 10 ( ) sin 0.1sin π π π , l=10. The next figures present the contributions of various scales to the macroscale elastic characteristic of the entire composite structure

320 Computational Mechanics of Composite Materials ereal 了可 20.5 20 19.5 19 2 6 10 Figure 7.2.Distribution of the Young modulus in the real composite e0 21+ 20.5 19.5 19 0 6 10 Figure 7.3.Zeroth order wavelet approximation of Young modulus in zeroth scale
320 Computational Mechanics of Composite Materials Figure 7.2. Distribution of the Young modulus in the real composite Figure 7.3. Zeroth order wavelet approximation of Young modulus in zeroth scale
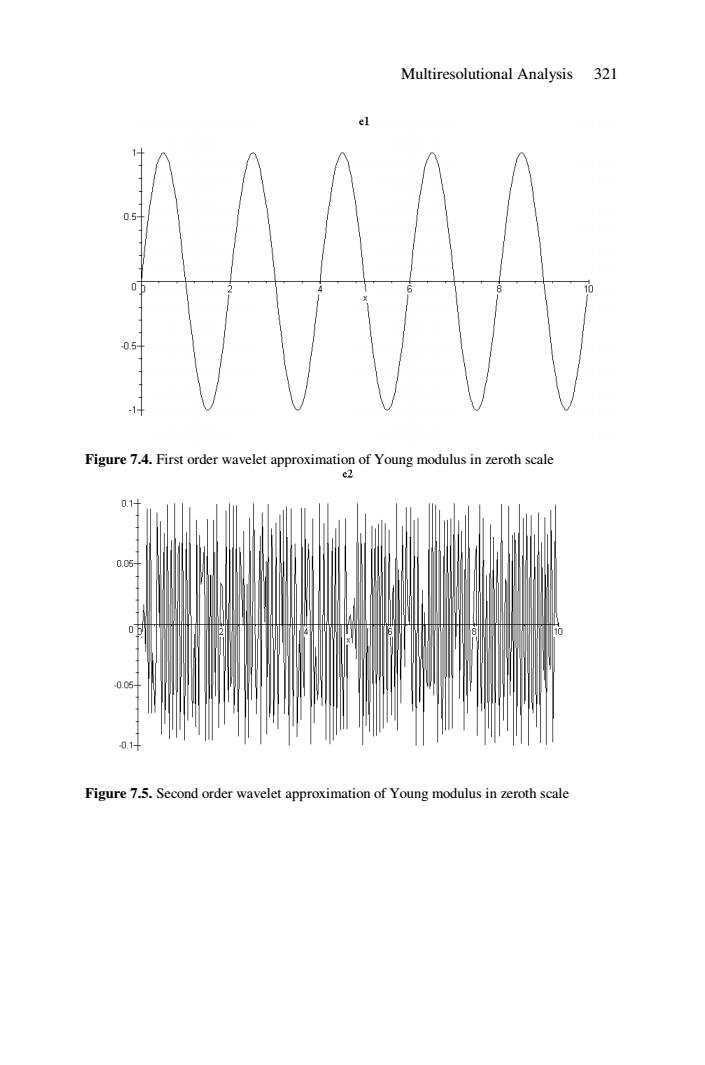
Multiresolutional Analysis 321 el 05 0 05 -1 Figure 7.4.First order wavelet approximation of Young modulus in zeroth scale e2 0.1 0.05 -0.05 -01+ Figure 7.5.Second order wavelet approximation of Young modulus in zeroth scale
Multiresolutional Analysis 321 Figure 7.4. First order wavelet approximation of Young modulus in zeroth scale Figure 7.5. Second order wavelet approximation of Young modulus in zeroth scale
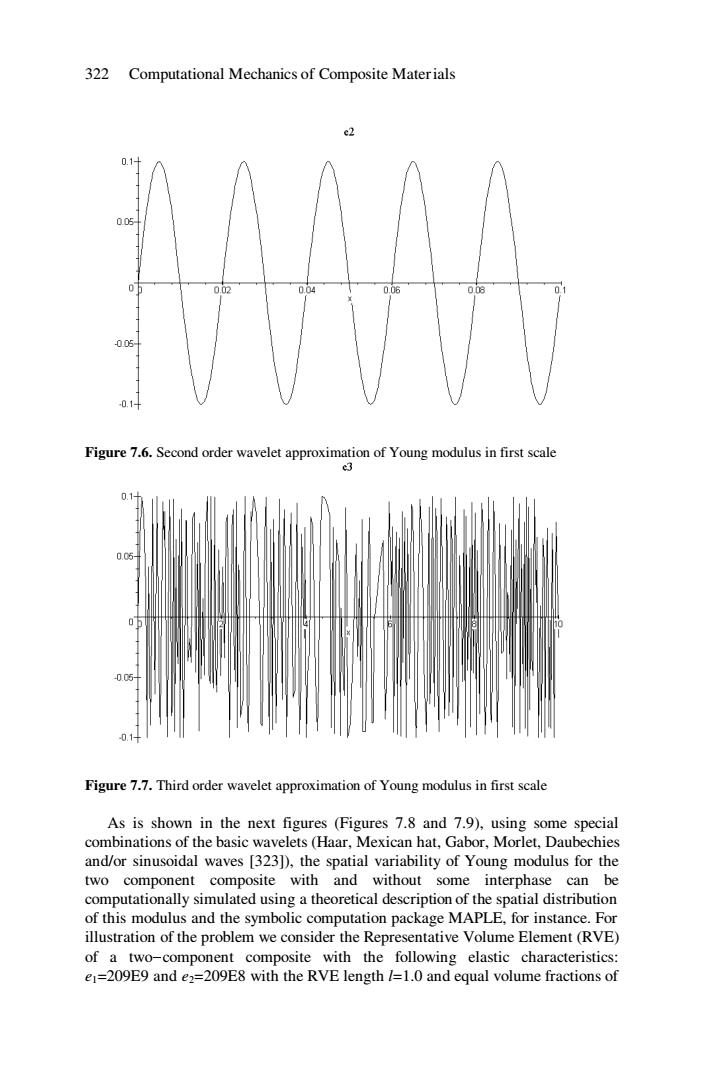
322 Computational Mechanics of Composite Materials e2 0.1+ 0.05 01 0.02 0.04 0.06 008 005 -0.1+ Figure 7.6.Second order wavelet approximation of Young modulus in first scale e3 0.1 0.0吃 0.05 -0.1 Figure 7.7.Third order wavelet approximation of Young modulus in first scale As is shown in the next figures (Figures 7.8 and 7.9),using some special combinations of the basic wavelets (Haar,Mexican hat,Gabor,Morlet,Daubechies and/or sinusoidal waves [323]),the spatial variability of Young modulus for the two component composite with and without some interphase can be computationally simulated using a theoretical description of the spatial distribution of this modulus and the symbolic computation package MAPLE,for instance.For illustration of the problem we consider the Representative Volume Element(RVE) of a two-component composite with the following elastic characteristics: e1=209E9 and e2=209E8 with the RVE length /=1.0 and equal volume fractions of
322 Computational Mechanics of Composite Materials Figure 7.6. Second order wavelet approximation of Young modulus in first scale Figure 7.7. Third order wavelet approximation of Young modulus in first scale As is shown in the next figures (Figures 7.8 and 7.9), using some special combinations of the basic wavelets (Haar, Mexican hat, Gabor, Morlet, Daubechies and/or sinusoidal waves [323]), the spatial variability of Young modulus for the two component composite with and without some interphase can be computationally simulated using a theoretical description of the spatial distribution of this modulus and the symbolic computation package MAPLE, for instance. For illustration of the problem we consider the Representative Volume Element (RVE) of a two-component composite with the following elastic characteristics: e1=209E9 and e2=209E8 with the RVE length l=1.0 and equal volume fractions of
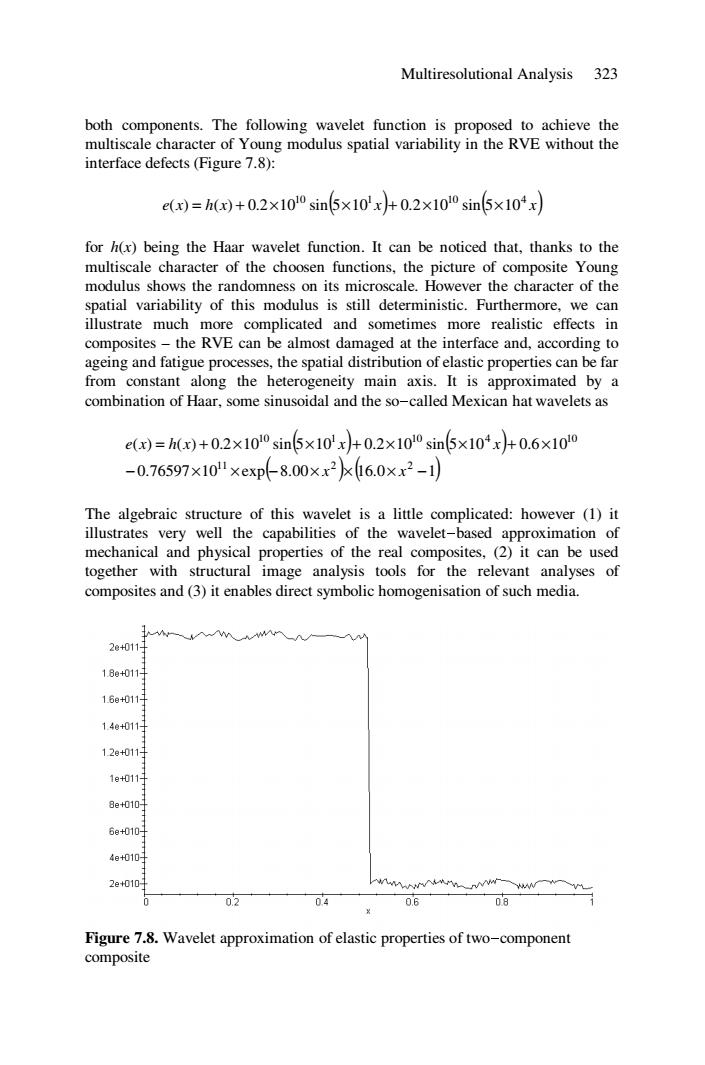
Multiresolutional Analysis 323 both components.The following wavelet function is proposed to achieve the multiscale character of Young modulus spatial variability in the RVE without the interface defects (Figure 7.8): e()=h(w)+0.2×100sin5×10'x+0.2x100sin5×104x for h(x)being the Haar wavelet function.It can be noticed that,thanks to the multiscale character of the choosen functions,the picture of composite Young modulus shows the randomness on its microscale.However the character of the spatial variability of this modulus is still deterministic.Furthermore,we can illustrate much more complicated and sometimes more realistic effects in composites-the RVE can be almost damaged at the interface and,according to ageing and fatigue processes,the spatial distribution of elastic properties can be far from constant along the heterogeneity main axis.It is approximated by a combination of Haar,some sinusoidal and the so-called Mexican hat wavelets as e()=h(x)+0.2×100sin5×10'x+0.2x10l0si5×104x+0.6×100 -0.76597×10l×exp8.00×x2kl6.0xx2-1 The algebraic structure of this wavelet is a little complicated:however (1)it illustrates very well the capabilities of the wavelet-based approximation of mechanical and physical properties of the real composites,(2)it can be used together with structural image analysis tools for the relevant analyses of composites and(3)it enables direct symbolic homogenisation of such media. 2e+011 18e+011- 16e+011 14e+011] 12g+011月 1g+011 8e+0101 6e+010- 4e+010月 2e+0101 0.2 04 0.6 5 Figure 7.8.Wavelet approximation of elastic properties of two-component composite
Multiresolutional Analysis 323 both components. The following wavelet function is proposed to achieve the multiscale character of Young modulus spatial variability in the RVE without the interface defects (Figure 7.8): e x h x ( x) ( x) 10 1 10 4 ( ) = ( ) + 0.2×10 sin 5×10 + 0.2×10 sin 5×10 for h(x) being the Haar wavelet function. It can be noticed that, thanks to the multiscale character of the choosen functions, the picture of composite Young modulus shows the randomness on its microscale. However the character of the spatial variability of this modulus is still deterministic. Furthermore, we can illustrate much more complicated and sometimes more realistic effects in composites – the RVE can be almost damaged at the interface and, according to ageing and fatigue processes, the spatial distribution of elastic properties can be far from constant along the heterogeneity main axis. It is approximated by a combination of Haar, some sinusoidal and the so-called Mexican hat wavelets as () ( ) 0.76597 10 exp( )( ) 8.00 16.0 1 ( ) ( ) 0.2 10 sin 5 10 0.2 10 sin 5 10 0.6 10 11 2 2 10 1 10 4 10 − × × − × × × − = + × × + × × + × x x e x h x x x The algebraic structure of this wavelet is a little complicated: however (1) it illustrates very well the capabilities of the wavelet-based approximation of mechanical and physical properties of the real composites, (2) it can be used together with structural image analysis tools for the relevant analyses of composites and (3) it enables direct symbolic homogenisation of such media. Figure 7.8. Wavelet approximation of elastic properties of two-component composite
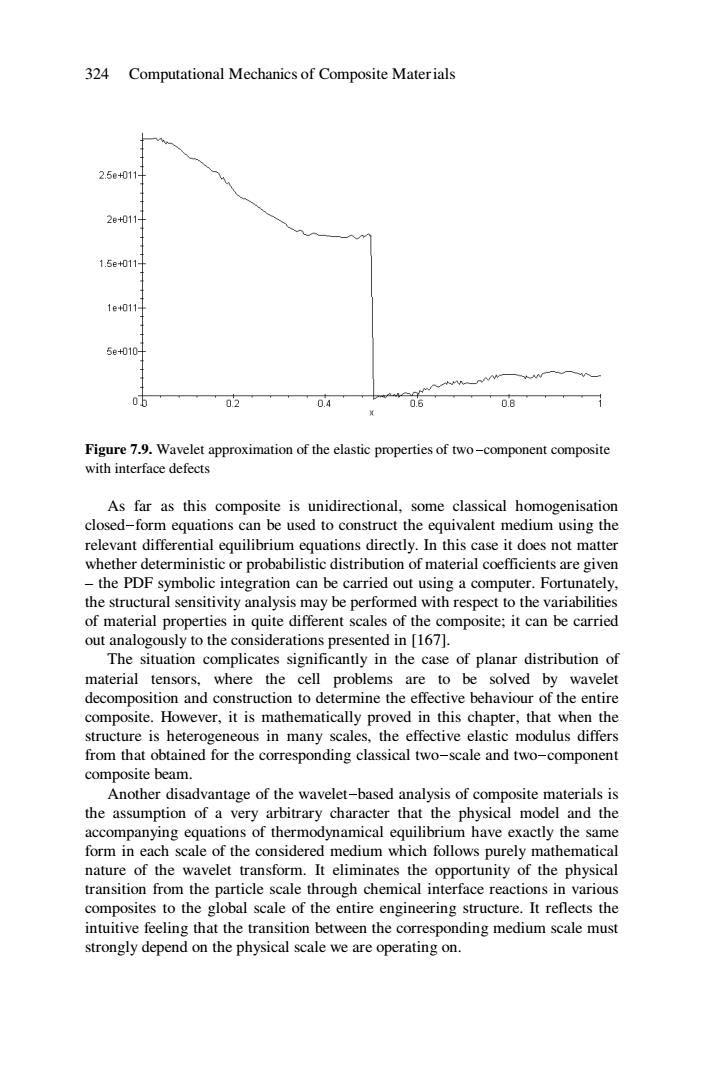
324 Computational Mechanics of Composite Materials 2.5e+011 2e+011 1.5e+011 1e011 5e+010H 05 02 0.4 0.6 0.8 Figure 7.9.Wavelet approximation of the elastic properties of two-component composite with interface defects As far as this composite is unidirectional,some classical homogenisation closed-form equations can be used to construct the equivalent medium using the relevant differential equilibrium equations directly.In this case it does not matter whether deterministic or probabilistic distribution of material coefficients are given -the PDF symbolic integration can be carried out using a computer.Fortunately, the structural sensitivity analysis may be performed with respect to the variabilities of material properties in quite different scales of the composite;it can be carried out analogously to the considerations presented in [167]. The situation complicates significantly in the case of planar distribution of material tensors,where the cell problems are to be solved by wavelet decomposition and construction to determine the effective behaviour of the entire composite.However,it is mathematically proved in this chapter,that when the structure is heterogeneous in many scales,the effective elastic modulus differs from that obtained for the corresponding classical two-scale and two-component composite beam. Another disadvantage of the wavelet-based analysis of composite materials is the assumption of a very arbitrary character that the physical model and the accompanying equations of thermodynamical equilibrium have exactly the same form in each scale of the considered medium which follows purely mathematical nature of the wavelet transform.It eliminates the opportunity of the physical transition from the particle scale through chemical interface reactions in various composites to the global scale of the entire engineering structure.It reflects the intuitive feeling that the transition between the corresponding medium scale must strongly depend on the physical scale we are operating on
324 Computational Mechanics of Composite Materials Figure 7.9. Wavelet approximation of the elastic properties of two-component composite with interface defects As far as this composite is unidirectional, some classical homogenisation closed-form equations can be used to construct the equivalent medium using the relevant differential equilibrium equations directly. In this case it does not matter whether deterministic or probabilistic distribution of material coefficients are given – the PDF symbolic integration can be carried out using a computer. Fortunately, the structural sensitivity analysis may be performed with respect to the variabilities of material properties in quite different scales of the composite; it can be carried out analogously to the considerations presented in [167]. The situation complicates significantly in the case of planar distribution of material tensors, where the cell problems are to be solved by wavelet decomposition and construction to determine the effective behaviour of the entire composite. However, it is mathematically proved in this chapter, that when the structure is heterogeneous in many scales, the effective elastic modulus differs from that obtained for the corresponding classical two-scale and two-component composite beam. Another disadvantage of the wavelet-based analysis of composite materials is the assumption of a very arbitrary character that the physical model and the accompanying equations of thermodynamical equilibrium have exactly the same form in each scale of the considered medium which follows purely mathematical nature of the wavelet transform. It eliminates the opportunity of the physical transition from the particle scale through chemical interface reactions in various composites to the global scale of the entire engineering structure. It reflects the intuitive feeling that the transition between the corresponding medium scale must strongly depend on the physical scale we are operating on

Multiresolutional Analysis 325 7.2 Multiscale Reduction and Homogenisation Therefore,a multiresolutional homogenisation method is proposed for numerical analysis together with various stochastic computational techniques, which makes it possible to determine probabilistic characteristics of various multiscale composites.Considering the fact that the multiresolutional method makes it possible to determine the effective physical characteristics in a closed form,the stochastic second order perturbation approach is applied to analyse the multiscale randomness of the entire composite in the most general form. Let us consider the following differential equilibrium equation to distinguish the differences between a classical asymptotic approach and multiresolutional scheme: =fx) x∈0,] (7.1) where e(x),defining material properties of the heterogeneous medium,varies arbitrarily on many scales (macro,meso and micro,etc.).The unit interval denotes here the Representative Volume Element(RVE),also called the periodicity cell. The classical result obtained through the asymptotic homogenisation theory is given by (2.71)for deterministic composites exhibiting two separate geometrical scales linked by the scale parameter e-this is the weakest point of this approach. Sometimes e is treated as a positive real number tending to 0(practically an infinite number of the RVEs in the composite)and,alternatively,some small positive parameter.As it can be demonstrated,the essential differences are observed in these two models.Now,this parameter is treated as some real functions introduced as the wavelet function relating two or more separate geometrical scales of the composite. In contrast to the classical approach to the homogenisation problem,the multiresolution approach uses the algebraic transformation between scales provided by the multiresolution analysis to solve for the fine-scale behaviour and explicitly eliminate it from the equation.This approach has the advantage that the coefficients may vary on arbitrarily many scales.The chain of subspaces ...cVCVCVCVCVC... (7.2) defines the hierarchy of scales that the multiresolution scheme uses.This chain of subspaces is defined in such a way that the space V is"finer"than the space V in the sense that (1)all of V is contained in V,,and(2)the component of V which is not in V consists of functions which resolve features on a scale finer than any function in V may resolve.The difference between successive spaces in this chain is captured by the so-called wavelet space W,defined to the
Multiresolutional Analysis 325 7.2 Multiscale Reduction and Homogenisation Therefore, a multiresolutional homogenisation method is proposed for numerical analysis together with various stochastic computational techniques, which makes it possible to determine probabilistic characteristics of various multiscale composites. Considering the fact that the multiresolutional method makes it possible to determine the effective physical characteristics in a closed form, the stochastic second order perturbation approach is applied to analyse the multiscale randomness of the entire composite in the most general form. Let us consider the following differential equilibrium equation to distinguish the differences between a classical asymptotic approach and multiresolutional scheme: ( ) u(x) f (x) dx d e x dx d ⎟ = ⎠ ⎞ ⎜ ⎝ ⎛ − ; ] x ∈[0,1 (7.1) where e(x), defining material properties of the heterogeneous medium, varies arbitrarily on many scales (macro, meso and micro, etc.). The unit interval denotes here the Representative Volume Element (RVE), also called the periodicity cell. The classical result obtained through the asymptotic homogenisation theory is given by (2.71) for deterministic composites exhibiting two separate geometrical scales linked by the scale parameter ε - this is the weakest point of this approach. Sometimes ε is treated as a positive real number tending to 0 (practically an infinite number of the RVEs in the composite) and, alternatively, some small positive parameter. As it can be demonstrated, the essential differences are observed in these two models. Now, this parameter is treated as some real functions introduced as the wavelet function relating two or more separate geometrical scales of the composite. In contrast to the classical approach to the homogenisation problem, the multiresolution approach uses the algebraic transformation between scales provided by the multiresolution analysis to solve for the fine-scale behaviour and explicitly eliminate it from the equation. This approach has the advantage that the coefficients may vary on arbitrarily many scales. The chain of subspaces ... ... ⊂ V2 ⊂V1 ⊂V0 ⊂ V−1 ⊂ V−2 ⊂ (7.2) defines the hierarchy of scales that the multiresolution scheme uses. This chain of subspaces is defined in such a way that the space Vj is “finer” than the space Vj+1 in the sense that (1) all of Vj+1 is contained in Vj , and (2) the component of Vj which is not in Vj+1 consists of functions which resolve features on a scale finer than any function in Vj+1 may resolve. The difference between successive spaces in this chain is captured by the so-called wavelet space Wj+1 , defined to the

326 Computational Mechanics of Composite Materials orthogonal complement of V in V,.An orthogonal basis for the wavelet space Wis constructed which has vanishing moments,i.e.the basis elements are L'-orthogonal to low-degree polynomials.The existence of orthogonal wavelet bases with vanishing moments distinguishes the multiresolution approach from typical multi-scale discretisations provided by finite-element or hierarchical bases.If we are considering a multiresolution analysis defined on a bounded domain,then the hierarchy of scales defined above has the coarsest scale (which is called V),and we write instead VocV1cV-2c.… (7.3) Let us review the multiresolution strategy for the reduction and homogenisation of linear problems.Let us consider to this purpose a bounded linear operator S,:VV,.Since V,is spanned by translations of the function x-k).we know that the operator S,may be written in the form of a matrix.If the multiresolution analysis is defined on a bounded domain,then this matrix is finite; otherwise it is an infinite matrix,which we consider as an operator on L2.Let us consider the equation Six=f (7.4) The decomposition V=VW allows us to split the operator S,into four pieces(recall that W is called the wavelet space and is the"detail"or fine-scale component of V,)and write 色)H) (7.5) where we have A,:W*→W Bg,:V#1→W (7.6) Cs,:Wn→VH T,:V#→V and dd,W.ss,V are the L2-orthogonal projections of x and fonto the W and V spaces.The projection s is thus the coarse-scale component of
326 Computational Mechanics of Composite Materials orthogonal complement of Vj+1 in Vj . An orthogonal basis for the wavelet space Wj+1 is constructed which has vanishing moments, i.e. the basis elements are 2 L -orthogonal to low-degree polynomials. The existence of orthogonal wavelet bases with vanishing moments distinguishes the multiresolution approach from typical multi-scale discretisations provided by finite-element or hierarchical bases. If we are considering a multiresolution analysis defined on a bounded domain, then the hierarchy of scales defined above has the coarsest scale (which is called V0 ), and we write instead ... V0 ⊂ V−1 ⊂ V−2 ⊂ (7.3) Let us review the multiresolution strategy for the reduction and homogenisation of linear problems. Let us consider to this purpose a bounded linear operator S j Vj →Vj : . Since Vj is spanned by translations of the function ( ) x k j φ 2 − , we know that the operator S j may be written in the form of a matrix. If the multiresolution analysis is defined on a bounded domain, then this matrix is finite; otherwise it is an infinite matrix, which we consider as an operator on 2 L . Let us consider the equation S x f j = (7.4) The decomposition Vj =Vj+1 ⊕Wj+1 allows us to split the operator S j into four pieces (recall that Wj+1 is called the wavelet space and is the “detail” or fine-scale component of Vj ) and write ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ =⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ f f x x S S S S s d s d C T A B j j j j (7.5) where we have 1 1 1 1 1 1 1 1 : : : : + + + + + + + + → → → → S j j S j j S j j S j j T V V C W V B V W A W W j j j j (7.6) and 1 , dx d y ∈Wj+ , 1 , x y ∈Vj+ s s are the 2 L -orthogonal projections of x and f onto the Wj+1 and Vj+1 spaces. The projection x s is thus the coarse-scale component of