
8 Appendix 8.1 Procedure of MCCEFF Input File Preparation The instructions described below deal with the preparing of input data file to the MCCEFF analysis in the case there is no need to use the mesh generator. 1.Heading line (12a4)general information 2.General information about the problem homogenised(6i5) Column Variable Description 1-5 NUMNP Total number of nodal point in the structure discretised 6-10 NELTYP Total number of finite element groups(=1) 11-15 LL Total number of load cases (=3) 36-40 KEQB Total number of non-zero degrees of freedom in the main matrix 66-70 MK Total number of random trials 71-75 NBN Total number of nodal points of the interfaces General comments: A.NELTYP variable is provided due to the original POLSAP code to extend in the next version the MCCEFF code with the analysis of the engineering structures homogenised (e.g.fibre-reinforced plates and shells).However due to its constant value it may have been omitted. B.LL variable is provided taking into account that in the next versions of the program the rest of the effective tensor components will be computed (in the 3D homogenisation problem).There are three different components of the elasticity tensor homogenised for the plane strain problems being solved by the program. C.KEQB parameter should be modified (default value is equal to 0)if the program MCCEFF in the process of main stiffness matrix formation or solution of the fundamental algebraic equations system stops running.The value of the parameter is to be taken from the interval [O,NEQB].where NEQB is the total number of the degrees of freedom of the composite cell.The probability of the successful computations increases with decreasing KEQB parameter
8 Appendix 8.1 Procedure of MCCEFF Input File Preparation The instructions described below deal with the preparing of input data file to the MCCEFF analysis in the case there is no need to use the mesh generator. 1. Heading line (12a4) general information 2. General information about the problem homogenised (6i5) Column Variable Description 1-5 NUMNP Total number of nodal point in the structure discretised 6-10 NELTYP Total number of finite element groups (=1) 11-15 LL Total number of load cases (=3) 36-40 KEQB Total number of non-zero degrees of freedom in the main matrix 66-70 MK Total number of random trials 71-75 NBN Total number of nodal points of the interfaces General comments: A. NELTYP variable is provided due to the original POLSAP code to extend in the next version the MCCEFF code with the analysis of the engineering structures homogenised (e.g. fibre-reinforced plates and shells). However due to its constant value it may have been omitted. B. LL variable is provided taking into account that in the next versions of the program the rest of the effective tensor components will be computed (in the 3D homogenisation problem). There are three different components of the elasticity tensor homogenised for the plane strain problems being solved by the program. C. KEQB parameter should be modified (default value is equal to 0) if the program MCCEFF in the process of main stiffness matrix formation or solution of the fundamental algebraic equations system stops running. The value of the parameter is to be taken from the interval [0,NEQB], where NEQB is the total number of the degrees of freedom of the composite cell. The probability of the successful computations increases with decreasing KEQB parameter

Appendix 383 3.Nodal points data (7i5,4d10.0,3i2) Column Variable Description 2-5 N Nodal point number 7-10 X(N,1) 11-15 XN,2) 16-20 XN,3) Displacement boundary conditions codes 21-25 XN,4) =0,free degree of freedom 26-30 N,5) =1,fixed degree of freedom 31-35 XN,6) 36-45 X(N) X coordinate 46-55 Y(N) Y coordinate 56-65 Z(N) Z coordinate 66-70 K(N) Nodal point generation code 71-72 MI Number of the internal region 73-74 M2 Number of the external region 75-77 M3 The interface end code (=1) General comments: A.Nodal point numbering has to be continuous and to start from number 1,which should denote the centre of the fibre (considering stress boundary conditions computations). B.Interface nodal points numbering has to be provided in the anticlockwise system and the distances between any two points must be equal. C.The structure being discretised should be placed in the YZ plane;the X coordinate will be used in the next version for the analysis of the 3D composite problems. D.The regions of the different materials should have increasing number starting from the central component (fibre in two-component composites)and continuous to the external boundary of the cell. E.In the case of half or quarter of the periodicity cell analysis the M3 parameter should be used to underline the ends of the interface being cutted. 4.General finite elements data (3i5) Column Variable Description 1-5 =3 Plane strain code 6-10 NUMEL Total number of finite elements 11-15 NUMMAT Total number of composite components
Appendix 383 3. Nodal points data (7i5,4d10.0,3i2) Column Variable Description 2-5 N Nodal point number 7-10 IX(N,1) 11-15 IX(N,2) 16-20 IX(N,3) Displacement boundary conditions codes 21-25 IX(N,4) =0, free degree of freedom 26-30 IX(N,5) =1, fixed degree of freedom 31-35 IX(N,6) 36-45 X(N) X coordinate 46-55 Y(N) Y coordinate 56-65 Z(N) Z coordinate 66-70 K(N) Nodal point generation code 71-72 M1 Number of the internal region 73-74 M2 Number of the external region 75-77 M3 The interface end code (=1) General comments: A. Nodal point numbering has to be continuous and to start from number 1, which should denote the centre of the fibre (considering stress boundary conditions computations). B. Interface nodal points numbering has to be provided in the anticlockwise system and the distances between any two points must be equal. C. The structure being discretised should be placed in the YZ plane; the X coordinate will be used in the next version for the analysis of the 3D composite problems. D. The regions of the different materials should have increasing number starting from the central component (fibre in two-component composites) and continuous to the external boundary of the cell. E. In the case of half or quarter of the periodicity cell analysis the M3 parameter should be used to underline the ends of the interface being cutted. 4. General finite elements data (3i5) Column Variable Description 1-5 =‘3’ Plane strain code 6-10 NUMEL Total number of finite elements 11-15 NUMMAT Total number of composite components
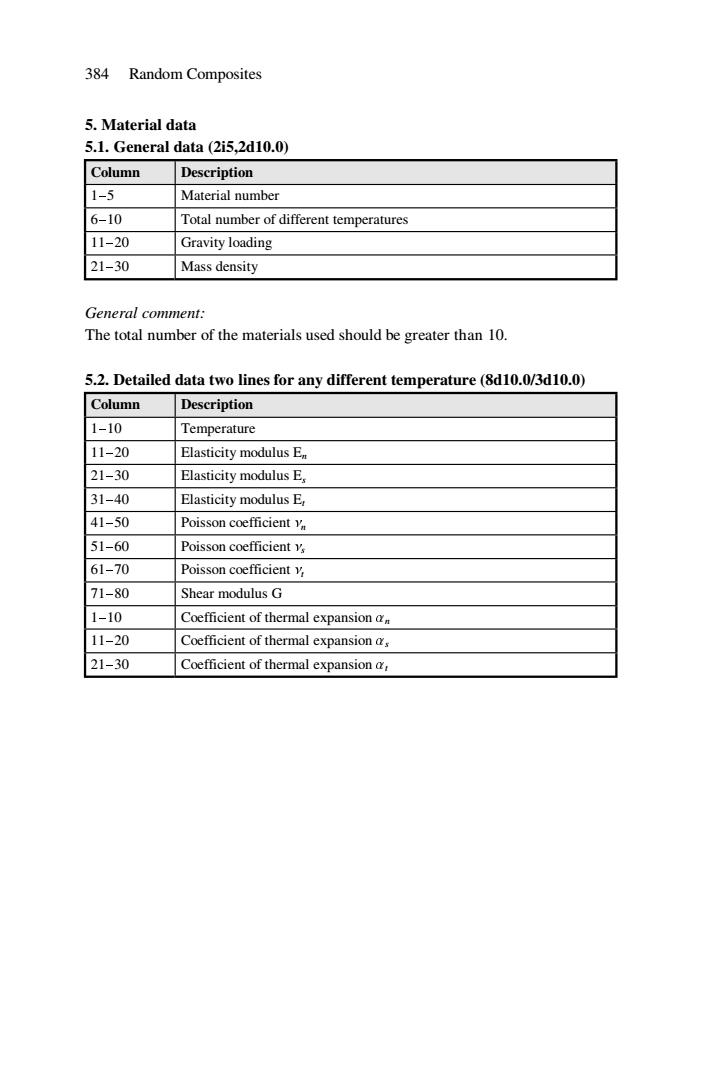
384 Random Composites 5.Material data 5.1.General data (2i5,2d10.0) Column Description 1-5 Material number 6-10 Total number of different temperatures 11-20 Gravity loading 21-30 Mass density General comment: The total number of the materials used should be greater than 10. 5.2.Detailed data two lines for any different temperature(8d10.0/3d10.0) Column Description 1-10 Temperature 11-20 Elasticity modulus E 21-30 Elasticity modulus E 31-40 Elasticity modulus E, 41-50 Poisson coefficient y 51-60 Poisson coefficient y, 61-70 Poisson coefficient y, 71-80 Shear modulus G 1-10 Coefficient of thermal expansion 11-20 Coefficient of thermal expansion a, 21-30 Coefficient of thermal expansion a
384 Random Composites 5. Material data 5.1. General data (2i5,2d10.0) Column Description 1-5 Material number 6-10 Total number of different temperatures 11-20 Gravity loading 21-30 Mass density General comment: The total number of the materials used should be greater than 10. 5.2. Detailed data two lines for any different temperature (8d10.0/3d10.0) Column Description 1-10 Temperature 11-20 Elasticity modulus En 21-30 Elasticity modulus Es 31-40 Elasticity modulus Et 41-50 Poisson coefficient nn 51-60 Poisson coefficient ns 61-70 Poisson coefficient nt 71-80 Shear modulus G 1-10 Coefficient of thermal expansion an 11-20 Coefficient of thermal expansion as 21-30 Coefficient of thermal expansion at
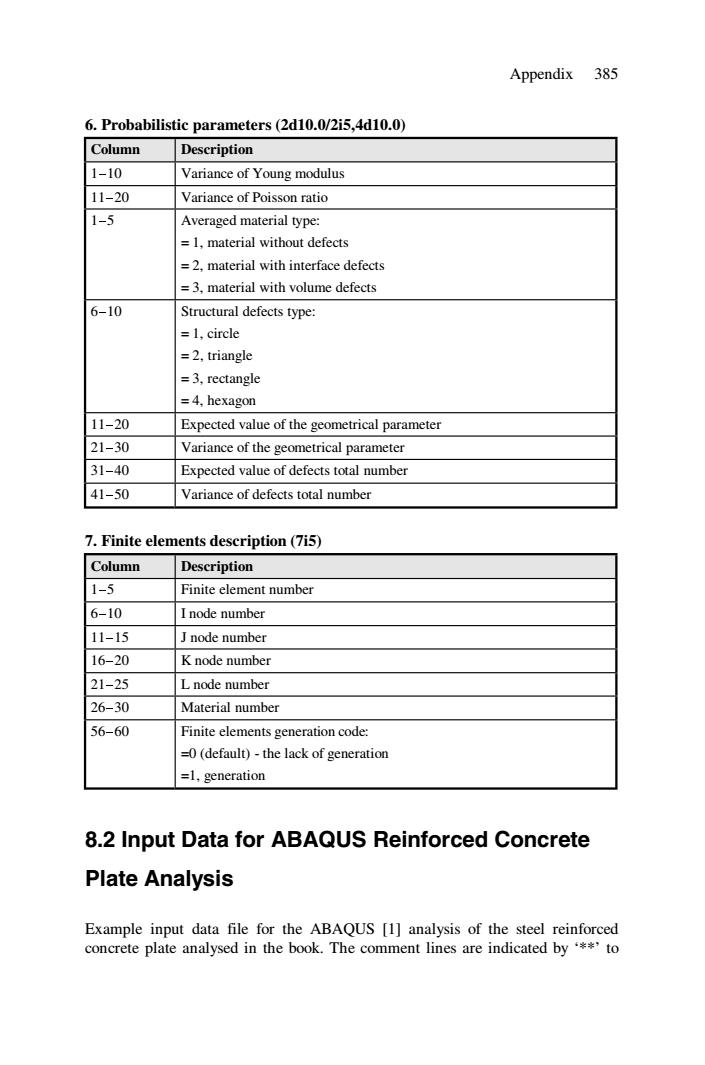
Appendix 385 6.Probabilistic parameters(2d10.0/2i5,4d10.0) Column Description 1-10 Variance of Young modulus 11-20 Variance of Poisson ratio 1-5 Averaged material type: =1,material without defects =2,material with interface defects =3,material with volume defects 6-10 Structural defects type: =1.circle =2,triangle =3,rectangle =4,hexagon 11-20 Expected value of the geometrical parameter 21-30 Variance of the geometrical parameter 31-40 Expected value of defects total number 41-50 Variance of defects total number 7.Finite elements description(7i5) Column Description 1-5 Finite element number 6-10 I node number 11-15 J node number 16-20 K node number 21-25 L node number 26-30 Material number 56-60 Finite elements generation code: =0(default)-the lack of generation =1,generation 8.2 Input Data for ABAQUS Reinforced Concrete Plate Analysis Example input data file for the ABAQUS [1]analysis of the steel reinforced concrete plate analysed in the book.The comment lines are indicated by '*to
Appendix 385 6. Probabilistic parameters (2d10.0/2i5,4d10.0) Column Description 1-10 Variance of Young modulus 11-20 Variance of Poisson ratio 1-5 Averaged material type: = 1, material without defects = 2, material with interface defects = 3, material with volume defects 6-10 Structural defects type: = 1, circle = 2, triangle = 3, rectangle = 4, hexagon 11-20 Expected value of the geometrical parameter 21-30 Variance of the geometrical parameter 31-40 Expected value of defects total number 41-50 Variance of defects total number 7. Finite elements description (7i5) Column Description 1-5 Finite element number 6-10 I node number 11-15 J node number 16-20 K node number 21-25 L node number 26-30 Material number 56-60 Finite elements generation code: =0 (default) - the lack of generation =1, generation 8.2 Input Data for ABAQUS Reinforced Concrete Plate Analysis Example input data file for the ABAQUS [1] analysis of the steel reinforced concrete plate analysed in the book. The comment lines are indicated by ‘**’ to

386 Random Composites enable the user to gain a better understanding of model computed.The lines indicated by*or without any indication are program execution lines. *heading corner supported shell **all material and geometrical parameters are defined in US units *node 1,0.0. 7,18.,0. 61.0.18. 67,18.,18. *node numbers,their coordinates *ngen,nset=y-sym 1,7 *node generation on the 'y-sym'boundary with numbers from I to 7 *ngen,nset=x-sym 1.61,10 *node generation on the 'x-sym'boundary with numbers from 1 to 61 with increment equal to 10 *ngen,nset=lx2 61,67 *node generation on the 'Ix2'boundary with numbers from 61 to 67 *ngen,nset=ly2 7.67,10 *nodes generation on the 'ly2'boundary with numbers from 7 to 67 with increment equal to 10 *nset,nset=one 1, **definition of the nodes set called 'one' *nfill x-sym,ly2,6,1 **generation ('filling')of the nodes contained in the internal of the rectangular given by parallel boundaries 'y-sym','x-sym','Ix2'and 'ly2' *element,type=s8r.elset=slab **element type and element set definition 1,13,23,21,2,13,22,11 **master element definition:corner and midpoint nodes in anti-clockwise order *elgen,elset=slab **element generation for the element set 'slab
386 Random Composites enable the user to gain a better understanding of model computed. The lines indicated by ‘*’ or without any indication are program execution lines. *heading corner supported shell **all material and geometrical parameters are defined in US units *node 1,0.,0. 7,18.,0. 61,0.,18. 67,18.,18. ** node numbers, their coordinates *ngen,nset=y-sym 1,7 ** node generation on the ‘y-sym’ boundary with numbers from 1 to 7 *ngen,nset=x-sym 1,61,10 ** node generation on the ‘x-sym’ boundary with numbers from 1 to 61 with increment equal to 10 *ngen,nset=lx2 61,67 ** node generation on the ‘lx2’ boundary with numbers from 61 to 67 *ngen,nset=ly2 7,67,10 ** nodes generation on the ‘ly2’ boundary with numbers from 7 to 67 with increment equal to 10 *nset,nset=one 1, **definition of the nodes set called ‘one’ *nfill x-sym,ly2,6,1 **generation (‘filling’) of the nodes contained in the internal of the rectangular given by parallel boundaries ‘y-sym’, ‘x-sym’, ‘lx2’ and ‘ly2’ *element,type=s8r,elset=slab **element type and element set definition 1,1,3,23,21,2,13,22,11 **master element definition: corner and midpoint nodes in anti-clockwise order *elgen,elset=slab **element generation for the element set ‘slab’

Appendix 387 1,3,2.1,320.3 **master element number,number of elements to be defined in the first **row generated including the master element,increment in node numbers **of corresponding nodes from element to element in row (default is 1). **increment in element numbers in row (default is 1),numbers of rows to **be defined(default is 1),increment in node numbers of corresponding **nodes from row to row,increment in element numbers of corresponding **elements from row to row,numbers of layers to be defined(defined is **1),increment in node numbers of corresponding nodes from layer to **layer,increment in element numbers of corresponding elements from **layer to layer *shell section,elset=slab,material=al 1.75.9 **shell thickness,total number of the integration points through its thickness *material,name=al **concrete material parameters definition *elastic 4.15e6,.15 **Young modulus,Poisson ratio *concrete 3000.,0. 5500..0015 **absolute value of compressive stress,absolute value of plastic strain (the **first stress-strain point must be at zero plastic strain and defines the **initial yield point) *failure ratios 1.16,.0836 **ratio of the ultimate biaxial compressive stress to the uniaxial **compressive ultimate stress(default is 1.16),absolute value of the ratio **of uniaxial tensile stress at failure to the uniaxial compressive stress at **failure(default is 0.09),the ratio of the magnitude of a principal **component of plastic strain at ultimate stress in biaxial compression to **the plastic strain at ultimate stress in uniaxial compression,the ratio of **the tensile principal stress value at cracking,in plane stress,when the **other non-zero principal stress component is at the ultimate compressive **stress value,to the tensile cracking stress under uniaxial tension. *tension stiffening **definition of retained tensile stress normal to a crack is a function of the **deformation in the direction of the normal to the crack
Appendix 387 1,3,2,1,3,20,3 **master element number, number of elements to be defined in the first **row generated including the master element, increment in node numbers **of corresponding nodes from element to element in row (default is 1), **increment in element numbers in row (default is 1), numbers of rows to **be defined (default is 1), increment in node numbers of corresponding **nodes from row to row, increment in element numbers of corresponding **elements from row to row, numbers of layers to be defined (defined is **1), increment in node numbers of corresponding nodes from layer to **layer, increment in element numbers of corresponding elements from **layer to layer *shell section,elset=slab,material=a1 1.75,9 **shell thickness, total number of the integration points through its thickness *material,name=a1 **concrete material parameters definition *elastic 4.15e6,.15 **Young modulus, Poisson ratio *concrete 3000.,0. 5500.,.0015 **absolute value of compressive stress, absolute value of plastic strain (the **first stress-strain point must be at zero plastic strain and defines the **initial yield point) *failure ratios 1.16 , .0836 **ratio of the ultimate biaxial compressive stress to the uniaxial **compressive ultimate stress (default is 1.16), absolute value of the ratio **of uniaxial tensile stress at failure to the uniaxial compressive stress at **failure (default is 0.09), the ratio of the magnitude of a principal **component of plastic strain at ultimate stress in biaxial compression to **the plastic strain at ultimate stress in uniaxial compression, the ratio of **the tensile principal stress value at cracking, in plane stress, when the **other non-zero principal stress component is at the ultimate compressive **stress value, to the tensile cracking stress under uniaxial tension. *tension stiffening **definition of retained tensile stress normal to a crack is a function of the **deformation in the direction of the normal to the crack

388 Random Composites 1.,0. 0.,2.e-3 **fraction of remaining stress to stress at cracking,absolute value of the **direct strain minus the direct strain at cracking *rebar,element=shell,material=slabmt,geometry=isoparametric,name=yy **definition of the rebars,reinforced element type,material name,rebar **geometry type (isoparametric or skew),name of the rebars group slab.014875,1.,-.435,4 **definition of rebars geometry,cross-sectional area of each rebar,spacing **of the rebars in the plane of the shell,position of the rebars in the shell **direction,edge number to which rebar are similar [4] *rebar,element=shell,material=slabmt,geometry=isoparametric,name=xx slab.014875,1.,-.435,1 material.name=slabmt *elastic 29.e6 **Young modulus,Poisson ratio is default *plastic 50.e3 **Yield stress value *boundary **displacement boundary condition definition y-sym,ysymm x-sym,xsymm **symmetry conditions on x-sym,y-sym boundaries 67,3 *restart,write,frequency=999 **option RESTART controls the writing to and reading of the restart file, **which is used by the postprocessor;the option will create a restart **file after each increment at which the increment number is exactly **divisible by N,and at the end of each step of the analysis,regardless of **the value of N at that time *step,inc=30 **option STEP must begin each step definition,parameter INC is equal to **the maximum number of increments in a step(upper bound,the default **value is 10) *static,riks **this option indicates that the step should be analysed as a static load **step:the Riks method is chosen by the RIKS parameter
388 Random Composites 1.,0. 0.,2.e-3 **fraction of remaining stress to stress at cracking, absolute value of the **direct strain minus the direct strain at cracking *rebar,element=shell,material=slabmt,geometry=isoparametric,name=yy **definition of the rebars, reinforced element type, material name, rebar **geometry type (isoparametric or skew), name of the rebars group slab,.014875,1.,-.435,4 **definition of rebars geometry, cross-sectional area of each rebar, spacing **of the rebars in the plane of the shell, position of the rebars in the shell **direction, edge number to which rebar are similar [4] *rebar,element=shell,material=slabmt,geometry=isoparametric,name=xx slab,.014875,1.,-.435,1 *material,name=slabmt *elastic 29.e6 **Young modulus, Poisson ratio is default *plastic 50.e3 **Yield stress value *boundary **displacement boundary condition definition y-sym,ysymm x-sym,xsymm **symmetry conditions on x-sym, y-sym boundaries 67,3 *restart,write,frequency=999 **option RESTART controls the writing to and reading of the restart file, **which is used by the postprocessor; the option will create a restart **file after each increment at which the increment number is exactly **divisible by N, and at the end of each step of the analysis, regardless of **the value of N at that time *step,inc=30 **option STEP must begin each step definition, parameter INC is equal to **the maximum number of increments in a step (upper bound, the default **value is 10) *static,riks **this option indicates that the step should be analysed as a static load **step; the Riks method is chosen by the RIKS parameter

Appendix 389 05,1,1,3,-1. **initial time increment,time period of the step,minimum time increment **allowed,maximum increment allowed,maximum value of the load **proportionality factor for the Riks method,node number at which the **value is being monitored,degree of freedom being monitored,value of **the total displacement (or rotation)at the node and degree of freedom **which,if crossed during an increment,ends the step at that increment *cload **concentrated loading definition 1,3,-5000. **node number,number of the corresponding degree of freedom,loading **magnitude in the orientation given by the user by ordering nodes into **shell elements *el print,frequency=10 **option provided tabular printed output of element variables;parameter **FREQUENCY is equal to the output frequency measured in the **increments performed(if this option is omitted,very large printed output **files will be produced by large models in multiple increment analysis!) **all stress components sinv **all stress invariants(MISES,TRESC,PRESS-equivalent pressure stress, **INV3-third stress invariant) c **all strain components pe *all plastic strain component crack **crack orientations in concrete *el file,frequency=10 sinv e pe crack *node file,nset=one **this option allows nodal variables to be written to the ABAQUS results **file (no nodal variables will be written to the results file unless this **option is used!)
Appendix 389 .05,1.,,,,1,3,-1. **initial time increment, time period of the step, minimum time increment **allowed, maximum increment allowed, maximum value of the load **proportionality factor for the Riks method, node number at which the **value is being monitored, degree of freedom being monitored, value of **the total displacement (or rotation) at the node and degree of freedom **which, if crossed during an increment, ends the step at that increment *cload **concentrated loading definition 1,3,-5000. **node number, number of the corresponding degree of freedom, loading **magnitude in the orientation given by the user by ordering nodes into **shell elements *el print,frequency=10 **option provided tabular printed output of element variables; parameter **FREQUENCY is equal to the output frequency measured in the **increments performed (if this option is omitted, very large printed output **files will be produced by large models in multiple increment analysis!) s **all stress components sinv **all stress invariants (MISES,TRESC,PRESS-equivalent pressure stress, **INV3-third stress invariant) e **all strain components pe ** all plastic strain component crack **crack orientations in concrete *el file,frequency=10 s sinv e pe crack *node file,nset=one **this option allows nodal variables to be written to the ABAQUS results **file (no nodal variables will be written to the results file unless this **option is used!)

390 Random Composites 《 *end step **FURTHER COMMENTS **it is possible to provide SHEAR RETENTION parameter to describe the **reduction of the shear modulus as a function of the tensile strain across the **crack;if this parameter is omitted(should be placed after TENSION **STIFFENING lines),it is assumed that the shear retention behaviour depends **only on temperature.EXPANSION parameter may be used to introduce thermal **volume change effects in the concrete.The NLGEOM parameter may be **included in the STEP option when the large strains and rotations associated with **failure of concrete are observed. 8.3 MAPLE Script for Computations of the Homogenised Heat Conductivity Coefficients Mexican hat-Haar basis plot of the input heat conductivity >restart;sig=-.5;k1=0.1;k2:=0.4; kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x 2/(2*sig 2)))(x 2/sig 2-1)); >khaar:=piecewise(x=0.5,k2); >k:=khaar+0.005*kmexh; plot(k,x=0..1,title='k'); Mexican hat-Haar basis heat conductivity contrast variability restart;sig:=-.5;k1:=contrast"k2;k2:=0.05; kmexh:=2+1/(sqrt(2*Pi)*sig 3)*((exp(-x 2/(2*sig 2)))*(x^2/sig 2-1)); >khaar:=piecewise(x=0.5,k2); >k:=khaar+0.005*kmexh; plot3d(k,x=0..1,contrast=5..100,title='k'); Spatial averaging of the Mexican hat-Haar type heat conducitivity >restart;sig:=-.5;k1=0.1;k2:=0.4; kmexh:=2+1/(sqrt(2*Pi)*sig 3)*((exp(-x2/(2*sig2)))*(x 2/sig 2-1)); khaar:=piecewise(x=0.5,k2); >k:=khaar+0.005*kmexh; >plot(k,x=0..1,title='k'); >kav:=evalf(int(k,x=0..1)); Classical homogenisation of the Mexican hat-Haar basis type heat conductivity >restart;sig=-.5;k1:=0.1;k2:=0.4;
390 Random Composites u *end step **FURTHER COMMENTS **it is possible to provide SHEAR RETENTION parameter to describe the **reduction of the shear modulus as a function of the tensile strain across the **crack; if this parameter is omitted (should be placed after TENSION **STIFFENING lines), it is assumed that the shear retention behaviour depends **only on temperature. EXPANSION parameter may be used to introduce thermal **volume change effects in the concrete. The NLGEOM parameter may be **included in the STEP option when the large strains and rotations associated with **failure of concrete are observed. 8.3 MAPLE Script for Computations of the Homogenised Heat Conductivity Coefficients Mexican hat - Haar basis plot of the input heat conductivity > restart; sig:=-.5; k1:=0.1; k2:=0.4; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=0.5,k2); > k:=khaar+0.005*kmexh; > plot(k,x=0..1,title='k'); Mexican hat - Haar basis heat conductivity contrast variability > restart; sig:=-.5; k1:=contrast*k2; k2:=0.05; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=0.5,k2); > k:=khaar+0.005*kmexh; > plot3d(k,x=0..1,contrast=5..100,title='k'); Spatial averaging of the Mexican hat - Haar type heat conducitivity > restart; sig:=-.5; k1:=0.1; k2:=0.4; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=0.5,k2); > k:=khaar+0.005*kmexh; > plot(k,x=0..1,title='k'); > kav:=evalf(int(k,x=0..1)); Classical homogenisation of the Mexican hat - Haar basis type heat conductivity > restart; sig:=-.5; k1:=0.1; k2:=0.4;

Appendix 391 kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig 2)))*(x 2/sig 2-1)); >khaar:=piecewise(x=0.5,k2); >k:=khaar+0.005*kmexh; >kk:=1/k:kkk:=int(kk,x=0..1):khom:=evalf(1/kkk); Wavelet homogenisation of the Mexican hat-Haar basis type heat conductivity >restart;sig=-.5;k1:=0.1;k2:=0.4; >kmexh:=2+1/(sqrt(2*P1)*sig3)*(exp(-x2/(2*sig2))'(x2/sig2-1): >khaar:=piecewise(x=0.5,k2); k:=khaar+0.005*kmexh: >kk:=1/k;kkk:=x/k;kkkk:=1/(2*k); kkk1:=evalf(int(kk,x=0..1));kkk2:=evalf(int(kkk,x=0..1)); kkk3:=evalf(int(kkkk,x=0..1)); khomwav:=evalf(1/(kkk1-2*kkk2+2*kkk3)); Parametric variability of the spatial average of the Mexican hat-Haar type heat conductivity with respect to the contrast and volumetric ratio restart;sig:=-.5;k1:=contrast*k2;k2:=0.05; kmexh:=2+1/(sqrt(2*Pi)*sig 3)*((exp(-x^2/(2*sig 2)))*(x 2/sig 2-1)); khaar:=piecewise(x=g,k2); >k:=khaar+0.005*kmexh; >kav:=evalf(int(k,x=0..1)); >plot3d(kav,contrast=5..100,g=0.1..0.9,title='kav'); Parametric sensitivity of the Mexican hat-Haar basis effective heat conductivity with respect to the contrast and volumetric ratio restart;sig:=-.5;k1:=contrast*k2;k2:=0.05; kmexh:=2+1/(sqrt(2*Pi)*sig 3)*((exp(-x 2/(2*sig 2)))*(x^2/sig 2-1)); khaar:=piecewise(x=g,k2); k:=khaar+0.005*kmexh: >kav:=evalf(int(k,x=0..1)); dkavdcontrast:=diff(kav,contrast)*contrast/kav; >plot3d(dkavdcontrast,contrast=5..100,g=0.1..0.9,title='dkavdcontrast'); dkavdg:=diff(kav,g)"g/kav; >plot3d(dkavdg,contrast=5..100,g=0.1..0.9,title='dkavdg'); Parametric variability of the classically homogenised the Mexican hat-Haar basis heat conductivity with respect to the contrast and volumetric ratio restart;sig:=-.5;k1:=contrast*k2;k2:=0.05; kmexh:=2+1/(sqrt(2*Pi)*sig 3)*((exp(-x 2/(2*sig 2)))*(x^2/sig 2-1)); >khaar:=piecewise(xg,k2); >k:=khaar+0.005*kmexh;
Appendix 391 > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=0.5,k2); > k:=khaar+0.005*kmexh; > kk:=1/k: kkk:=int(kk,x=0..1): khom:=evalf(1/kkk); Wavelet homogenisation of the Mexican hat - Haar basis type heat conductivity > restart; sig:=-.5; k1:=0.1; k2:=0.4; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=0.5,k2); > k:=khaar+0.005*kmexh; > kk:=1/k; kkk:=x/k; kkkk:=1/(2*k); > kkk1:=evalf(int(kk,x=0..1)); kkk2:=evalf(int(kkk,x=0..1)); kkk3:=evalf(int(kkkk,x=0..1)); > khomwav:=evalf(1/(kkk1-2*kkk2+2*kkk3)); Parametric variability of the spatial average of the Mexican hat - Haar type heat conductivity with respect to the contrast and volumetric ratio > restart; sig:=-.5; k1:=contrast*k2; k2:=0.05; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=g,k2); > k:=khaar+0.005*kmexh; > kav:=evalf(int(k,x=0..1)); > plot3d(kav,contrast=5..100,g=0.1..0.9,title='kav'); Parametric sensitivity of the Mexican hat - Haar basis effective heat conductivity with respect to the contrast and volumetric ratio > restart; sig:=-.5; k1:=contrast*k2; k2:=0.05; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(x=g,k2); > k:=khaar+0.005*kmexh; > kav:=evalf(int(k,x=0..1)); > dkavdcontrast:=diff(kav,contrast)*contrast/kav; > plot3d(dkavdcontrast,contrast=5..100,g=0.1..0.9,title='dkavdcontrast'); > dkavdg:=diff(kav,g)*g/kav; > plot3d(dkavdg,contrast=5..100,g=0.1..0.9,title='dkavdg'); Parametric variability of the classically homogenised the Mexican hat - Haar basis heat conductivity with respect to the contrast and volumetric ratio > restart; sig:=-.5; k1:=contrast*k2; k2:=0.05; > kmexh:=2+1/(sqrt(2*Pi)*sig^3)*((exp(-x^2/(2*sig^2)))*(x^2/sig^2-1)); > khaar:=piecewise(xg,k2); > k:=khaar+0.005*kmexh;