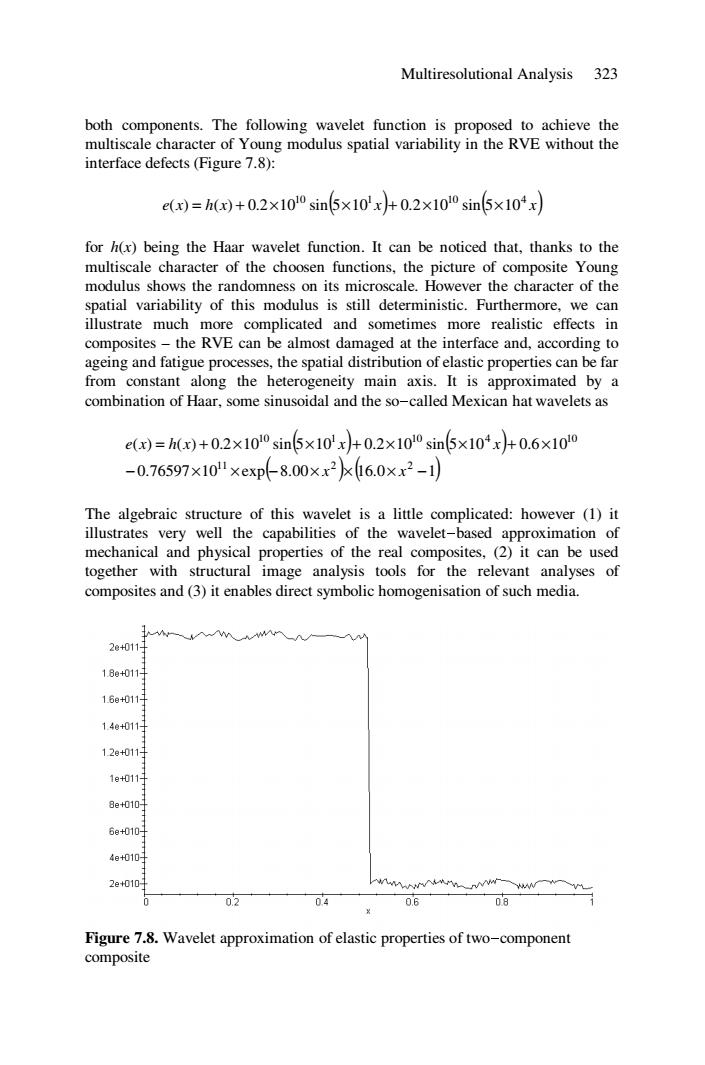
Multiresolutional Analysis 323 both components.The following wavelet function is proposed to achieve the multiscale character of Young modulus spatial variability in the RVE without the interface defects (Figure 7.8): e()=h(w)+0.2×100sin5×10'x+0.2x100sin5×104x for h(x)being the Haar wavelet function.It can be noticed that,thanks to the multiscale character of the choosen functions,the picture of composite Young modulus shows the randomness on its microscale.However the character of the spatial variability of this modulus is still deterministic.Furthermore,we can illustrate much more complicated and sometimes more realistic effects in composites-the RVE can be almost damaged at the interface and,according to ageing and fatigue processes,the spatial distribution of elastic properties can be far from constant along the heterogeneity main axis.It is approximated by a combination of Haar,some sinusoidal and the so-called Mexican hat wavelets as e()=h(x)+0.2×100sin5×10'x+0.2x10l0si5×104x+0.6×100 -0.76597×10l×exp8.00×x2kl6.0xx2-1 The algebraic structure of this wavelet is a little complicated:however (1)it illustrates very well the capabilities of the wavelet-based approximation of mechanical and physical properties of the real composites,(2)it can be used together with structural image analysis tools for the relevant analyses of composites and(3)it enables direct symbolic homogenisation of such media. 2e+011 18e+011- 16e+011 14e+011] 12g+011月 1g+011 8e+0101 6e+010- 4e+010月 2e+0101 0.2 04 0.6 5 Figure 7.8.Wavelet approximation of elastic properties of two-component compositeMultiresolutional Analysis 323 both components. The following wavelet function is proposed to achieve the multiscale character of Young modulus spatial variability in the RVE without the interface defects (Figure 7.8): e x h x ( x) ( x) 10 1 10 4 ( ) = ( ) + 0.2×10 sin 5×10 + 0.2×10 sin 5×10 for h(x) being the Haar wavelet function. It can be noticed that, thanks to the multiscale character of the choosen functions, the picture of composite Young modulus shows the randomness on its microscale. However the character of the spatial variability of this modulus is still deterministic. Furthermore, we can illustrate much more complicated and sometimes more realistic effects in composites – the RVE can be almost damaged at the interface and, according to ageing and fatigue processes, the spatial distribution of elastic properties can be far from constant along the heterogeneity main axis. It is approximated by a combination of Haar, some sinusoidal and the so-called Mexican hat wavelets as () ( ) 0.76597 10 exp( )( ) 8.00 16.0 1 ( ) ( ) 0.2 10 sin 5 10 0.2 10 sin 5 10 0.6 10 11 2 2 10 1 10 4 10 − × × − × × × − = + × × + × × + × x x e x h x x x The algebraic structure of this wavelet is a little complicated: however (1) it illustrates very well the capabilities of the wavelet-based approximation of mechanical and physical properties of the real composites, (2) it can be used together with structural image analysis tools for the relevant analyses of composites and (3) it enables direct symbolic homogenisation of such media. Figure 7.8. Wavelet approximation of elastic properties of two-component composite