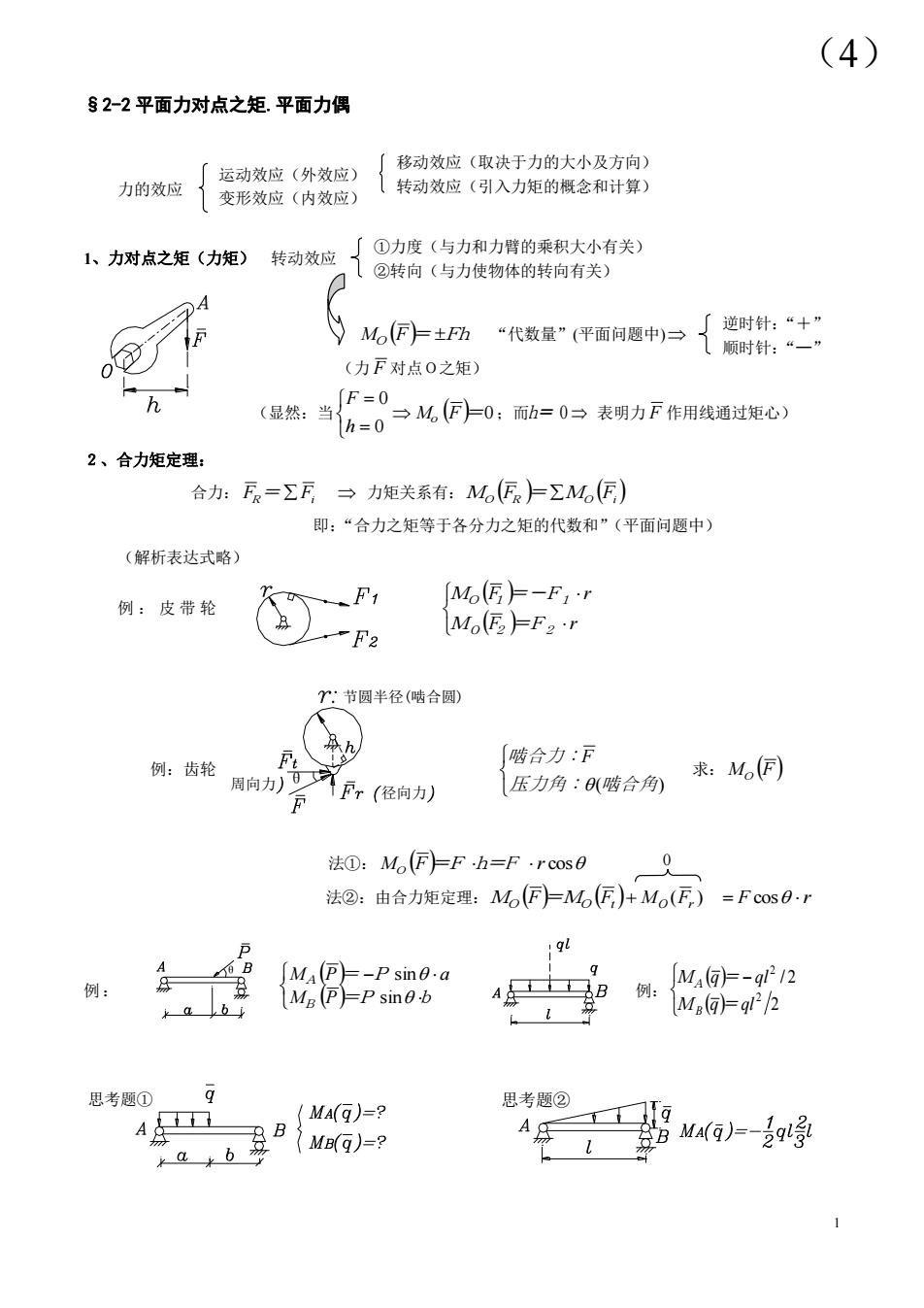
(4) $2-2平面力对点之矩.平面力偶 运动效应（外效应） 移动效应（取决于力的大小及方向） 力的效应 变形效应（内效应） 转动效应（引入力矩的概念和计算） 人方树点之矩功矩转司他{8的商《衡力胞物钠衡价南关 (历代数室伴面月题户{：生 (力F对点0之矩) (显然：当F=0 一M(匣=0：而h=0一表明力F作用线通过矩心) h=0 2、合力矩定理： 合力：F=∑F→力矩关系有：M(匠R上∑M(匠) 即：“合力之矩等于各分力之矩的代数和”（平面问题中） (解析表达式略》 例：皮带轮 Mo F=-Fr Mo(E上F2r 了：节圆半径（啮合圆） h 「啮合力：F 例：齿轮 求：Mo(F) 压力角：（啮合 法①：Mo(FFh=F·rcos0 法②：由合力矩定理：M(厅M(匠)+Mo(F)=Fcos0r M片 -P sin0.a M(@=-g212 Mg (PP sine-b 4合马B例： M@g22 思考题① 4 (MA()=? 思考题② A 出M4()=- 1 0 §2-2 平面力对点之矩.平面力偶 力的效应 1、力对点之矩（力矩） 转动效应 MＯ F＝ Ｆｈ “代数量”(平面问题中)  （力 F 对点Ｏ之矩） （显然：当   0 0 0 M F ＝ h F  ｏ      ；而 ｈ＝ 0  表明力 F 作用线通过矩心） ２、合力矩定理： 合力： FＲ ＝  Fi  力矩关系有：     ＭＯ FＲ ＝ ＭＯ Fi 即：“合力之矩等于各分力之矩的代数和”（平面问题中） （解析表达式略） 例 ： 皮 带 轮          Ｍ F ＝Ｆ r Ｍ F ＝－Ｆ r O ２ ２ Ｏ １ １ 例：齿轮    压力角： (啮合角) 啮合力：F  求： M F  Ｏ 法①： MＯ F＝Ｆ ｈ＝F r cos 法②：由合力矩定理：     ( ) ＭＯ F ＝ＭＯ Ft  MO Fr  F cos r 例：           M P ＝Ｐ ｂ M P ＝ Ｐ a Ｂ Ａ   sin sin 例：         2 / 2 2 2 Ｍ q ＝ ql Ｍ q ＝ ql B Ａ θ 径向力 节圆半径(啮合圆) 周向力 θ 思考题① 思考题② 运动效应（外效应） 变形效应（内效应） 移动效应（取决于力的大小及方向） 转动效应（引入力矩的概念和计算） ①力度（与力和力臂的乘积大小有关） ②转向（与力使物体的转向有关） 逆时针：“＋” 顺时针：“—” （4）