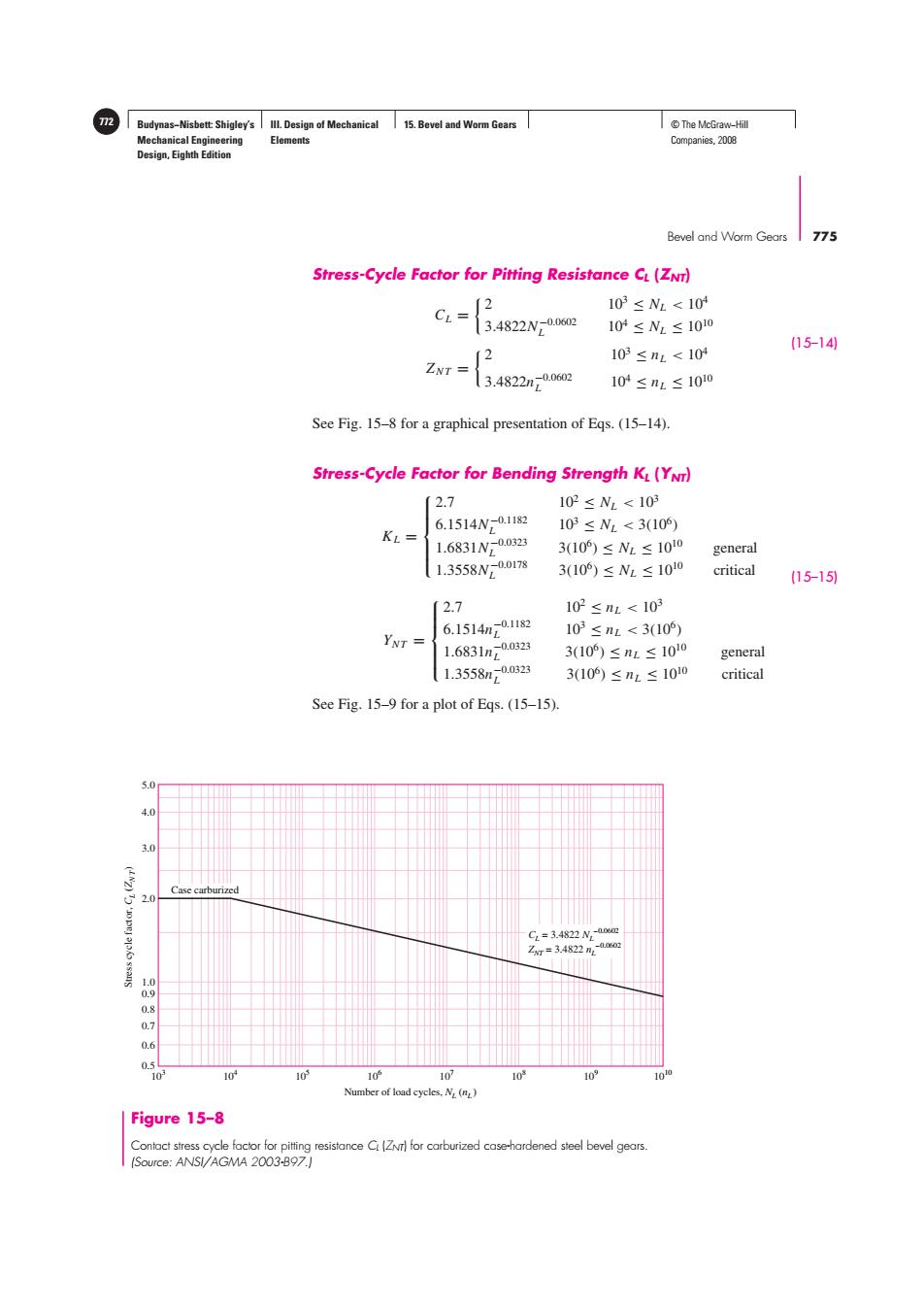
Budynas-Nisbett:Shigley's Ill.Design of Mechanical 15.Bevel and Worm Gears ©The McGraw-Hill Mechanical Engineering Elements Companies,2008 Design,Eighth Edition Bevel and Worm Gears 775 Stress-Cycle Factor for Pitting Resistance CL(ZNT) 2 CL= 103≤Wz<10 3.4822W0.0602 104≤Nz≤1010 (15-14 2 103≤nL<104 3.4822m20.0602 104≤nL≤1010 See Fig.15-8 for a graphical presentation of Eqs.(15-14). Stress-Cycle Factor for Bending Strength KL(YNT) 2.7 102≤N2<103 103≤N2<3(10) KL= 6.1514W01182 1.6831W00323 3(10)≤Nz≤1010 general 1.3558W00178 3(10)≤WL≤1010 critical (15-15) 2.7 102≤nL<103 YNT 6.1514n20.1182 103≤nL<3(10) 1.6831n0.0323 3(10)≤nL≤1010 general 1.3558m-0.0323 3(10)≤nL≤1010 critical See Fig.15-9 for a plot of Eqs.(15-15). 5.0 ￥0 3.0 Case carburized 2.0 C2=3.4822N-m Zr=3.4822n2 1.0 e 103 10 10 10 107 103 10 10 Number of load cycles.N (n) Figure 15-8 Contact stress cycle factor for pitting resistance CZNr)for carburized case-hardened steel bevel gears. (Source:ANSI/AGMA 2003-B97.)Budynas−Nisbett: Shigley’s Mechanical Engineering Design, Eighth Edition III. Design of Mechanical Elements 15. Bevel and Worm Gears 772 © The McGraw−Hill Companies, 2008 Bevel and Worm Gears 775 Stress cycle factor, CL (ZNT) Number of load cycles, NL (nL ) 104 103 0.5 0.6 0.7 0.8 0.9 1.0 2.0 3.0 4.0 5.0 105 106 107 108 109 1010 Case carburized CL = 3.4822 NL –0.0602 ZNT = 3.4822 nL –0.0602 Figure 15–8 Contact stress cycle factor for pitting resistance CL (ZNT) for carburized case-hardened steel bevel gears. (Source: ANSI/AGMA 2003-B97.) Stress-Cycle Factor for Pitting Resistance CL (ZNT) CL =  2 103 ≤ NL < 104 3.4822N −0.0602 L 104 ≤ NL ≤ 1010 ZN T =  2 103 ≤ nL < 104 3.4822n−0.0602 L 104 ≤ nL ≤ 1010 (15–14) See Fig. 15–8 for a graphical presentation of Eqs. (15–14). Stress-Cycle Factor for Bending Strength KL (YNT) KL = ⎧ ⎪⎪⎪⎨ ⎪⎪⎪⎩ 2.7 102 ≤ NL < 103 6.1514N −0.1182 L 103 ≤ NL < 3(106) 1.6831N −0.0323 L 3(106) ≤ NL ≤ 1010 general 1.3558N −0.0178 L 3(106) ≤ NL ≤ 1010 critical (15–15) YN T = ⎧ ⎪⎪⎪⎨ ⎪⎪⎪⎩ 2.7 102 ≤ nL < 103 6.1514n−0.1182 L 103 ≤ nL < 3(106) 1.6831n−0.0323 L 3(106) ≤ nL ≤ 1010 general 1.3558n−0.0323 L 3(106) ≤ nL ≤ 1010 critical See Fig. 15–9 for a plot of Eqs. (15–15)