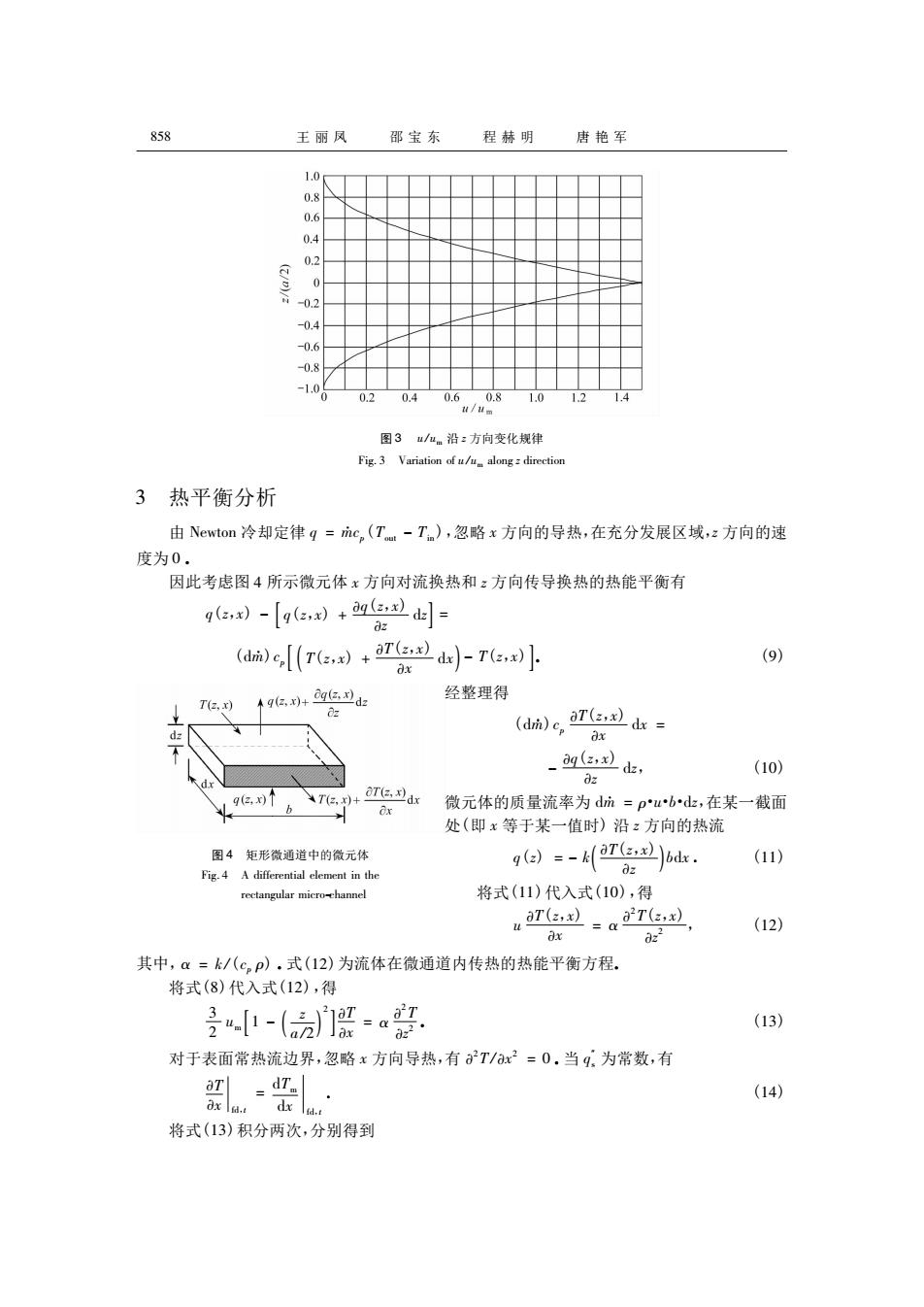
王丽风 邵宝东程赫明唐艳军 0 -08 -1.0 1.0 12 图3ua.沿：方向变化规律 3热平衡分析 由Newton冷却定律q=c,(T-T),忽略x方向的导热，在充分发展区域，z方向的速 府为0， 因此考虑图4所示微元体x方向对流换热和：方向传导换热的热能平衡有 )-9()+= aclreo+r2-rtl (9) 经整理得 (dm),ard (10) 、、 ds. 微元体的质量流率为dm=pubd止，在某一截面 处（即x等于某一值时）沿：方向的热流 图4矩形微通逍中的微元体 a. (11) 将式(11)代入式(10)，得 (12) 其中，a=k/(c,p）),式(12)为流体在微通道内传热的热能平衡方程。 将式(8)代入式(12)，得 是-(]臣= (13) 对于表面常热流边界，忽略x方向导热，有T/a2=0.当g为常数，有 (14) 将式(13)积分两次，分别得到 图 3 u /um 沿 z 方向变化规律 Fig． 3 Variation of u /um along z direction 3 热平衡分析 由 Newton 冷却定律 q = mcp ( Tout － Tin ) ，忽略 x 方向的导热，在充分发展区域，z 方向的速 度为 0 ． 因此考虑图 4 所示微元体 x 方向对流换热和 z 方向传导换热的热能平衡有 q( z，x) － q( z，x) + q( z，x) z [ ] dz = ( dm) cp T( z，x) + T( z，x) x ( ) dx － T( z，x [ ] ) ． ( 9) 图 4 矩形微通道中的微元体 Fig． 4 A differential element in the rectangular micro-channel 经整理得 ( dm) cp T( z，x) x dx = － q( z，x) z dz， ( 10) 微元体的质量流率为 dm = ρ·u·b·dz，在某一截面 处( 即 x 等于某一值时) 沿 z 方向的热流 q( z) = － k T( z，x)  ( ) z bdx ． ( 11) 将式( 11) 代入式( 10) ，得 u T( z，x) x = α  2 T( z，x) z 2 ， ( 12) 其中，α = k /( cp ρ) ． 式( 12) 为流体在微通道内传热的热能平衡方程． 将式( 8) 代入式( 12) ，得 3 2 um 1 － z a / ( ) 2 [ ] 2 T x = α  2 T z 2 ． ( 13) 对于表面常热流边界，忽略 x 方向导热，有  2 T /x 2 = 0 ． 当 q″ s 为常数，有 T x fd，t = dTm dx fd，t ． ( 14) 将式( 13) 积分两次，分别得到 858 王 丽 凤 邵 宝 东 程 赫 明 唐 艳 军