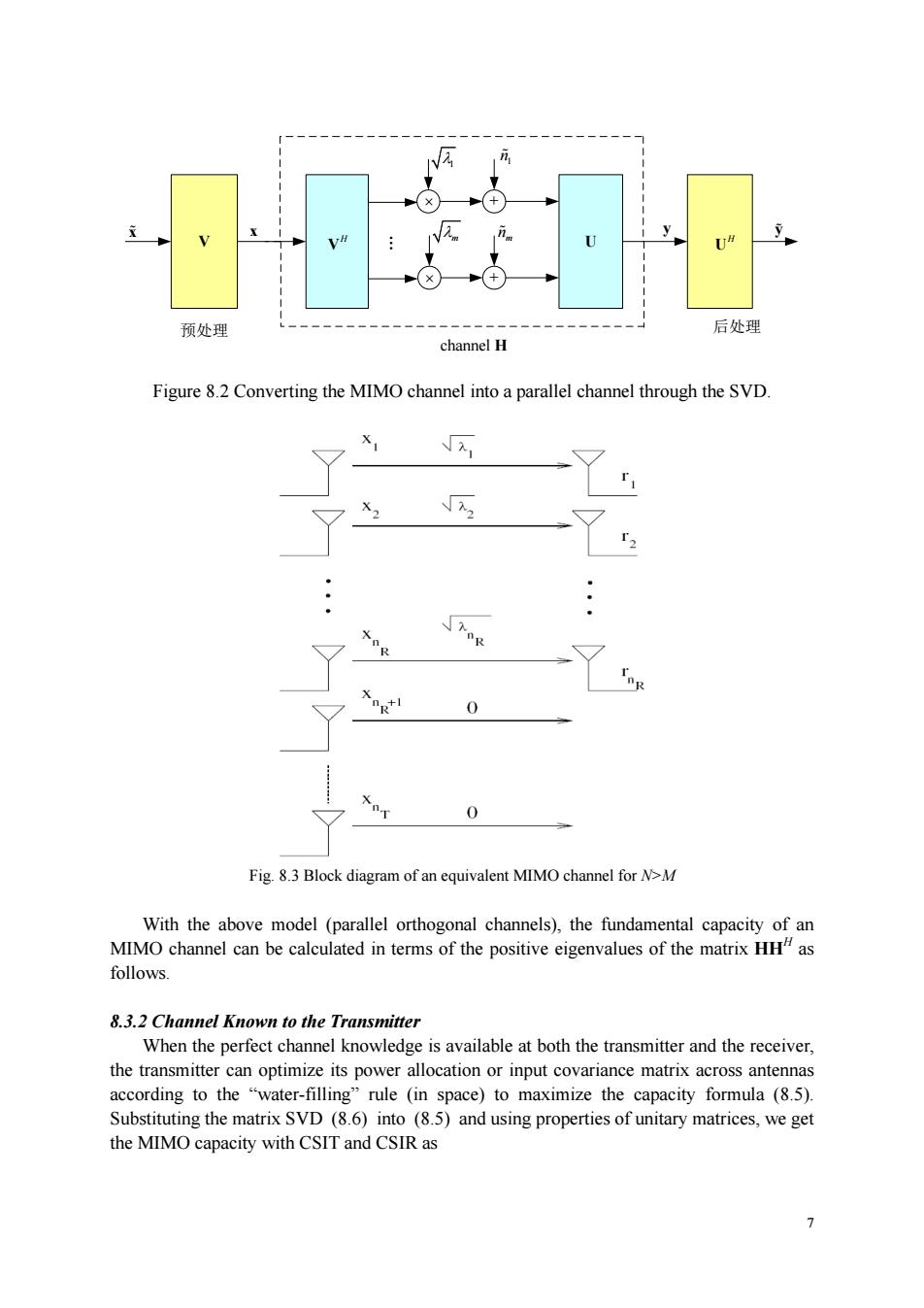
日 channel H Figure 8.2 Converting the MIMO channel into a parallel channel through the SVD. X r Xog'I 0 0 Fig.8.3 Block diagram of an equivalent MIMO channel for N>M With the above model (parallel orthogonal channels),the fundamental capacity of an MIMO channel can be cale ated in terms of the positive eigenvalues of the matrix HHas follows 8.3.2 Channel Known to the Transmitter When the perfect channel knowledge is available at both the transmitter and the receiver, the transmitter according to the Substituting the matrix SVD (8.6)into (8.5)and using properties of unitary matrices,we get the MIMO capacity with CSIT and CSIR as 7 7 V U x H V .   + + H U 1 m 1 n mn y 预处理 后处理 channel H x y Figure 8.2 Converting the MIMO channel into a parallel channel through the SVD. Fig. 8.3 Block diagram of an equivalent MIMO channel for N>M With the above model (parallel orthogonal channels), the fundamental capacity of an MIMO channel can be calculated in terms of the positive eigenvalues of the matrix HHH as follows. 8.3.2 Channel Known to the Transmitter When the perfect channel knowledge is available at both the transmitter and the receiver, the transmitter can optimize its power allocation or input covariance matrix across antennas according to the “water-filling” rule (in space) to maximize the capacity formula (8.5). Substituting the matrix SVD (8.6) into (8.5) and using properties of unitary matrices, we get the MIMO capacity with CSIT and CSIR as