
0122229现代数字通信与编码理论 December 20,2008 XDU,Winter 2008 Lecture Notes Chapter 8 Space-Time Coded-Modulation for Multiple Antenna Systems (/for MIMO Channels) The advent of multiple-input-multiple-output (MIMO)space-time coded wireless systems has recently emerged as one of the most significant technical breakthroughs in modern communications.The research on MIMO systems,including the study of channel requirement of increasing bandwidth and transmit power). Note:The materials presented in Sections 8.3 and 8.6.3 are based largely on B.Vucetic's lecture notes. 8.1 Introduction An MIMO system is an arbitrary wireless communication system in which the transmitter as well as the receiver is equipped with multiple antenna elements.A core idea in MIMO systems is space-time signal processing in which time is complemented with the spatial dimension inherent in the use of multiple spatially distributed ntennas.MIMO effectively takes advantage of rand ng and multipath delay 图81给出了 read for ing transfer rate 有N根发送天线、M根接收天线的MMO系统框图。下图是采用不 同天线配置时的通信系统。 SISO MIMO TX/R< 乙RxWX SIMO MIMO-MU MISO Figure 8.0 Different antenna configurations in space-time systems
1 0122229 现代数字通信与编码理论 December 20, 2008 XDU, Winter 2008 Lecture Notes Chapter 8 Space-Time Coded-Modulation for Multiple Antenna Systems (/for MIMO Channels) The advent of multiple-input–multiple-output (MIMO) space-time coded wireless systems has recently emerged as one of the most significant technical breakthroughs in modern communications. The research on MIMO systems, including the study of channel capacity and the design of communication schemes, demonstrates that MIMO systems have a potential to significantly increase spectral efficiency in wireless communications (without the requirement of increasing bandwidth and transmit power). Note: The materials presented in Sections 8.3 and 8.6.3 are based largely on B. Vucetic’s lecture notes. 8.1 Introduction An MIMO system is an arbitrary wireless communication system in which the transmitter as well as the receiver is equipped with multiple antenna elements. A core idea in MIMO systems is space-time signal processing in which time is complemented with the spatial dimension inherent in the use of multiple spatially distributed antennas. MIMO effectively takes advantage of random fading and multipath delay spread for multiplying transfer rates. 图 8.1 给出了一个有 N 根发送天线、M 根接收天线的 MIMO 系统框图。下图是采用不 同天线配置时的通信系统。 Figure 8.0 Different antenna configurations in space-time systems

Winter、Foschini和Telatar的开创性工作证明,多天线阵技术可极大的提高系统信 道容量。若接收端可准确估计信道信息,并保证不同发射接收天线对之间的信道衰落 系数相互独立,则一个拥有N根发射天线和M根接收天线的MMO系统的信道容量将 随mi{MN线性增加。因此,信噪比、发射功率和信道带宽都相同时,多天线系统可 提供的信道容量是单天线系统的mi(M倍。在频率资源日益紧张的今天,多天线信 道容量理论无疑给解决高速无线通信问题开辟了一条新思路,基于此发展起来的信道编 码和信号处理技术正越来越受到人们的关注。 8.2 MIMO System Model nmunication system with N transmit and Mreceive The transmitted signal at time is represented by an Nx1 column vector xeC,and the received signal is represented by an Mx1 column vector yC(For simplicity,we ignore the time index).The discrete-time MIMOchannel can be described by y=Hx+n (8.1) where H is an MxN complex matrix describing the channel and the elementh,of H represents the channel gain from the transmit antenna to the receive antenna and n(0.N)is a zero-mean complex Gaussian noise vector whose components are ii.d.circularly symmetric complex Gaussian variables.The covariance matrix of the noise is given by KEnn]=N=,i.e.,each of Mreceive antennas has identical noise power of No(per complex dimension)(or,per real dimension).The total transmitted power is constrained to P,regardless of the number of transmit antennas N.It can be represented as Ex=E[xx]=E[Tr(x")]=TrEfxx=tr(K)sP. where K=Exxis the covariance matrix of the transmitted signal x.Furthermore,if the channel is unknown to the transmitter,we assume that the signals transmitted from individual antennas have equal powers of P/N.It means that K.= (8.2) The received signal covariance matrix,defined as K,=Eyy,is given by K,=Eyy"=HK,H"+NoI Denoting by P the average signal power at the output of each receive antenna,the average
2 Winter、Foschini 和 Telatar 的开创性工作证明,多天线阵技术可极大的提高系统信 道容量。若接收端可准确估计信道信息,并保证不同发射-接收天线对之间的信道衰落 系数相互独立,则一个拥有 N 根发射天线和 M 根接收天线的 MIMO 系统的信道容量将 随 min{M, N}线性增加。因此,信噪比、发射功率和信道带宽都相同时,多天线系统可 提供的信道容量是单天线系统的 min(M, N)倍。在频率资源日益紧张的今天,多天线信 道容量理论无疑给解决高速无线通信问题开辟了一条新思路,基于此发展起来的信道编 码和信号处理技术正越来越受到人们的关注。 8.2 MIMO System Model Consider a single-user MIMO communication system with N transmit and M receive antennas. (It will be called a (N, M) system.) The system block diagram is shown in Fig.8.1. The transmitted signal at time t is represented by an N1 column vector N x , and the received signal is represented by an M1 column vector M y (For simplicity, we ignore the time index). The discrete-time MIMO channel can be described by y Hx n (8.1) where H is an MN complex matrix describing the channel and the element ij h of H represents the channel gain from the transmit antenna j to the receive antenna i; and 0 , n 0I N M is a zero-mean complex Gaussian noise vector whose components are i.i.d. circularly symmetric complex Gaussian variables. The covariance matrix of the noise is given by 2 0 [] 2 H K nn I I n MM E N , i.e., each of M receive antennas has identical noise power of N0 (per complex dimension) (or, 2 per real dimension). The total transmitted power is constrained to P, regardless of the number of transmit antennas N. It can be represented as 2 || || ( ) tr( ) HHH Tr Tr P x E EE E K x x x xx xx , where = H x K xx E is the covariance matrix of the transmitted signal x. Furthermore, if the channel is unknown to the transmitter, we assume that the signals transmitted from individual antennas have equal powers of P/N. It means that x N P N K I (8.2) The received signal covariance matrix, defined as = H y K E yy , is given by 0 H H y xM N K E yy HK H I Denoting by Pr the average signal power at the output of each receive antenna, the average

SNR at each receive antenna is given by SNR-7-N. which is independent of N.The total received signal power can be expressed asTr(K) h 7 h 2 空时 ④ 空时 发送 接收 ny Fig.8.1 An MIMO wireless system model We will consider several possible scenarios for the matrix H: 1.H is deterministic 2.H is a random matrix.Its entries are selected according a probability distribution at the beginning of each symbol interval T and are kept constant during one symbol interval.In each of the cha corresp ding to an inc dependent ealization of H. ing channel. 3.H is a random matrix.Its entries change randomly and are kept constant during a fixed number of symbol intervals,much shorter than a transmission block.Such a channel is called a block fading channel. 4.H is a random matrix but is fixed at the start of a transmission block and kept constant Such a channel is called a slow or quasi-static fading channel For normalization purposes,we assume that the received power for each of M receive branches is equal to the total transmitted power.Thus,in the case when H is deterministic,we have F-N.n.2. When H is random,we will assume that its entries are i.i.d.zero-mean complex Gaussian with variance per dimension.This scase is usually referred to as a rich scattering environmen.The normalization constraint for the elements of H is given by 2E[h门=N,m=l2M
3 SNR at each receive antenna is given by 0 Pr N SNR which is independent of N. The total received signal power can be expressed asTr( ) K y . Fig. 8.1 An MIMO wireless system model We will consider several possible scenarios for the matrix H: 1. H is deterministic. 2. H is a random matrix. Its entries are selected according a probability distribution at the beginning of each symbol interval T and are kept constant during one symbol interval. In other words, each use of the channel corresponding to an independent realization of H. Such a channel is called a fast (or independent) fading channel. 3. H is a random matrix. Its entries change randomly and are kept constant during a fixed number of symbol intervals, much shorter than a transmission block. Such a channel is called a block fading channel. 4. H is a random matrix but is fixed at the start of a transmission block and kept constant during a transmission block. Such a channel is called a slow or quasi-static fading channel. For normalization purposes, we assume that the received power for each of M receive branches is equal to the total transmitted power. Thus, in the case when H is deterministic, we have 2 1 | | , 1,2,., N mn n h Nm M When H is random, we will assume that its entries are i.i.d. zero-mean complex Gaussian variables, each with variance 1/2 per dimension. This case is usually referred to as a rich scattering environment. The normalization constraint for the elements of H is given by 2 1 | | , 1,2,., N mn n h Nm M E

With the normalization constraint,the total received signal power per antenna is equal to the total transmitted power,and the average SNR at any receive antenna isy=P/N. In all cases,we will assume that the channel matrix is known to the receiver(ie.,perfect CSIR),equivalently,the channel output consists of the pair(y,H),and the distribution of H is known at the transmitter.In most situations,the realization of H(CSI)is assumed to be not known at the transmitter. 8.3 Fundamental Capacity Limits of MIMO Channels Consider the case of deterministic H.The channel matrix H is assumed to be constant at all time and known to the receiver.The relation of(8.1)indicates a vector Gaussian channel. The Shannon capacity is defined as the maximum data rate that can be transmitted over the mation C(H)= mZ,田=m8xZx+Zxy田 =max Z(x;y H)=max [H(yH)-H(ylx,H)] (8.3) where p(x)is the probability distribution of the vector x,H(y|H)and H(yx,H)are the differential entropy and the conditional differential entropy of the vector y,respectively.Since the vectors x and n are independent,we have Hylx,H)=H(n)=log2(det(πeW。Iy) which has fixed value and is independent of the channel input.Thus,maximizing the mutual information I(x:y|H)is equivalent to maximize H(yH).From (8.1),the covariance matrix ofy is K,=E["]=HKH"+N。Iw Among all vectors y with a given covariance matrix K.the differential entropy H(y)is maximized when y is a zero-mean circularly symmetric complex Gaussian (ZMCSCG) random vector [Telatar9].This implies that the inputx must also be ZMCSCG and therefore this is the optimal distribution onx.This yields the entropy H(yH)given by H(y|H)=log,(det(eK,)) The mutual information then reduces to Z(x:y|H)=H(y|H)-H(n) log,det (8.4)
4 With the normalization constraint, the total received signal power per antenna is equal to the total transmitted power, and the average SNR at any receive antenna is 0 P N/ . In all cases, we will assume that the channel matrix is known to the receiver (i.e., perfect CSIR), equivalently, the channel output consists of the pair (y, H), and the distribution of H is known at the transmitter. In most situations, the realization of H (CSI) is assumed to be not known at the transmitter. 8.3 Fundamental Capacity Limits of MIMO Channels Consider the case of deterministic H. The channel matrix H is assumed to be constant at all time and known to the receiver. The relation of (8.1) indicates a vector Gaussian channel. The Shannon capacity is defined as the maximum data rate that can be transmitted over the channel with arbitrarily small error probability. It is given in terms of the mutual information between vectors x and y as 2 ( ): [|| || ] ( ) ( ) max ( ; , ) max ( ; ) ( ; | ) p P p x C x x H x y H xH x y H E () () max ( ; | ) max ( | ) ( | , ) px px x y H y H y x H (8.3) where p(x) is the probability distribution of the vector x, ( | ) and ( | , ) y H y x H are the differential entropy and the conditional differential entropy of the vector y, respectively. Since the vectors x and n are independent, we have ( | , ) ( ) log det( ) y xH n I 2 0 eN M which has fixed value and is independent of the channel input. Thus, maximizing the mutual information ( ; | ) x y H is equivalent to maximize ( | ) y H . From (8.1), the covariance matrix of y is = 0 H H y xM N K E K yy HH I Among all vectors y with a given covariance matrix Ky, the differential entropy ( ) y is maximized when y is a zero-mean circularly symmetric complex Gaussian (ZMCSCG) random vector [Telatar99]. This implies that the input x must also be ZMCSCG, and therefore this is the optimal distribution on x. This yields the entropy ( | ) y H given by ( | ) log det( ) y H 2 eK y The mutual information then reduces to (; | ) ( | ) () x y H y H n 2 0 1 log det H M x N I HH K (8.4)

where we have used the fact that det(AB)=det(A)det(B)and det(A-)=[det(A)].And the MIMO capacity is given by maximizing the mutual information (8.4)over all input covariance matrces K,satistying the power constraint c器,ogda+Kr》 bits per channel use (8.5) -腮a+之kr列 where the last equality follows from the fact that det(I+AB)=det(I+BA)for matrices A(mxm)andB(n×m) Clearly,the optimization relative to K.will depend on whether or not H is known at the transmitter.We now discuss this maximizing under different assumptions about transmitter CSI by decomposing the vector channel into a set of parallel,independent scalar Gaussian sub-channels. 8.3.1 Parallel Decomposition of the MIMO Channel By the singular value decomposition(SVD)theorem,any MxN matrix HECN can be written as H=UAVI (8.6) where A is an MN non-negative real and diagonal matrix.U and V are MxM and NxN unitary matrices,respectively.That is.UU=I and VV=where the superseript entries of A are the non-negat e columns of U are the eigenvectors of HH and the columns of Vare the eigenvectors of HH. Denote by Athe eigenvalues of HH",which are defined by HH"z=z,z0 (87) mber of no cannot exceed the number of columns or rows of H,rsm=min(M,N).If H is full rank, which is sometimes referred to as a rich scattering environment,thenr=m.Equation (8.7) can be rewritten as (2L.-W)z=0,z0 (8.8) where W is the Wishart matrix defined to be 5
5 where we have used the fact that det( ) det( )det( ) AB A B and 1 1 det( ) det( ) A A . And the MIMO capacity is given by maximizing the mutual information (8.4) over all input covariance matrces Kx satisfying the power constraint: 2 :( ) 0 1 ( ) max log det x x H M x Tr P C N H I HH K K K bits per channel use (8.5) 2 :( ) 0 1 max log det x x H N x Tr P N I HH K K K where the last equality follows from the fact that det det I AB I BA m n for matrices A B ( ) and ( ) mn nm . Clearly, the optimization relative to Kx will depend on whether or not H is known at the transmitter. We now discuss this maximizing under different assumptions about transmitter CSI by decomposing the vector channel into a set of parallel, independent scalar Gaussian sub-channels. 8.3.1 Parallel Decomposition of the MIMO Channel By the singular value decomposition (SVD) theorem, any MN matrix M N H can be written as H H U ΛV (8.6) where is an MN non-negative real and diagonal matrix, U and V are MM and NN unitary matrices, respectively. That is, and H H UU I VV I M N , where the superscript “H” stands for the Hermitian transpose (or complex conjugate transpose). In fact, the diagonal entries of are the non-negative square roots of the eigenvalues of matrix HHH, the columns of U are the eigenvectors of HHH and the columns of V are the eigenvectors of HHH. Denote by the eigenvalues of HHH, which are defined by H HH z z , z0 (8.7) where z is an M1 eigenvector corresponding to . The number of non-zero eigenvalues of matrix HHH is equal to the rank of H. Let r be the rank of the matrix H. Since the rank of H cannot exceed the number of columns or rows of H, min( , ) r m MN . If H is full rank, which is sometimes referred to as a rich scattering environment, then r = m. Equation (8.7) can be rewritten as ( ) 0, I Wz m z0 (8.8) where W is the Wishart matrix defined to be

w=H”,ifMm,do not depend on the transmitted signal.On the other hand,received componentsi=1,2,.m depend only the transmitted component ,Thus the equivalent MIMO channel in (8.10)can be considered as consisting of m uncoupled parallel Gaussian sub-channels.Specifically, If N>M (8.11)indicates that there will be at most M non-zero attenuation subchannels in the equivalent MIMO channel.See Fig.8.3 If N.there will be at most N non-zero attenuation subchannels in the equivalent MIMO channel
6 , if , if H H M N M N HH W H H This implies that det( ) 0 I W m (8.9) The m nonzero eigenvalues of W, 1, 2, ., m, can be calculated by finding the roots of (8.9). The non-negative square roots of the eigenvalues of W are also referred to as singular values of H. Substituting (8.6) into (8.1), we have H y U ΛVx n Let , , HHH y U y x Vxn Un . Note that U and V are invertible, n and n have the same distribution (i.e., zero-mean Gaussian with i.i.d. real and imaginary parts), and [][] H H E E xx xx . Thus the original channel defined in (8.1) is equivalent to the channel y Λx n (8.10) where 1 2 , ,., ,0,.,0 m Λ diag with , 1,2,., i i m denoting the non-zero singular values of H. The equivalence is summarized in Fig. 8.2. From (8.10), we obtain for the received signal components , 1 , m+1 i ii i i i y x n im y n iM (8.11) It is seen that received components , i y i m , do not depend on the transmitted signal. On the other hand, received components , 1,2,., i y i m depend only the transmitted component i x . Thus the equivalent MIMO channel in (8.10) can be considered as consisting of m uncoupled parallel Gaussian sub-channels. Specifically, If N>M, (8.11) indicates that there will be at most M non-zero attenuation subchannels in the equivalent MIMO channel. See Fig. 8.3. If M>N, there will be at most N non-zero attenuation subchannels in the equivalent MIMO channel
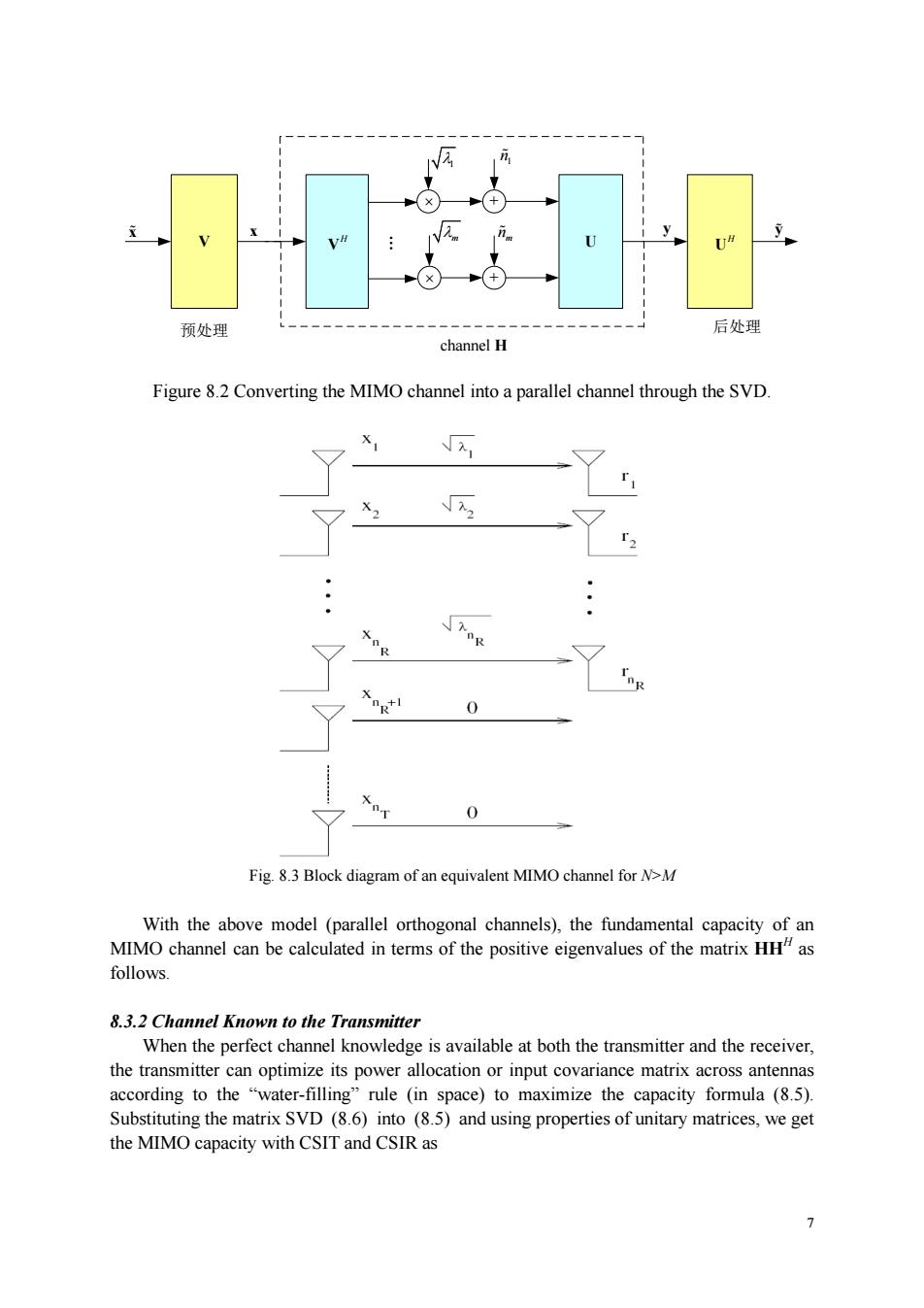
日 channel H Figure 8.2 Converting the MIMO channel into a parallel channel through the SVD. X r Xog'I 0 0 Fig.8.3 Block diagram of an equivalent MIMO channel for N>M With the above model (parallel orthogonal channels),the fundamental capacity of an MIMO channel can be cale ated in terms of the positive eigenvalues of the matrix HHas follows 8.3.2 Channel Known to the Transmitter When the perfect channel knowledge is available at both the transmitter and the receiver, the transmitter according to the Substituting the matrix SVD (8.6)into (8.5)and using properties of unitary matrices,we get the MIMO capacity with CSIT and CSIR as 7
7 V U x H V . + + H U 1 m 1 n mn y 预处理 后处理 channel H x y Figure 8.2 Converting the MIMO channel into a parallel channel through the SVD. Fig. 8.3 Block diagram of an equivalent MIMO channel for N>M With the above model (parallel orthogonal channels), the fundamental capacity of an MIMO channel can be calculated in terms of the positive eigenvalues of the matrix HHH as follows. 8.3.2 Channel Known to the Transmitter When the perfect channel knowledge is available at both the transmitter and the receiver, the transmitter can optimize its power allocation or input covariance matrix across antennas according to the “water-filling” rule (in space) to maximize the capacity formula (8.5). Substituting the matrix SVD (8.6) into (8.5) and using properties of unitary matrices, we get the MIMO capacity with CSIT and CSIR as

C=ea+元K,刃》 =路2e1+光) whereP is the transmit power in the th sub-channel.Solving the optimiation leads toa water-filling power allocation over the parallel channels.The power allocated to channel i. 1sism,is given parametrically by (8.12) where adenotes mx(a),and uis a constant that is chosen to satisfy En-p (8.13) The resulting capacity is then C.og.()oe. bits/channel use (8.14) which is achieved by choosing each component according to an independent Gaussian K,=VPV where P=diag(P.B.0)is an NxN matrix.Figure 8.4 depicts the SVD-based architechture for MIMO communication. coder Figure 8.4 The SVD-based architechture for MIMO communication Water-filling algorithm: The power allocation in (8.12)can be determined iteratively using the water-filling
8 2 :( ) 0 1 max log det x x H N x Tr P C N I Λ Λ K K K 2 : 1 0 max log 1 i i i m i i P PP i P N where Pi is the transmit power in the ith sub-channel. Solving the optimization leads to a water-filling power allocation over the parallel channels. The power allocated to channel i, 1im, is given parametrically by 0 i i N P (8.12) where a+ denotes max(0, a), and is a constant that is chosen to satisfy 1 m i i P P (8.13) The resulting capacity is then WF 2 0 2 1 1 0 0 1 1 log 1 log m m i i i i C N N N bits/channel use (8.14) which is achieved by choosing each component i x according to an independent Gaussian distribution with power Pi. The covariance matrix of the capacity-achieving transmitted signal is given by H Kx VPV where 1 2 diag , ,., ,0,.,0 P PP Pm is an NN matrix. Figure 8.4 depicts the SVD-based architechture for MIMO communication. V + AWGN coder AWGN coder H Decoder Decoder H U um u1 1 x m x . . . 1 y m y n 0 0 Figure 8.4 The SVD-based architechture for MIMO communication. Water-filling algorithm: The power allocation in (8.12) can be determined iteratively using the water-filling

algorithm.We now describe it. We first set the iteration count p to1 and assume that所有(m-p+l)个并行子信道都使 .With this assumption,the constant is calculated(by substituting(8.12)into (8.13))as -》 Then we have n-pp空别 (8.15a) Using this value of the power allocated to the ith subchannel is given by -(-艾)-12m-pl (8.15b) If the power allocated to the channel with the lowest gain is negative(i.e.,P<). then we discard this channel by setting P=0 and return the algorithm with the iteration count p=p叶1.即迭代执行(8.15a)和(8.15b),将总功率P在剩余的(m-pr1)个子信道之间 进行分配。迭代计算直到获得的所有P≥0或一m为止。 8.3.3Ch nel Unknown to the Transmitter If the channel is known to the receiver,but not to the transmitter,then the transmitter cannot optimize its power allocation or input covariance structure across antennas.This implies that if the distribution of H follows the zero-mean spatially white(ZMSW)channel gain model,the signals transmitted from N antennas should be independent and the power should be equally divided among the transmit antennas,resulting an input covariance matrix Thus,the capacity in such a case is eaL.+sRmr)tw<N C={ bits per channel use (8.15) ea,+sNum小fw≥N where SNR=P/N.Using the SVD of H,we can express this as c-2e+-2+)
9 algorithm. We now describe it. We first set the iteration count p to 1 and assume that 所有(m-p+1)个并行子信道都使 用。With this assumption, the constant is calculated (by substituting (8.12) into (8.13)) as 1 0 1 m p i i N P Then we have 1 0 1 1 1 1 m p i i P N m p (8.15a) Using this value of , the power allocated to the ith subchannel is given by 0 , 1,2,., 1 i i N P i mp (8.15b) If the power allocated to the channel with the lowest gain is negative (i.e., 1 0 P m p ), then we discard this channel by setting 1 0 P m p and return the algorithm with the iteration count p = p+1. 即迭代执行(8.15a)和(8.15b),将总功率 P 在剩余的(m-p+1)个子信道之间 进行分配。迭代计算直到获得的所有 0 Pi 或 p=m 为止。 8.3.3 Channel Unknown to the Transmitter If the channel is known to the receiver, but not to the transmitter, then the transmitter cannot optimize its power allocation or input covariance structure across antennas. This implies that if the distribution of H follows the zero-mean spatially white (ZMSW) channel gain model, the signals transmitted from N antennas should be independent and the power should be equally divided among the transmit antennas, resulting an input covariance matrix x N P N K I . It is shown in [Telatar99] that this Kx indeed maximize the mutual information. Thus, the capacity in such a case is 2 2 log det , if log det , if H M H N M N N C M N N I HH I HH SNR SNR bits per channel use (8.15) where 0 SNR P N/ . Using the SVD of H, we can express this as 2 1 0 log 1 m ri i P C N 2 1 0 log 1 m i i P NN

-交e刘 bits/channel use (8.16) where Pn is the received signal power in the ith sub-channel.Equation (8.16)expresses the capacity of the MIMO channel as a sum of the capacities of m SISO channels,each having a power gain ofand transmit power P/N.(Note:Because of the use of complex signals,the above unit is sometimes expressed in terms of"bits/sec/Hz") Since the nonzero eigenvalues of HH"are the same as those of HH,the capacity of a channel with matrix H and H are the same.Furthermore,the capacity can be achieved by choosing independent1sism with each having independent Gaussian,zero-mean real and imaginary parts. 8.3.4 MIMO Capacity Examples Example I [Single antenna channel].Consider a channel with N=M=1 and H=h=1.The Shannon capacity of this channel is C=log:1+P =log2(1+y1h) bit/channel use (8.17) Example 2 [MIMO channel with coherent combining].Consider a MIMO channel withh=1 for all IsisN,IsjsM.We can write Has 「/M H=UDV#= (MN)[/N./N 1/M and we see that the diagonal matrix D will have only one nonzero entry M.Thus,the Shannon capacity of this channel is c-w别 (8.18) The x=V that achieves this capacity satisfies E[x]=P/N for all i.j.i.e.,the transmitters are all sending the same signal.Thus,we can see that H corresponds to such a system in which the same signal x is transmitted from N transmit antennas and the receiver performs coherent maximum ratio combining (MRC)by M antennas.Then (8.18)can be interpreted as follows The received signal at antenna i is given by y=Nx and the received signal power at P antenna i is P.=N2 Since each receiver sees the same signal,and the noises at the
10 2 1 log 1 m i i N SNR bits/channel use (8.16) where Pri is the received signal power in the ith sub-channel. Equation (8.16) expresses the capacity of the MIMO channel as a sum of the capacities of m SISO channels, each having a power gain of i and transmit power P/N. (Note: Because of the use of complex signals, the above unit is sometimes expressed in terms of “bits/sec/Hz”.) Since the nonzero eigenvalues of HHH are the same as those of HHH, the capacity of a channel with matrix H and HH are the same. Furthermore, the capacity can be achieved by choosing independent { ,1 } i x i m with each i x having independent Gaussian, zero-mean real and imaginary parts. 8.3.4 MIMO Capacity Examples Example 1 [Single antenna channel]. Consider a channel with N=M=1 and H=h=1. The Shannon capacity of this channel is 2 2 2 2 0 | | log 1 log 1 | | P h C h N bit/channel use (8.17) Example 2 [MIMO channel with coherent combining]. Consider a MIMO channel with hij=1 for all 1iN, 1jM. We can write H as 1/ 1/ 1/ 1/ H M MNN N M H UDV and we see that the diagonal matrix D will have only one nonzero entry MN . Thus, the Shannon capacity of this channel is 2 0 log 1 P C MN N (8.18) The x Vx that achieves this capacity satisfies * [] / E i j xx P N for all i, j; i.e., the transmitters are all sending the same signal. Thus, we can see that H corresponds to such a system in which the same signal x is transmitted from N transmit antennas and the receiver performs coherent maximum ratio combining (MRC) by M antennas. Then (8.18) can be interpreted as follows. The received signal at antenna i is given by i y Nx and the received signal power at antenna i is 2 ri P P N N . Since each receiver sees the same signal, and the noises at the