
0122229现代数字通信与编码理论 September 1,2022 XDU,Fall 2022 Lecture Notes Chapter 2 Modulation and Coding for Ideal Gaussian channels This chapter is devoted to the discussion on orthonormal PAM/QAM systems,capacity calculations for ideal AWGN channels,and the performance evaluation of small signa constellations Note:Some of material presented in this chapter is based on Forney's lecture notes. 2.1 Data modulation and Demodulation In data modulation we c onvert information bits into waveforms that are suitable for transmission over a communication channel. This is done,in general,by splitting data modulation(or channel encoding)into separate layers:mapping from a sequence of binary digits into a sequence of real or complex numbers (numerical signals),followed by the conversion of signals to a waveform.Demodulation is the corresponding process at the ece maps the received waveform to a sequence of received signals In a passband system,modulators usually include a third layer,which maps a baseband-encoded waveform()into a passband wavefor(( with carrier frequencyf.At the receiver this passband waveform is mapped back to aseband ning the other components of decoding.This frequency conversion operation at encoder and decoder is often referred to as modulation and demodulation,but it is more common today to use the word modulation for the entire process of mapping bits to waveforms.Figure 2.0 illustrates these three layers. Binary Bits to Signals to Baseband to Input signals waveform passband of baseband pas an Channel waveform Binary Signal Waveform Passband to Output decoder to signals baseband Figure 2.0 The layers of a modulator (channel encoder)and demodulator (channel decoder) 2.1.1 Mapping of vectors to waveform It is well-known that any continuous-time function x()C defined on the interval [0. T]can be decomposed according to some set of N orthonormal basis function (t),Isks 2-1
2-1 0122229 现代数字通信与编码理论 September 1, 2022 XDU, Fall 2022 Lecture Notes Chapter 2 Modulation and Coding for Ideal Gaussian channels This chapter is devoted to the discussion on orthonormal PAM/QAM systems, capacity calculations for ideal AWGN channels, and the performance evaluation of small signal constellations. Note: Some of material presented in this chapter is based on Forney’s lecture notes. 2.1 Data Modulation and Demodulation In data modulation we convert information bits into waveforms that are suitable for transmission over a communication channel. This is done, in general, by splitting data modulation (or channel encoding) into separate layers: mapping from a sequence of binary digits into a sequence of real or complex numbers (numerical signals), followed by the conversion of signals to a waveform. Demodulation is the corresponding process at the receiver. The demodulator maps the received waveform to a sequence of received signals, which is then mapped to a bit sequence. In a passband system, modulators usually include a third layer, which maps a baseband-encoded waveform () b x t into a passband waveform 2 ( ) 2 ( ) c j f t b x t x t e = R with carrier frequency fc. At the receiver this passband waveform is mapped back to baseband before performing the other components of decoding. This frequency conversion operation at encoder and decoder is often referred to as modulation and demodulation, but it is more common today to use the word modulation for the entire process of mapping bits to waveforms. Figure 2.0 illustrates these three layers. Figure 2.0 The layers of a modulator (channel encoder) and demodulator (channel decoder) 2.1.1 Mapping of vectors to waveform It is well-known that any continuous-time function 2 x t( ) defined on the interval [0, T] can be decomposed according to some set of N orthonormal basis function {k(t), 1 k

N)as 0-2400s1s7 2.10 Relationship in (2.1)indicates a correspondence between an N-dim real-valued vector x=[x.xxER and the waveformx(r)eC.Let x be a data symbol.Then the modulated signal(waveform)corresponding tox is given by (2.1). (t) ● ON() ● N Figure Modulator the basis expansion. Similarly,a set of continuous-time function()corresponds to a set of discrete N-dim pointsx known as a signal constellation. ous-time functions can be extended to random processes using what is known as Karhunen-Loeve expansion.Decomposition of random processes is fundamental to demodulation and detection in the presence of noise.Modulation constructively assembles random signals for the communication system from a set of basis functions())and a set of signal pointsx 2.1.2 Demodulation The demodulation takes the continuous-time waveforms and extracts the received version.Given the basis expansion of(2.1),the demodulation extracts the coefficients of the expansion by projecting the(received)signal onto its basis as shown below. 00t=2A0e0a =立x0404.0d =26= (22) Therefore in the noiseless case,demodulation is just recovering the coefficients of the 3
2-2 N} as 1 ( ) ( ) N k k k x t x t = = , 0 t T (2.1) Relationship in (2.1) indicates a correspondence between an N-dim real-valued vector 1 T N N x = x x and the waveform 2 x t( ) . Let x be a data symbol. Then the modulated signal (waveform) corresponding to x is given by (2.1). Figure 2.1 Modulator implements the basis expansion. Similarly, a set of continuous-time function x t i ( ) corresponds to a set of discrete N-dim points xi known as a signal constellation. This decomposition of continuous-time functions can be extended to random processes using what is known as Karhunen-Loeve expansion. Decomposition of random processes is fundamental to demodulation and detection in the presence of noise. Modulation constructively assembles random signals for the communication system from a set of basis functions {k(t)} and a set of signal points xi . 2.1.2 Demodulation The demodulation takes the continuous-time waveforms and extracts the received version. Given the basis expansion of (2.1), the demodulation extracts the coefficients of the expansion by projecting the (received) signal onto its basis as shown below. 0 0 1 ( ) ( ) ( ) ( ) N T T n k k n k x t t dt x t t dt = = 0 1 ( ) ( ) N T k k n k x t t dt = = 1 N k kn n k x x = = = (2.2) Therefore in the noiseless case, demodulation is just recovering the coefficients of the
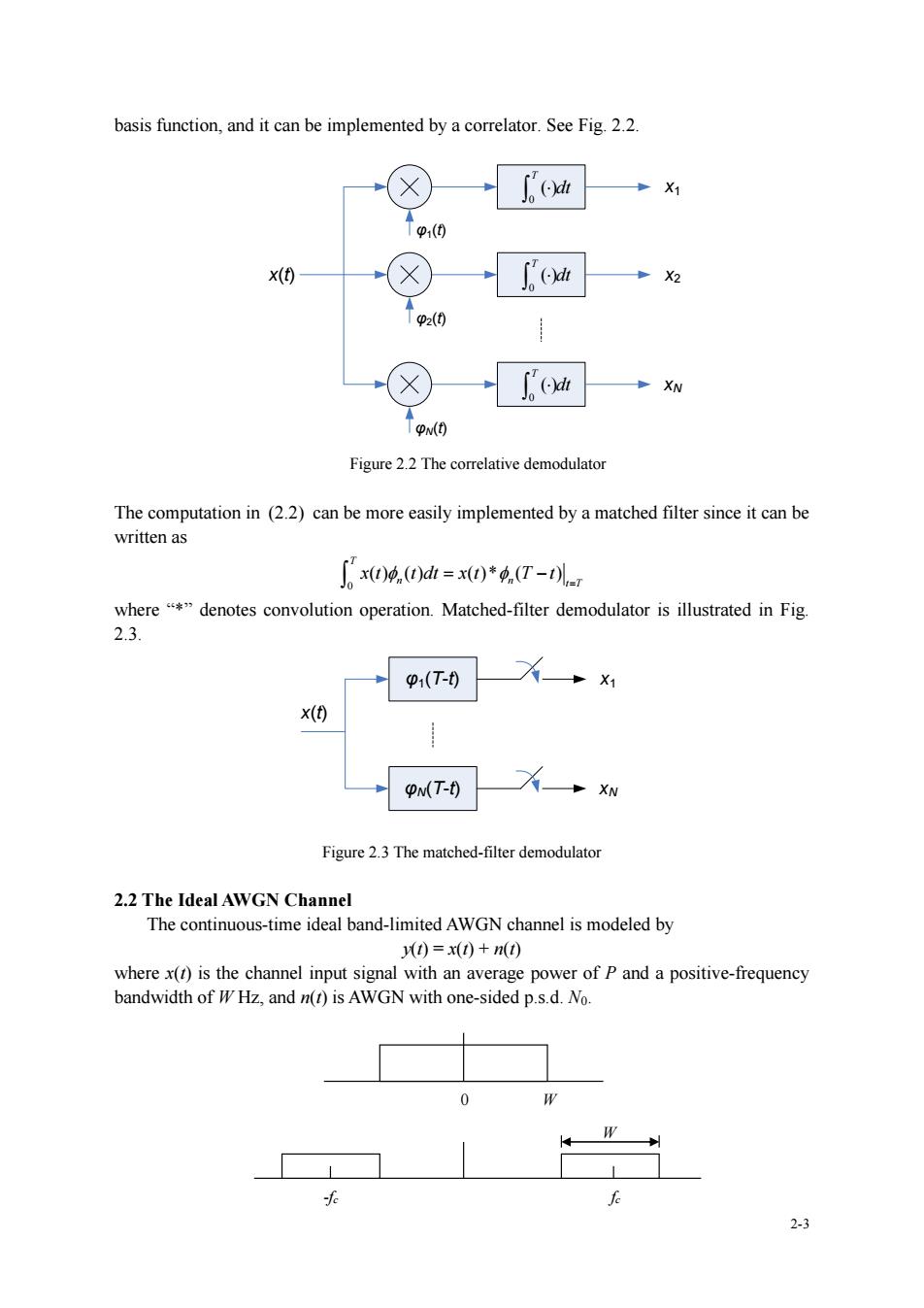
basis function,and it can be implemented by a correlator.See Fig.2.2. Tp1(0 x(t) fo Tp2(0 ox ↑p Figure 2.2 The correlative demodulator The computation in (2.2)can be more easily implemented by a matched filter since it can be a x0.0dh=xo)*.(T-儿 where"*"denotes convolution operation.Matched-filter demodulator is illustrated in Fig. 2.3. p1(T-0 pMT-用 Figure 2.3 The matched-filter demodulator 2.2 The Ideal AWGN Channel The continuous-time ideal band-limited AWGN channel is modeled by 0=x(0+n0 where()is the channel input signal with an average power of P and a positive-frequency bandwidth of W Hz,and n(t)is AWGN with one-sided p.s.d.No. 0
2-3 basis function, and it can be implemented by a correlator. See Fig. 2.2. 0 () T dt 0 () T dt 0 () T dt x1 x2 xN φ1(t) φ2(t) φN(t) x(t) Figure 2.2 The correlative demodulator The computation in (2.2) can be more easily implemented by a matched filter since it can be written as 0 ( ) ( ) ( )* ( ) T n n t T x t t dt x t T t = = − where “*” denotes convolution operation. Matched-filter demodulator is illustrated in Fig. 2.3. φ1(T-t) φN(T-t) x(t) x1 xN Figure 2.3 The matched-filter demodulator 2.2 The Ideal AWGN Channel The continuous-time ideal band-limited AWGN channel is modeled by y(t) = x(t) + n(t) where x(t) is the channel input signal with an average power of P and a positive-frequency bandwidth of W Hz, and n(t) is AWGN with one-sided p.s.d. N0. 0 W fc W -fc

Figure 2.4 Ideal band-limited channel with bandwidth The channel band B is a positive-frequency interval with bandwidth W Hz.The channel is said to be baseband if B=[0,]and passband otherwise. 2.1.1 Conversion from the continous-time AWGN channel into a vector channel Lett),1sksN)denote a set of real orthonormal waveforms.Then the transmitted signal can be expressed as x(0=∑x4,0,0≤1≤T (2.1) With optimal receiver,the sampled output of the matched-filter(MF)demodulator is given by =(0),40》=∫y)40)d=x+n (2.2) where yis a set of sufficient statistics about(d (dr is a set of idreal Gaussian random variables with zero mean and variance =No/2 Equation (2.2)is the discrete-time ideal AWGN channel model.Notice that there is no intersymbol interference(ISI). 2.3 Signal Constellations An N-dimensional signal constellation (signal set.alphabet)of size M is a set A=ajsM)of Mreal N-tuples aR.Each distinct point(called signal point)in the signal constellation corresponds to a different modulated waveform,but all the waveforms share the same set of basis functions.Such a set is able to transmit log,M bits per Ndimensions.Some examples of signal constellations are shown in Fig.2.5
2-4 Figure 2.4 Ideal band-limited channel with bandwidth W ⚫ The channel band B is a positive-frequency interval with bandwidth W Hz. The channel is said to be baseband if B = [0, W], and passband otherwise. 2.1.1 Conversion from the continuous-time AWGN channel into a vector channel Let {k(t), 1 k N} denote a set of real orthonormal waveforms. Then the transmitted signal can be expressed as 1 ( ) ( ) N k k k x t x t = = , 0 t T (2.1) With optimal receiver, the sampled output of the matched-filter (MF) demodulator is given by 0 ( ), ( ) ( ) ( ) T k k k k k y y t t y t t dt x n = = = + (2.2) where ⚫ {yk} is a set of sufficient statistics about 0 ( ) ( ) T k k x x t t dt = ; ⚫ 0 ( ) ( ) T k k n n t t dt = is a set of i.i.d. real Gaussian random variables with zero mean and variance 2 0 /2 n = N . Equation (2.2) is the discrete-time ideal AWGN channel model. Notice that there is no intersymbol interference (ISI). 2.3 Signal Constellations An N-dimensional signal constellation (signal set, alphabet) of size M is a set { ,1 } j = a j M of M real N-tuples N a j . Each distinct point (called signal point) in the signal constellation corresponds to a different modulated waveform, but all the waveforms share the same set of basis functions. Such a set is able to transmit 2 log M bits per N dimensions. Some examples of signal constellations are shown in Fig. 2.5

M1,M2 2,M4 W3,M=8 Figure 2.5(a)Cubic constellations for N=1,2 and 3. ●】 ● Figure 2.5(b)A circular constellation The average energy ofA(per N dimensions)is defined by E、=eIa,]-2Ia,rPmU) (2.3) where Pr()is the probability of choosinga EN is closely related to the average power P by P=E/T with Tstanding for the signal duration(symbol interval). The minimum distance between constellation points is denoted by dn(A)=min‖a,-a, (2.4) which is related to the probability of error of detector. The above power constraints and minimum distance constitutes two key parameters of a signal constellation.Other parameters are as follows. .A system with symbol interval T and bandwidth W has a number of dimensions avail ble N=2WT The average number of bits per dimension is b=log:M bits/dim 3
2-5 N=1, M=2 N=2, M=4 N=3, M=8 Figure 2.5 (a) Cubic constellations for N=1, 2 and 3. Figure 2.5 (b) A circular constellation The average energy of (per N dimensions) is defined by 2 2 1 || || || || Pr( ) M N j j j E j = = = E a a (2.3) where Pr(j) is the probability of choosing aj. EN is closely related to the average power P by P = EN / T with T standing for the signal duration (symbol interval). The minimum distance between constellation points is denoted by min ( ) min || || i j i j d = − a a , (2.4) which is related to the probability of error of detector. The above power constraints and minimum distance constitutes two key parameters of a signal constellation. Other parameters are as follows. ⚫ A system with symbol interval T and bandwidth W has a number of dimensions available for constellation construction N = 2WT ⚫ The average number of bits per dimension is 2 log M b N = bits / dim

.The data rate is R=log,M/T bits/s. Then 2b=R/W=p,which is the spectral efficiency of a modulation scheme(bits s/Hz).or p=是1g,M bits/2D The average energy of A per dimension is given by E=E/N If the Msignal points inA are assumed to be equiprobable,then f 2,fm2 To simplify performance assessment,we define a figure of merit (CFM)for a constellation as 5e山 (2.5) As we have stated in Chapter 1,from the signal space viewpoint,the data modulation can be viewed as a two-step process:a signal mapper followed by a simple waveform converter.A signal mapper performs the mapping of a binary vector of length logM into one of a const thethe siaon Mapping is not airary.clever shoices Iead to betcr lation ally,the binar vector performance over noisy channels. In some channels it is suitable to label points that are close in Euclidean distance to map to being close in Hamming distance.An example for such mapping is the Gray-mapping Fig 2.6 illustrates an example. 1
2-6 ⚫ The data rate is 2 R M T = log / bits/s. ⚫ Then 2 / b R W = , which is the spectral efficiency of a modulation scheme (bits / s / Hz), or 2 2 log M N = bits / 2D ⚫ The average energy of per dimension is given by Ed = EN / N If the M signal points in are assumed to be equiprobable, then 2 1 1 || || M N j j E M = = a and 2 1 1 || || M d j j E MN = = a ⚫ To simplify performance assessment, we define a figure of merit (CFM) for a constellation as 2 min ( ) 4 d d E (2.5) As we have stated in Chapter 1, from the signal space viewpoint, the data modulation can be viewed as a two-step process: a signal mapper followed by a simple waveform converter. A signal mapper performs the mapping of a binary vector of length log2M into one of the signal points in a constellation of size M. Usually, the binary vector is referred to as the label of the signal point. Mapping is not arbitrary, clever choices lead to better performance over noisy channels. In some channels it is suitable to label points that are close in Euclidean distance to map to being close in Hamming distance. An example for such mapping is the Gray-mapping. Fig. 2.6 illustrates an example

8-PSK 16-QAM ↑m ←lm 011● ●001 01i101i00010o0i1 010● ●000 Re 0101010000000001. 110● ●100 1101110010o01o07Re 111● ●101 111110101010g1 Figure 26 Gray-coded mapper for QPSK.8-PSK.and 16-QAM constellations.Neighboring symbols differ in only one bit. Denote the jth signal vector in A by a,=(a).Then the selected signal is a set of N orthonormal waveforms.This provides a general scenario for mapping the symbols I to M into a set of signal waveforms b(r)to b().If we transmit a sequence of such M-ary symbols at T-spaced symbol-intervals,the most straightforward way of accomplishing this is to choose the orthonormal waveforms).(t)in such a way that-T)and (-/'T)are orthonormal for all k,m,Isk,m<N,and all integers Note that PAM is a special case of this scenario where the dimension N=1,and the function)is the real modulation pulse p(r)for baseband transmission:QAM is another special case where N=2 at passband.In this case,the complex signals a are viewed as 2D real signals.The orthonormal waveforms (assuming real p())are)=2p()cos(2) and()=2p(r)sin(f).See the following for a brief discussion.A more detailed discussion can be found in [Gallgar,200] 2.4 Orthonormal PAM/QAM Systems We now proceed to consider the modulation system with PAM/QAM signaling.The system block model is depicted in Fig.2.7.together with the notation to be used in the 2
2-7 Figure 2.6 Gray-coded mapper for QPSK, 8-PSK, and 16-QAM constellations. Neighboring symbols differ in only one bit. Denote the jth signal vector in by ,1 ,2 , ( , ,., ) j j j j N a = a a a . Then the selected signal vector j a is modulated into a signal waveform , 1 ( ) ( ) N j j k k k b t a t = = , where 1 ( ),., ( ) t t N is a set of N orthonormal waveforms. This provides a general scenario for mapping the symbols 1 to M into a set of signal waveforms 1 ( ) to ( ) M b t b t . If we transmit a sequence of such M-ary symbols at T-spaced symbol-intervals, the most straightforward way of accomplishing this is to choose the orthonormal waveforms 1 ( ),., ( ) N t t in such a way that ( ) and ( ) k m t lT t l T − − are orthonormal for all k m k m N , ,1 , , and all integers ll, . Note that PAM is a special case of this scenario where the dimension N = 1, and the function 1 ()t is the real modulation pulse p(t) for baseband transmission; QAM is another special case where N = 2 at passband. In this case, the complex signals aj are viewed as 2D real signals. The orthonormal waveforms (assuming real p(t)) are 1 ( ) 2 ( )cos(2 ) c t p t f t = and 2 ( ) 2 ( )sin(2 ) c t p t f t = . See the following for a brief discussion. A more detailed discussion can be found in [Gallgar, 2008]. 2.4 Orthonormal PAM / QAM Systems We now proceed to consider the modulation system with PAM/QAM signaling. The system block model is depicted in Fig. 2.7, together with the notation to be used in the

following discussions. Baseband modulation Baseband topassband -Encoder Signal Pulse x(t) Up- s(t) mapper shaping conversion P(O and democ ulation Passband to baseban Decoder etector y Matched yt) Down- conversion 90 Figure 2.7 Block model of modulation and demodulation 2.4.1 Orthonormal PAM ■PAM Signal Set A standard M-PAM signal set A consists of M=A]=2d-spaced real numbers located symmetrically about the origin;i.e., A={-d(M-1)/2,-d/2,d/2,d(M-l0/2} where bis the number of bits transmitted per symbol.See the figure below Assume that the signal points are equiprobable.Then the average energy per symbol 不-小心-音山g- (2.6) 12 For example,for M.4 and/4.5d/4 and /,respectively. An alternative derivation 思考题:Let Ube a random variable uniformly distributed in-d,and letbe adiscrete random variable independent of Uand uniformly distributed over the PAM constellationd, +3d,.,(m-1)d),where m is an even integer.Let V=+U. (a)Find the distribution of 2-8
2-8 following discussions. Encoder Signal mapper Pulse shaping Up- conversion uk ck xk x(t) Baseband modulation Baseband to passband s(t) Channel Down- conversion Passband to baseband Matched filter Decoder Detector y(t) r(t) Sample at t=kT yk Baseband demodulation p(t) q(t) ˆ k u Figure 2.7 Block model of modulation and demodulation 2.4.1 Orthonormal PAM ◼ PAM Signal Set A standard M-PAM signal set consists of M = || = 2b d-spaced real numbers located symmetrically about the origin; i.e., = − − − − { ( 1) / 2,., / 2, / 2,., ( 1) / 2} d M d d d M where b is the number of bits transmitted per symbol. See the figure below. Assume that the signal points are equiprobable. Then the average energy per symbol is 2 2 2 / 2 / 2 2 2 / 2 / 2 1 ( 1) 12 dM d dM d a d M A a da da − − dM d − = − = (2.6) For example, for M = 2, 4 and 8, 2 2 2 2 A d d d = / 4,5 / 4 and 21 / 4 , respectively. An alternative derivation: 2 / 2 2 3 2 2 1 2 2 1 2 2 6 6 M i i d M M A d M M = − = = − 思考题: Let U be a random variable uniformly distributed in [−d, d] and let S be a discrete random variable independent of U and uniformly distributed over the PAM constellation {±d, ±3d, ., ±(m−1)d}, where m is an even integer. Let V = S + U. (a) Find the distribution of V

(b)Find the variance of Uand that of V. (e)Use pa (b)todetermine the varianc f(the average energy of thePAMwith uniform distribution.) ■PAM Modulator A PAM modulator converts a discrete-time sequencex kEZ of real symbols into a continuous-time real waveform x0=∑xP1-k灯) where T is the symbol interval,p(r)is the basic modulation pulse,and xA. A PAM system is said to be orthonormal if (p-kT),p-jT)》=d- that is)=ip(t-kT) With the assumption that the underlying channel model is an ideal AWGN channel. the received basebar d waveform is given by )=x0+0 In an orthonormal PAM system,the sequenceof matched-filter outputs is given by y=((I),p1-kT)》=x4+n we obtain without loss of optimality an cquivalent discrete-time GN channel y=x+n 2.4.2 Orthonormal OAM ■QAM Signal Set (MxM)-QAM signal set consists of the Cartesian product of two A=a=(a'+ja")la'EA'.a"EA') whereA'=(-d(M-1)/2.-d/2,d/2.d(M-1)/2).Thus the size of A is Al=M, and the number of bits per symbol is 2log2M=2b.See Fig.2.8 for examples.Assuming that the symbols in A are equiprobable,the average energy per complex symbol is F=2×dM-dM- 2 (2.7) 2.9
2-9 (b) Find the variance of U and that of V . (c) Use part (b) to determine the variance of S. (i.e., the average energy of the PAM with uniform distribution.) ◼ PAM Modulator A PAM modulator converts a discrete-time sequence {xk, k} of real symbols into a continuous-time real waveform ( ) ( ) k k x t x p t kT = − where T is the symbol interval, p(t) is the basic modulation pulse, and xk . A PAM system is said to be orthonormal if ( ), ( ) k j p t kT p t jT − − = − that is {k(t)} = {p(t-kT)}. With the assumption that the underlying channel model is an ideal AWGN channel, the received baseband waveform is given by y(t) = x(t) + n(t) In an orthonormal PAM system, the sequence {yk} of matched-filter outputs is given by ( ), ( ) k k k y y t p t kT x n = − = + Thus, we obtain without loss of optimality an equivalent discrete-time AWGN channel model y = x + n 2.4.2 Orthonormal QAM ◼ QAM Signal Set A standard (MM)-QAM signal set consists of the Cartesian product of two standard M-PAM d-spaced signal set; i.e., = = + a a ja a a ( ' '') | ' , '' ' ' where ' = − − − − { ( 1) / 2,., / 2, / 2,., ( 1) / 2} d M d d d M . Thus the size of is || = M2 , and the number of bits per symbol is 2log2M = 2b. See Fig. 2.8 for examples. Assuming that the symbols in are equiprobable, the average energy per complex symbol is 2 2 2 2 2 ( 1) ( 1) 2 12 6 d M d M A − − = = (2.7)

4-QAM Figure 2.8 QAM constellations ■QAM Modulator A QAM baseband modulator converts a discrete-time sequence kZof complex symbols into a continuous-time complex waveform x()=∑P-kT) where T is the symbol interval,p(t)is the complex modulation pulse,and xAcC. From the impementa tion viewpoint,it is helpful to view the modulation in terms of filtering,see Fig.2.9.If p()is real,this corresponds to two real filtering operations. znak009 Figure 2.9 AQAM system is said to be orthonormal if (pu-kT),p1-jT))=6- where the inner product is defined as (().g()=f()g'(d In a passband QAM system,x(r)is then up-modulated to passband.After 2-10
2-10 1 2 16-QAM 4-QAM 2 d 2 d − Figure 2.8 QAM constellations ◼ QAM Modulator A QAM baseband modulator converts a discrete-time sequence {xk, k} of complex symbols into a continuous-time complex waveform ( ) ( ) k k x t x p t kT = − where T is the symbol interval, p(t) is the complex modulation pulse, and xk . From the implementation viewpoint, it is helpful to view the modulation in terms of filtering, see Fig. 2.9. If p(t) is real, this corresponds to two real filtering operations. Figure 2.9 A QAM system is said to be orthonormal if ( ), ( ) k j p t kT p t jT − − = − where the inner product is defined as * f t g t f t g t dt ( ), ( ) ( ) ( ) = . In a passband QAM system, x(t) is then up-modulated to passband. After p(t) x(t) xk(t-kT)