
State Key Laboratory of Integrated Services Networks 国家重点实验室 Polar Codes 西安电子科技大学SN 白宝明 2017.11.13
State Key Laboratory of Integrated Services Networks Polar Codes 西安电子科技大学ISN 白宝明 2017.11.13

N 国家重点实验室 Outline o Introduction o Channel Polarization o Construction Encoding Decoding o Performance o Open Problems 2
Outline Introduction Channel Polarization Construction Encoding & Decoding Performance Open Problems 2

国家重点实验室 Introduction Polar codes,invented by Erdal Arikan in 2008, are the first codes to provably achieve capacity 。特点: >Capacity-achieving for symmetric binary-input memoryless channels(包括Bl-AWGN,BSC,BEC) >Low encoding and decoding complexity:O(Nlog N) >Block error probability is roughly O(2-N) And this performance guarantee is analytical. >For symmetric channels,code construction is deterministic. That is,the above statements are true not only for ensembles of codes,but also for individual polar codes
Introduction Polar codes, invented by Erdal Arikan in 2008, are the first codes to provably achieve capacity. 特点: Capacity-achieving for symmetric binary-input memoryless channels (包括BI-AWGN, BSC, BEC) Low encoding and decoding complexity: Block error probability is roughly And this performance guarantee is analytical. For symmetric channels, code construction is deterministic. That is, the above statements are true not only for ensembles of codes, but also for individual polar codes. 3 ON N ( log ) (2 ) N O −

国家重点实验室 核心思想 o Channel Polarization >Create extreme channels:Either noiseless or useless. o Channel coding problem trivial for these two types of channels >Perfect channels:C(W)=1,the output Y determines the input X Useless channels:C(W)=0,the output Y is independent of the input X o Channel polarization is a technique to convert any binary-input channel into a mixture of binary-input extreme channels 。极化方法 >信道合并与分裂(由编译码共同完成) 4
核心思想 Channel Polarization Create extreme channels: Either noiseless or useless. Channel coding problem trivial for these two types of channels Perfect channels: C(W)=1, the output Y determines the input X Useless channels: C(W)=0, the output Y is independent of the input X Channel polarization is a technique to convert any binary-input channel into a mixture of binary-input extreme channels 极化方法 信道合并与分裂(由编译码共同完成) 4

N The Channel 国家重点实验室 Let w:be a binary-input discrete-memoryless channel X W >Input alphabet:=0,1 >Transition probabilities:W(ylx),x∈X,y∈y o Two independent uses of the channel W xi>w →Y xw→g Nindependent copies of W:WN:XN->YN w')=IIwG,I) 5
The Channel Let be a binary-input discrete-memoryless channel Input alphabet: Transition probabilities: , , Two independent uses of the channel W N independent copies of W: 5 X1 Y1 X2 Y2 W W W : → ={0,1} Wyx ( ) | x∈ y ∈ : NN N WX Y → 1 1 1 ( | ) (|) N N N N i i i W y x Wy x = =∏

国家重点实验室 Symmetry assumption and Capacity o Assume that the channel has "input-output symmetry. (Example:BSC,BEC) BEC(c) 0 1-9 0 (Symmetric)Capacity 1 1-c For channels with I/O symmetry,the capacity is given by C(W)≌I(X;Y) with X unif.(0,1) =∑∑)W0y川x)log W(yx) eeX2 W(y川0)+,W0y1D) 2 Use base-2 logarithms: 0≤C(W)≤1 6
Symmetry assumption and Capacity Assume that the channel has “input-output symmetry.” (Example: BSC, BEC) (Symmetric) Capacity For channels with I/O symmetry, the capacity is given by Use base-2 logarithms: 6 ( ) ( ; ) with unif. {0,1} 1 (|) ( | )log 2 1 1 ( | 0) ( |1) 2 2 y Yx X CW I X Y X Wyx Wyx W y W y ∈ ∈ = + 0 ()1 ≤ ≤ C W

国家重点实验室 Symmetry assumption and Capacity o Bhattacharyya parameter Z(wW)兰∑√W(y10)w(y1西 o The parameters C(W)and Z(W)are used as measures of rate and reliability. Define the decision region for message m,D=yAIf(y)=m For codes with two codewords,the error probability,when message 2 is transmitted,is P.(eI2)=∑Pw(ylx2) yeD For yeD1,Py(ylx)P(ylx2)for ML decoding 。经过简单处理,有P.(2)≤∑VRyx)R) yeD 进而P,(em)≤∑VP(yIx)P(y) known as the Bhattacharyya bound on error probability 7
Symmetry assumption and Capacity Bhattacharyya parameter The parameters C(W) and Z(W) are used as measures of rate and reliability. Define the decision region for message m, For codes with two codewords, the error probability, when message 2 is transmitted, is 经过简单处理,有 进而 7 ( ) ( | 0) ( |1) y Y ZW W y W y ∈ { | () } N m Y =∈ = y y f m 1 2 ( | 2) ( | ) Pe P B N ∈ = y y x For y ∈ 1, for ML decoding 1 2 (| ) (| ) P P N N yx yx ≥ 1 1 2 ( | 2) ( | ) ( | ) Pe P P B NN ∈ ≤ y y x y x 1 2 ( | ) ( | ) ( | ) P em P P B NN ≤ y y x y x known as the Bhattacharyya bound on error probability

国家重点实验室 Main idea for channel polarization Channel coding problem trivial for two types of channels Perfect:C(W)=1 Useless:C(W)=0 Transform ordinary W into such extreme channels >Perfect channels:C(W)=1,the output Y determines the input X Useless channels:C(W)=0,the output Y is independent of the input X o Channel polarization is a technique to convert any binary-input channel into a mixture of binary-input extreme channels
Main idea for channel polarization Perfect channels: C(W)=1, the output Y determines the input X Useless channels: C(W)=0, the output Y is independent of the input X Channel polarization is a technique to convert any binary-input channel into a mixture of binary-input extreme channels 8
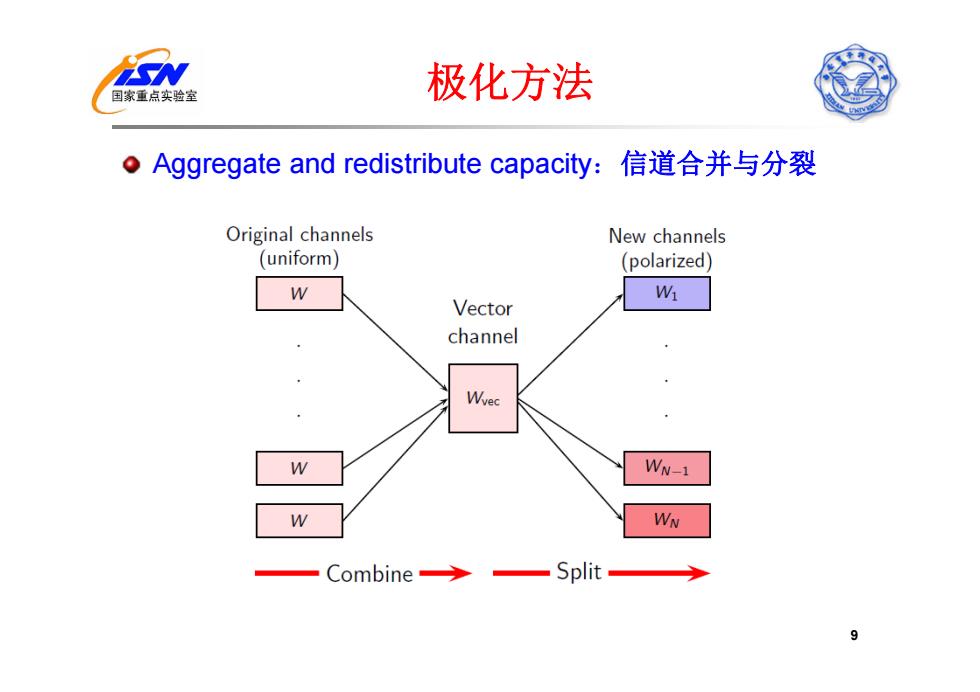
国家重点实验室 极化方法 。Aggregate and redistribute capacity:信道合并与分裂 Original channels New channels (uniform) (polarized) Wi Vector channel Wvec W WN-1 W WN Combine→ Split 9
极化方法 Aggregate and redistribute capacity:信道合并与分裂 9

国家重点实验室 Channel Combining 0 Begin with N copies of W >Use a 1-1 mapping Gw:{0,1W→{0,1} UNA IN-1 >to create a vector channel UN W:UN→YW oCombining operation is lossless: >Let U.Uv i.i.d.-Unif.01 then X,.Xy i.i.d.~Unif.(01) >and C(W)=I(UN;YN) =I(XN:YN) =NC(W) 10
Channel Combining Begin with N copies of W Use a 1-1 mapping to create a vector channel Combining operation is lossless: Let then and 10 :{0,1} {0,1 } N N GN → : N N WU Y N → 1,., i.i.d. Unif. {0,1} U UN 1,., i.i.d. Unif. {0,1} X X N () (;) ( ; ) ( ) N N N N N CW IU Y I X Y NC W = = =