
第一章绪论 本意主要内容: 2) (3)信息的度量 (4)通信系统的主要性能指标 本章重点: 1通信系统的一 般模型与数字通信系统模型 2。离敢信源的信息量 箱的计 3.数字通信系统的主要性能指标:码元传输速率与信息传输速率以及它们的关系、误码 率与误信率 本章练习题: 1-1. 解:e的信息量 1.=iog:p0-iog:2Pe)=-iog:0.105=325(6a x的信息量 0 1=ig:a-1g:2Pw)-iog,002=8976 1-2。某信源符号集由A,B,C,D和正组成,设每一符号独立出现,其出现藏率分别为么,冷, 发,为和名6。试求该信息源符号的平均信息量。 ·查看参考答案 解:平均信息量(嫡) H切=-2P)iag:Pa o8:os:86e6os:话 =223:/符于) 14.设有4个符号,其中前3个符号的出现版率分别为片,发,发,且各符号的出现是相 对独立的。试计算该符号集的平均信息量。 查看参考答案 解:各符号的相辟之和等于1,故第4个符号的率为为,则 该符号集的平均信息量为: H0子2×g:写50g:1.73符号) 1-4.一个由字母A、B、C、D组成的字,对于传输的每一个字母用二进制脉冲编码,00代替 A,01代替B,10代替C,11代替D,每个脉冲宽度为55. (1)不同的字母是等可能出现时,试计算传输的平均信息速率:
第一章 绪 论 本章主要内容: (1)通信系统的模型与基本概念 (2)通信技术的现状与发展 (3)信息的度量 (4)通信系统的主要性能指标 本章重点: 1.通信系统的一般模型与数字通信系统模型 2.离散信源的信息量、熵的计算 3.数字通信系统的主要性能指标:码元传输速率与信息传输速率以及它们的关系、误码 率与误信率 本章练习题: 1-1. 已知英文字母 出现的概率为 0.105, 出现的概念为 0.002,试求 和 的信息量。 • 查看参考答案 o 1-2.某信源符号集由 , , , 和 组成,设每一符号独立出现,其出现概率分别为 , , , 和 。试求该信息源符号的平均信息量。 • 查看参考答案 o 1-3. 设有 4 个符号,其中前 3 个符号的出现概率分别为 , , ,且各符号的出现是相 对独立的。试计算该符号集的平均信息量。 • 查看参考答案 o 1-4.一个由字母 、 、 、 组成的字,对于传输的每一个字母用二进制脉冲编码,00 代替 ,01 代替 ,10 代替 ,11 代替 ,每个脉冲宽度为 5 . (1)不同的字母是等可能出现时,试计算传输的平均信息速率;

(2)若每个字母出现的可能性分别为 品。品 试计算传输的平均信息速率 ·查看参考答案 解:(1)一个字母对应两个二进制码元,属于四进符号,故一 个字母的续时间(码元宽度)为2×5m,传输字母的号速率为 00() 等将时的平均信息速率 R.=R og:M=R log:4=200(bit s) (2)平均言息量为 H=-31og:2×宁og:1og:0=1985(符号) 非等拥时的平均信息速率为 RR-10x18518.50t 1-5.国际摩尔斯电码用“点”和“划”的序列发送英文字母,“划”用持续3单位的电流脉冲 表示,“点”用特续1个单位的电流冲表示:且“划”出现的概车是“点”出现概率的为。 (1)计算“点”和“划”的信息量: (2)计算“点”和“划”的平均信息量。 查看参考答案 解:(1)设点和成划出现的滓分别为2和?,三知P=2.=1, 故得P,P=,则点得信息量为 1=1og:万=-iog:=0415h 戈的信息量为 1-=og:广=-1og:=26词 (2)平均信息量为 0 H=x+xd_=0.3(符号) 16。设一信息源的输出由128个不同的符号组成。其中16个出现的概率为冷2,其余12个 出现概率为224。信息源每秒发出100个符号,且每个符号筱此独立。试计算该信息源的平 均信息速率。 ·查看参考答案
(2)若每个字母出现的可能性分别为 试计算传输的平均信息速率。 • 查看参考答案 o 1-5.国际摩尔斯电码用“点”和“划”的序列发送英文字母,“划”用持续 3 单位的电流脉冲 表示,“点”用持续 1 个单位的电流脉冲表示;且“划”出现的概率是“点”出现概率的 。 (1)计算“点”和“划”的信息量; (2)计算“点”和“划”的平均信息量。 • 查看参考答案 o 1-6.设一信息源的输出由 128 个不同的符号组成,其中 16 个出现的概率为 ,其余 112 个 出现概率为 。信息源每秒发出 1000 个符号,且每个符号彼此独立。试计算该信息源的平 均信息速率。 • 查看参考答案

解:每个符号的评均信息量 H=16×7:2+12×立g:24=6406符号) 已知符号速率元,=10008,故平均信息速率 ,-R:H-1000×6.4056405×10t) 1-7,设一数字传输系统传送二进制码元的速率为2400B,试求该系统的信息速率:若该系统改 送16进制信号码元,码元速 变,则这时的系统信息速率为多少(设各码元独立等概率出 现 ·查看参考答案 解:(1)二进时,RR:■2400t) (2)16进时,R=R,1s:16=2400x=6000it) 1-8.若1°2中信息源以100B速丰传送信息。 (1)试计算传送1h的信息量: (2)试计算传送1可能达到的最大信息量 。查看参考答案 解:(1由题1-2可知信息的牌 H=-之P1e:2Pa)=23h符号) 故平均信息速幸 R=RH=1000×223=223x10i 传送1的信息量 R,2.2310×3600-8.02810b 〔2)等时的信息烤大 H=10g5=233(抛符号) 此时平均信息速率最大,拉有最大信息量 1=R,H)-t-1000×2.23×3600=8.352×100i 1-9.如果二进制独立等概信号的码元宽度为0.5ms,求R。和R,若改为四进制信号,码元宽 度不变,求传码率R,和独立等概率时的传信率凡。 ·查看参考答案
o 1-7.设一数字传输系统传送二进制码元的速率为 2400 ,试求该系统的信息速率;若该系统改 为传送 16 进制信号码元,码元速率不变,则这时的系统信息速率为多少(设各码元独立等概率出 现)? • 查看参考答案 o 1-8.若题 1―2 中信息源以 1000 速率传送信息。 (1)试计算传送 1 的信息量; (2)试计算传送 1 可能达到的最大信息量。 • 查看参考答案 o 1-9.如果二进制独立等概信号的码元宽度为 ,求 和 ;若改为四进制信号,码元宽 度不变,求传码率 和独立等概率时的传信率 。 • 查看参考答案

解:(1)已知码元宽度了=0.5m,则元速幸 品-号-20008 二讲时,信息速蜜等于码元速蜜,即 元==与=200(6站/) (2)若码元宽度不变,侧码元速率也不变,即仍为20006,故四进 制且独立等旧发送时,信息速率为 元=0g:4=2000×2=4000/ 1-10.已知某四进制数字传输系统的传信率为2400b5,接收端在0.5h内共收到216个错误码 元,试计算该系统的误码帝P。 ·查看参考答案 解:码元速率为 79 0.5内共传送的码元个数为 V=A,-1=1200x1800=2.16x10(个) 错误码元数N.216个,因此误码率.为 g-受w 第二章确知信号 本章主要内容: (1)信号和系统的分类 (2)能量信号和功率信号时域及频域分析 本章重点: 1.确知信号的频谱、频谱密度、能量谱密度和功率谱密度 2.确知信号的自相关函数和互相关函数 本章练习题: 2-1试证明图2-1中周期性信号的频谱为 4=(←1) s0.元22n+7os(2r+0m
o 1-10.已知某四进制数字传输系统的传信率为 2400 ,接收端在 0.5 内共收到 216 个错误码 元,试计算该系统的误码率 。 • 查看参考答案 o 第二章 确知信号 本章主要内容: (1)信号和系统的分类 (2)能量信号和功率信号时域及频域分析 本章重点: 1.确知信号的频谱、频谱密度、能量谱密度和功率谱密度 2.确知信号的自相关函数和互相关函数 本章练习题: 2-1 试证明图 2-1 中周期性信号的频谱为 =

0 2-1信号s()的波形 ·查看参考答案 证明:取区间-1/2::/2作为一个周明进行计算,并铃周期肛-2, 则由式(22-1)〔见教材)可得 cc070-倒 -金-awe的 点r 恤学去”学- 用=故-1 是2目 发月 将上式代入式(22-2(见拟材),得到 -c8.2产-+2“-- co-20a6网+元co5m-- 2-2设一个信号可以表示成 s()=2cos(2t+) -60<t<co 试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。 ·查看参考答案
• 查看参考答案 o 2-2 设一个信号可以表示成 试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。 • 查看参考答案

解:(1)它是宰信号, (2)计其其功率诺密度:信号的标需A2,基频∫,=1,周期 T6=1,先求此周其期信号的里叶的系数C由式子2.2-1) (见教材),得 C-克:0aw-262m-9r金 8-0.1±1. 或者写成 所似,仅当士1时,上式材不等于0,并且得出 J-1 nt1 于是 ef-1 n=t1 格上式代入式(2.248〔见数材),得到:()的掉诺密度 n-三FUnr---d0 2-3设有一信号如下: 试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。 ·查看参考答案 解:(1)计算此信号的能量: 9a.全-e1-8-0(有限值) 所似此信号是能显信号。 (2)计算其能量谱密度:首先计算其频诺密度 n-”金-a金2--rawg· -n0-- 所似 水7 能量诺恋度 pf-44rf 2-4试问下列函数中哪一些满足谱密度的性质: (1)6(f)+cos'2f
o 2-3 设有一信号如下: 试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。 • 查看参考答案 o 2-4 试问下列函数中哪一些满足谱密度的性质: (1)

(2)a+if-a) (3)pa-f乃 。查看参考答案 解:由式(2.2-4(见教材)P-中得 (1)-o2对 P--c- 1-5/正恤4时西 不满足功痒诺的性质。 (2)a+-a P-[ta-a(r-a-af4-L-aw-1- 不满足功宰谱密度的性质 (3)anp(a-) -4-rEcfq-c (上式最后一步利用积分公式:“金一去后) 2-5试求出0-Acs的自相关函数,并从其自相关函数求出其功幸. ·查看参考答案
(2) (3) • 查看参考答案 o 2-5 试求出 的自相关函数,并从其自相关函数求出其功率。 • 查看参考答案

解:对于周明功率信号,自相关函数的定义为 -20ta -g《:《四 所以有 -gt--2产co2mco2t-明 《5o2工ko2ax)co2r/5)-2r/x恤2m1- (5to2=A2知r-4r. a2m/手mex5 cem25动--专a受 其中,-2x/0… 平均功率为 0号 功率诺密度为 n-grr.号o u-1-- 。其中,了1z 2-6设信号s④的傅里叶变换为S()=sin1了,试求此信号的自相关函数R,9。 ·查看参考答案
o 2-6 设信号 的傅里叶变换为 ,试求此信号的自相关函数 。 •查看参考答案

解:由式〔22-25)〔见教材)可知,若今试中:1,则 s(-c( 所似,直接得知 a 由自相关函数定义式(23-1(见材),并参照图2-2,可以 写出 9-69r-在4 :8:0-Hs1 图2-2 2-7已知一信号0的自相关函数为 R)-÷e k=常数 ()试求其功率谱密度P,)和功率P 试画出R,⊙和P,)的曲线。 ·查看参考答案
o 2-7 已知一信号 的自相关函数为 常数 (1) 试求其功率谱密度 和功率 试画出 和 的曲线。 • 查看参考答案
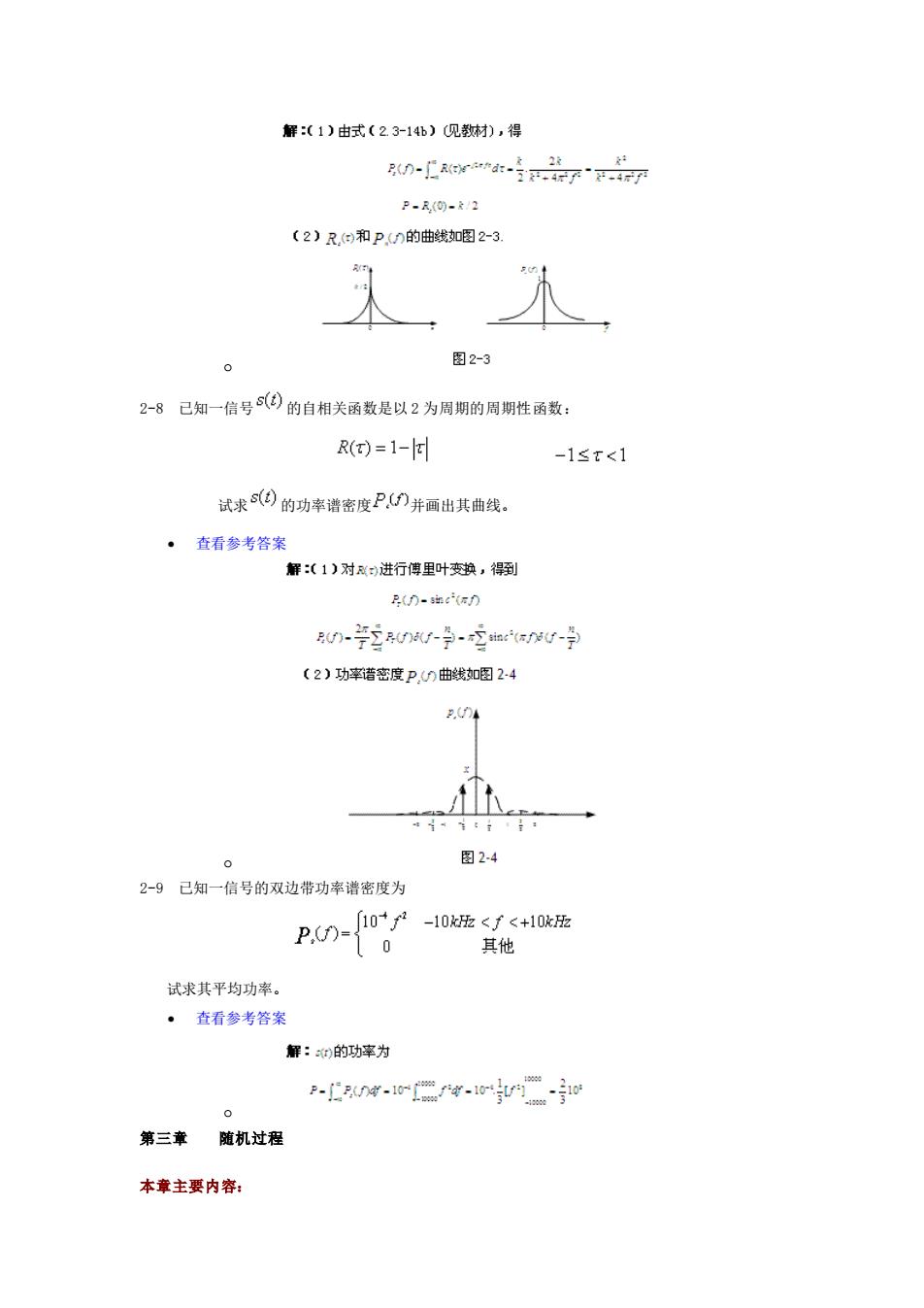
解(1)由式(2.3-14b)见教材),得 0-0i77 户-四-2 〔2)R,e和P(n的曲线如图2-3, 入人 图2-3 2-8已知一信号6()的自相关函数是以2为周期的周期性函数: R()=1- -1≤x<1 试求5(的功率谱密度P.并画出其曲线 ·查看参考答案 解(1)对进行停里叶变换,得到 2n-功 0n-20nr-9-恤r*sr-孕 〔2)功率谱密度P.曲线如图2-4 274 图24 2-9已知一信号的双边带功率谱密度为 ∫10+f2-10k<f<+10k p. 其他 试求其平均功率。 ·查看参考答案 解:的功率为 P-w1ryw1-o 第三章随机过程 本章主要内容:
o 2-8 已知一信号 的自相关函数是以 2 为周期的周期性函数: 试求 的功率谱密度 并画出其曲线。 • 查看参考答案 o 2-9 已知一信号的双边带功率谱密度为 试求其平均功率。 • 查看参考答案 o 第三章 随机过程 本章主要内容: