
M/G/1型排队系统
M/G/1型排队系统

Xidian Univ. M/G/A型排队系统 用户数不具有无后效性 。服务过程 6假定第个用户的服务时间为X,X是独立同分布的, 6与到达间隔相互独立。 令X={X1,X2,},则服务时间的均值和二阶矩为 平均服务时间=X=X)月 服务时间的二阶矩=X2=EX2} Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University M/G/1型排队系统 服务过程 假定第i个用户的服务时间为Xi,Xi是独立同分布的, 与到达间隔相互独立。 令 ,则服务时间的均值和二阶矩为 平均服务时间= = 服务时间的二阶矩= = X = {X1 , X 2 ,} X { } µ 1 E X = 2 X { }2 E X 用户数不具有无后效性

Xidian Univ. PK公式 ÷下面我们将证明,M/G/1排队系统的平均等待时间 为 AX2 W 21-p) 其中, p=么=双 该式称为P-K(Pollaczek-Khinchin)公式。 roadband Wireless communications caboratory.xidian university
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University 下面我们将证明,M/G/1排队系统的平均等待时间 为 其中, 该式称为P-K(Pollaczek-Khinchin)公式。 P-K公式 ( ρ) λ − = 2 1 2 X W λ X µ ρ = λ =

Xidian Univ. PK公式 。根据上述P-K公式,应用Little定理,可以得该系统的 平均时延为 7=灭+W=求+ 元X2 2(1-p) ÷平均队列长度为 2x2 No=iW= 21-p) ”系统中的平均用户数为 2x2 N=λT=λX+ 21-p) Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 根据上述P-K公式,应用Little定理,可以得该系统的 平均时延为 平均队列长度为 系统中的平均用户数为 ( ) 2 2 1 X T XW X λ ρ =+=+ − ( ρ) λ λ − = = 2 1 2 2 X N Q W ( ρ) λ λ λ − = = + 2 1 2 2 X N T X

Xidian Univ. PK公式 ÷如果G=M,即服务时间服从指数分布,M/M/1, X2= AX2 W三 2(1-p) 22(1-p)(1-p) 如果服务时间是常量,即M/D/1 等待时间是M/M/1 x=以 X2= 系统的一半 X W= 2(1-p) 22(1-p) 2μ(1-p) Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 如果G=M,即服务时间服从指数分布,M/M/1, 如果服务时间是常量,即M/D/1 2 2 2 µ X = µ X = 1 2 2 1 µ X = ( ) ( ) ( ) 2 2 2 1 21 21 1 X W λ ρ λ ρ µ ρµ ρ = = = − −− ( ) ( ) ( ) 2 2 1 1 21 21 2 1 X W λ ρ λ ρ µ ρ µρ = = = − −− 等待时间是M/M/1 系统的一半

Xidian Univ PK公式 P-K公式证明的思路是基于对平均剩余服务时间(Mean Residual Service Time)的求解。设第i个用户到达系统 时,第1个用户正在接受服务,其剩余服务时间为Ri,此 时等待队列中有i个用户, i-N, 服务员 第1个用户正在接受服务 第个用户 到达 N个用户 1正在接受服务 第个用户到达剩余服务时间R 等待服务 (a) () Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 P-K公式证明的思路是基于对平均剩余服务时间(Mean Residual Service Time)的求解。设第i个用户到达系统 时,第l个用户正在接受服务,其剩余服务时间为Ri,此 时等待队列中有Ni个用户

Xidian Univ. i-1…i-W 服务员 PK公式 第个用户 到达 N个用户 1正在接受服务 等待服务 设第k个用户的服务时间为X,则由图可知,用户的等待时间为 W=R,+N,个用户的服务时间=R+ k=i-N ·对上式求平均得 -ER)E x ER)+X.EN,} W=lim W;R=lim ER)No =E Ni) i-→00 W-R+XNo-R+-Ng-R+2W-R+pW W R 1-0 roadband Wireless communications caboratory.xidian university
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 设第k个用户的服务时间为Xk,则由图可知,用户i的等待时间为 对上式求平均得 i i W W →∞ = lim ∑ − = − = + = + i 1 k i N i i i i k i W R N 个用户的服务时间 R X { } { i} { i} i k i N Wi E Ri E X k E R X E N i = + • = + ∑ − = − 1 W R XN Q R N Q R λW R ρW µ µ = + = + = + = + 1 1 − ρ = 1 R W { i} i R E R →∞ = lim N Q = E{Ni}
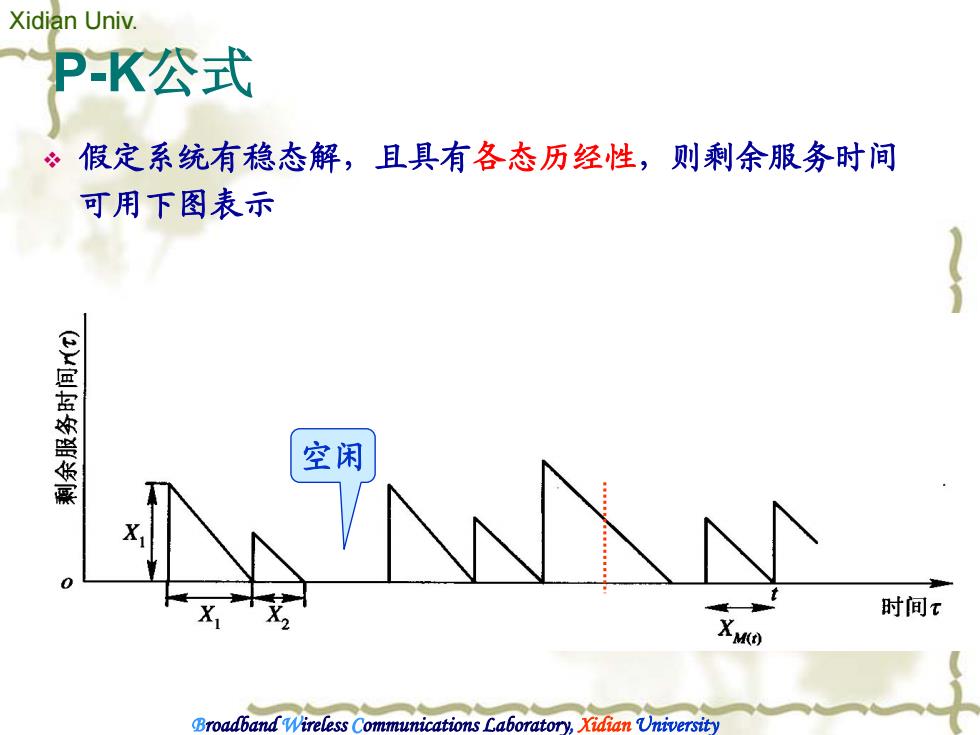
Xidian Univ. PK公式 ÷假定系统有稳态解,且具有各态历经性,则剩余服务时间 可用下图表示 空闲 时间t M Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 假定系统有稳态解,且具有各态历经性,则剩余服务时间 可用下图表示 空闲
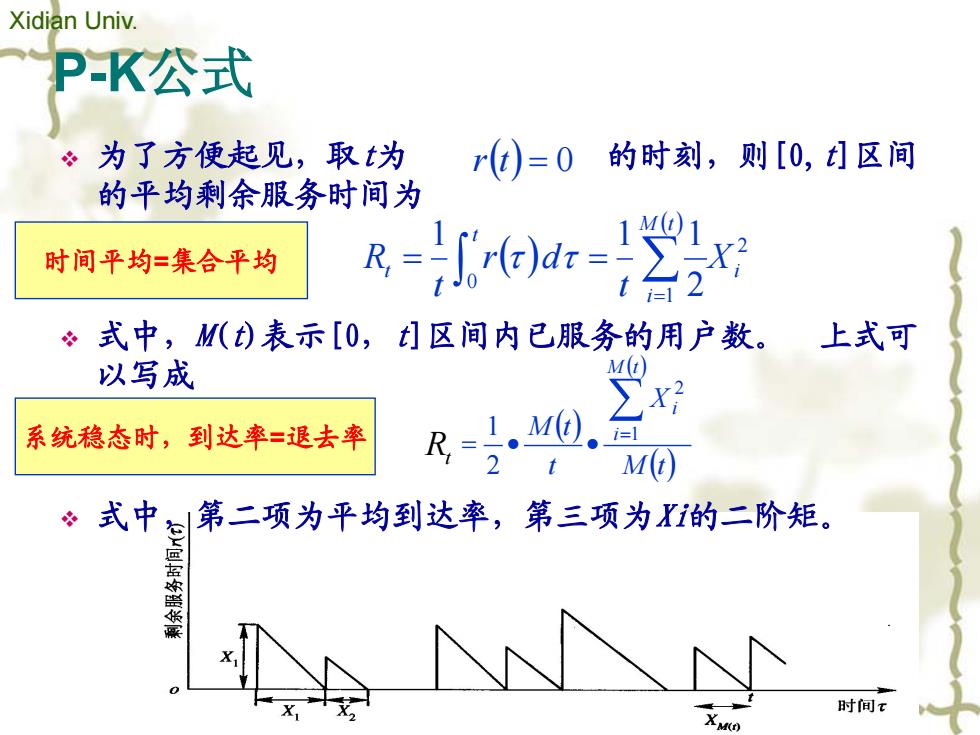
Xidian Univ. PK公式 为了方便起见,取为 rt)=0的时刻,则[0,t1区间 的平均剩余服务时间为 时间平均=集合平均 R=加2 式中,M()表示[0,t]区间内已服务的用户数。 上式可 以写成 M(t 系统稳态时,到达率=退去率 1 M( R,=2 i=1 M( 式中第二项为平均到达率,第三项为i的二阶矩。 时间x
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 为了方便起见,取t为 的时刻,则[0,t]区间 的平均剩余服务时间为 式中,M(t)表示[0,t]区间内已服务的用户数。 上式可 以写成 式中,第二项为平均到达率,第三项为Xi的二阶矩。 r(t) = 0 ( ) ( ) 2 1 0 2 1 1 1 i M t i t t X t r d t R ∫ ∑= = τ τ = ( ) ( ) M (t) X t M t R M t i i i ∑= = • • 1 2 2 1 时间平均=集合平均 系统稳态时,到达率=退去率 Rt

Xidian Univ. PK公式 g令t>0 ,得R=x R Ax2 W= Wax2 1-p 21-p) ÷即使P<1,如果X2o,则 W→0 。它说明,如果有少量用户有非常长的服务时间,一旦这些用 户被服务,将导致队列非常长。 Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University P-K公式 令 ,得 即使 ,如 果 ,则 它说明,如果有少量用户有非常长的服务时间,一旦这些用 户被服务,将导致队列非常长。 t → ∞ 2 2 1 R = λ X ( ρ) λ ρ − = − = 1 2 1 2 R X W 2 W ∝ X ρ < 1 → ∞ 2 X W → ∞