
Basic Queue Theory M/M/-/-Type Queues
Basic Queue Theory M/M/-/- Type Queues

Xidian Univ. Kendall's Notation for Queues *A/B/C/DE Shorthand notation where 4,B,C,D,E describe the queue Applicable to a large number of simple queueing scenarios Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University Kendall’s Notation for Queues A/B/C/D/E Shorthand notation where A, B, C, D, E describe the queue Applicable to a large number of simple queueing scenarios
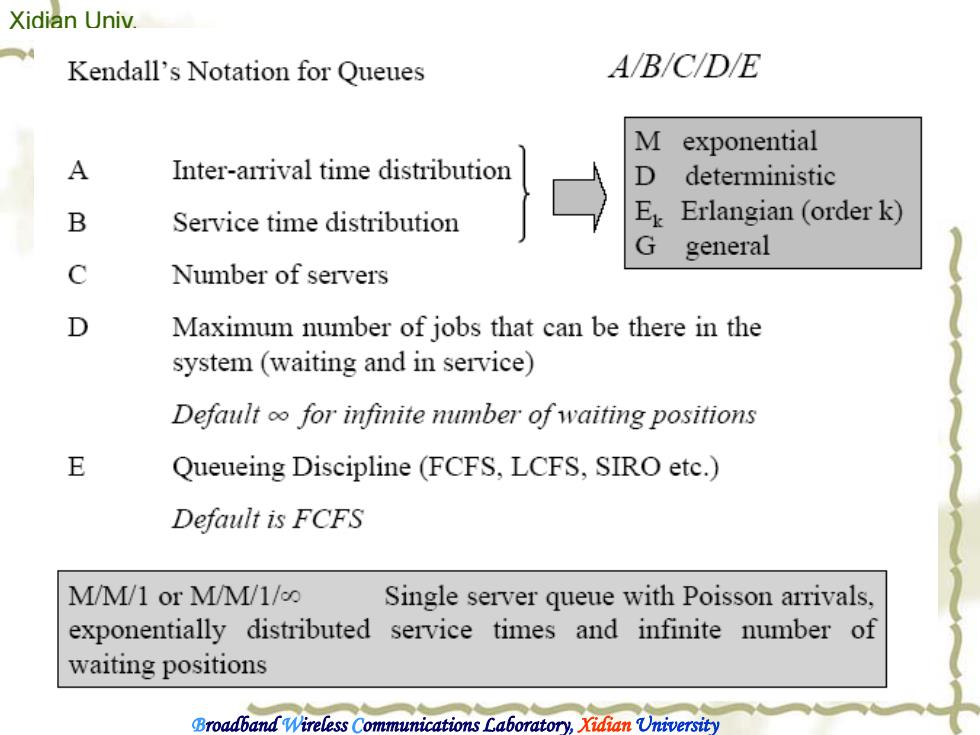
Xidian Univ Kendall's Notation for Queues AB/C/DE M exponential A Inter-arrival time distribution D deterministic B Service time distribution Erlangian (order k) G general C Number of servers D Maximum number of jobs that can be there in the system(waiting and in service) Default ofor infinite number of waiting positions E Queueing Discipline(FCFS,LCFS,SIRO etc.) Default is FCFS M/M/1orM/M/1/∞ Single server queue with Poisson arrivals, exponentially distributed service times and infinite number of waiting positions Broadband Wireless Communications Laboratory.Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University

Xidian Univ. M/M/m型排队系统 本课程将讨论“M/M/m”排队系统 6第一个字母表示到达过程的特征,M表示是无 记忆的Poisson过程。 6第二个字母表示服务时间的概率分布,M表示 指数分布,G表示一般分布,D表示确定性分布。 6第三个字母表示服务员的个数。有时还有第四 个字母,表示队列的长度。如果没有第四个字 母,则表示队列的长度无限大。 Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University M/M/m型排队系统 本课程将讨论“M/M/m”排队系统 第一个字母表示到达过程的特征,M表示是无 记忆的Poisson过程。 第二个字母表示服务时间的概率分布,M表示 指数分布,G表示一般分布,D表示确定性分布。 第三个字母表示服务员的个数。有时还有第四 个字母,表示队列的长度。如果没有第四个字 母,则表示队列的长度无限大

M/M/1排队系统
M/M/1排队系统

Xidian Univ. M/M/1排队系统 M/M/1排队系统的示意图如图所示。 到达过程为Poisson:过程,到达率为; ÷系统允许排队的队长可以是无限的(系统的缓存容量无限大); 。服务过程为指数过程,服务速率为山(平均服务时间为 服务员的数目为1,到达过程与服务过程相互独立。 无限容量队列 Poisson 到达过程 负指数 服务过程 Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University M/M/1排队系统 M/M/1排队系统的示意图如图所示。 到达过程为Poisson过程,到达率为λ; 系统允许排队的队长可以是无限的(系统的缓存容量无限大); 服务过程为指数过程,服务速率为µ(平均服务时间为 ), 服务员的数目为1,到达过程与服务过程相互独立。 µ 1 S 无限容量队列 Poisson 到达过程 负指数 服务过程

Xidian Univ. M/M/1排队系统 ÷我们将从四个方面对M/M/1排队系统的性能进行描 述: ó到达过程的统计特性 ó服务过程的统计特性 ó系统中的状态转移特性 ó系统的稳态分布 roadband Wireless communications caboratory.xidian university
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University M/M/1排队系统 我们将从四个方面对M/M/1排队系统的性能进行描 述: 到达过程的统计特性 服务过程的统计特性 系统中的状态转移特性 系统的稳态分布

Xidian Univ. 到达过程 。在M/M/1队列中,到达过程为Poiss0n过程 设一个随机过程为{A(),t≥0}的取值为非负整数,如果该 过程满足下列条件,则称该过程为到达率为入的Poisson(泊 松)过程。 6A(t)是一个计数过程,它表示在[0,t)区间内到达的用 户总数,A(0)=0,A(t)的状态空间为{0,1,2,.}。 -0 t-1tnt+1 图1-12 Poisson到达过程示意图 Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University 到达过程 在M/M/1队列中,到达过程为Poisson过程 设一个随机过程为{A(t),t≥0}的取值为非负整数,如果该 过程满足下列条件,则称该过程为到达率为λ的Poisson(泊 松)过程。 A(t)是一个计数过程,它表示在[0, t)区间内到达的用 户总数,A(0)=0,A(t)的状态空间为{0,1,2,…}

Xidian Univ 到达过程 6A(是一个独立增量过程。即在两个不同时间区间(区 间不重叠)内到达的用户数是相互独立的。 6任一个长度为τ的区间内,到达的用户数服从参数为工 的Poisson:分布,即 P(At+)-A0=m)=o”e 其均值和方差均为π。 由于在区间τ内平均到达的用户数为,则为单位时间 平均到达的用户数或称为到达率。 roadband Wireless communications caboratory.xidian university
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University 到达过程 A(t)是一个独立增量过程。即在两个不同时间区间(区 间 不重叠)内到达的用户数是相互独立的。 任一个长度为τ的区间内,到达的用户数服从参数为λτ 的Poisson分布,即 其均值和方差均为λτ 。 由于在区间τ内平均到达的用户数为λτ,则λ为单位时间 平均到达的用户数或称为到达率。 ( ( ( ) () ) n P At At n e n λτ) −λτ +τ − = = !

Xidian Univ. 到达过程 。Poisson:过程的基本特征有: 6到达时间间隔相互独立,且服从指数分布,其概率密度函 数为 Un tn+l -tn p(tn)=入ew 其分布函数为 P(t,0 顾客到达过程为到达率为入的Poisson:过程”与说“顾客 到达间隔相互独立且服从参数为入的指数分布”是等价的。 Broadband Wireless Communications Laboratory,Xidian University
Xidian Univ. Broadband Wireless Communications Laboratory, Xidian University 到达过程 Poisson过程的基本特征有: 到达时间间隔相互独立,且服从指数分布,其概率密度函 数为 其分布函数为 顾客到达过程为到达率为λ的Poisson过程”与说“顾客 到达间隔相互独立且服从参数为λ的指数分布”是等价的。 nn n 1 t t + τ= − ( ) n p e n −λτ τ =λ ( )1 0 s P s es n −λ τ