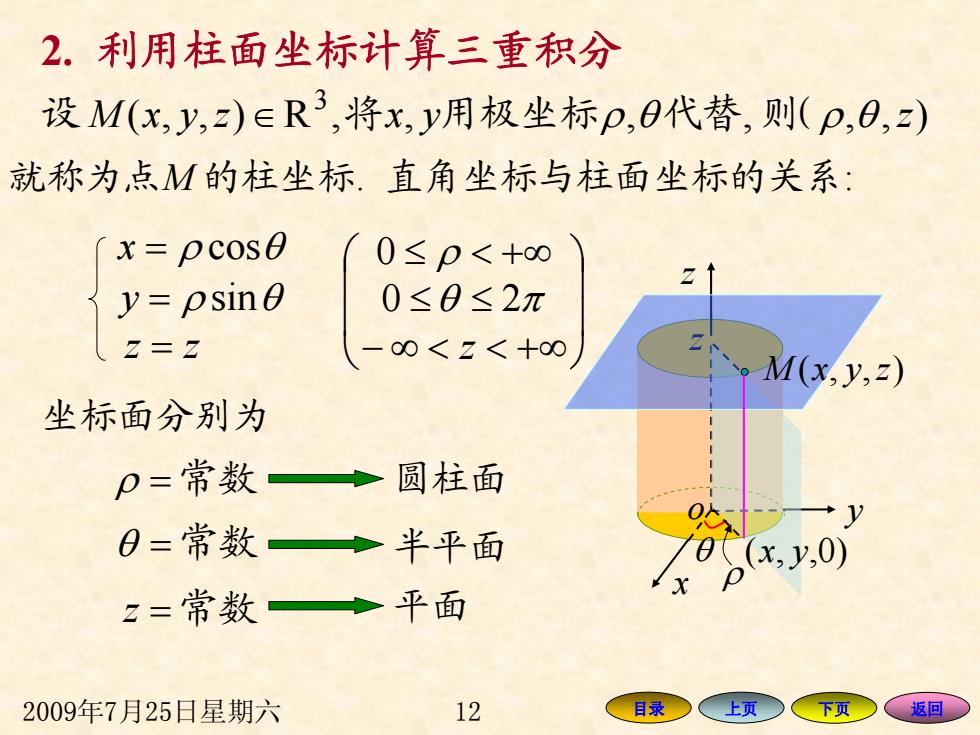
2.利用柱面坐标计算三重积分 设M(x,y,z)eR3,将x,y用极坐标p,0代替，则(p,0,z) 就称为，点M的柱坐标.直角坐标与柱面坐标的关系： x=pcose 0≤p<+∞ y=psine 0≤0≤2π z=z -00<z<十0 1M(x,y,2) 坐标面分别为 p=常数 圆柱面 0=常数◆半平面 z=常数 平面 2009年7月25日星期六 12 目录○ 上页 下页 返回 2009年7月25日星期六 12 目录 上页 下页 返回 o x y z ( , , ) R , 3 设 M x y z ∈ 将 x, y用极坐标 ρ,θ代替, 则 （ ρ,θ ,z ) 就称为点 M 的柱坐标. ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ∞ < < +∞ ≤ ≤ ≤ < + ∞ z θ π ρ 0 2 0 y = ρ sin θ z = z x = ρ cos θ 直角坐标与柱面坐标的关系: ρ = 常数 坐标面分别为 圆柱面 θ = 常数 半平面 z = 常数 平面 o θ z M ( x, y,z ) ρ ( x, y,0 ) 2. 利用柱面坐标计算三重积分