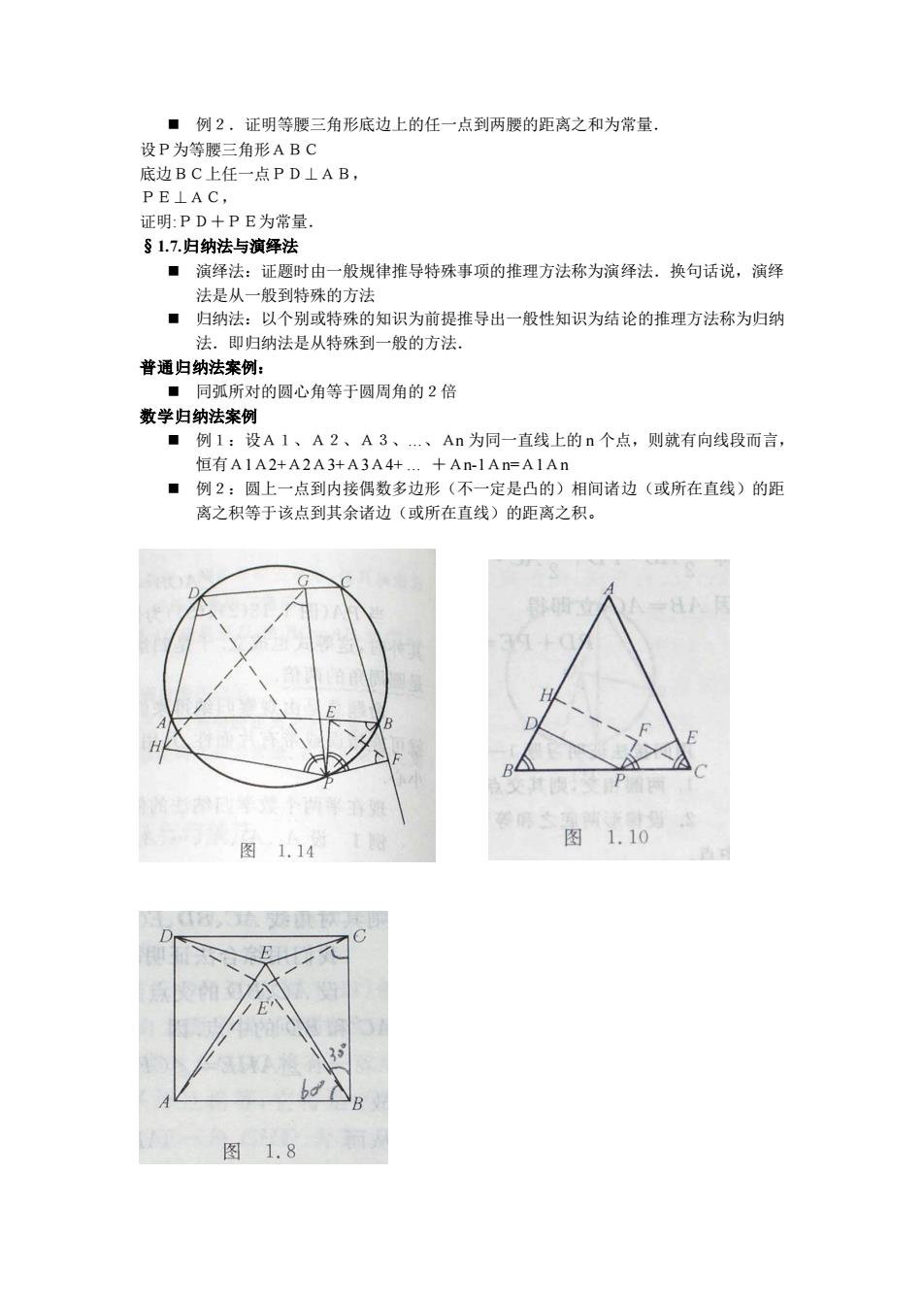
■例2.证明等腰三角形底边上的任一点到两腰的距离之和为常量. 设P为笔腰二角形ABC 证明：PD十PE为常量 §1.7.归纳法与演绎法 ■演绎法：证题时由一般规律推导特殊事项的推理方法称为演绎法，换句话说，演绎 法是从一般到特殊的方法 ■归纳法： 以个别或特殊的知识为前提推导出一般性知识为结论的推理方法称为归纳 法。即归纳法是从特殊到一般的方法。 普通归纳法案例： ■同弧所对的圆心角等于圆周角的2倍 数学归纳法案例 ■例1：设A1、A2、A3、An为同一直线上的n个点，则就有向线段而言 恒有A1A2+A2A3计A3A4++An-1An=A1An ■例2：圆上一点到内接偶数多边形（不一定是凸的）相间诸边（或所在直线）的距 离之积等于该点到其余诸边（或所在直线）的距离之积。 图1.10 图1.8 ◼ 例２．证明等腰三角形底边上的任一点到两腰的距离之和为常量． 设Ｐ为等腰三角形ＡＢＣ 底边ＢＣ上任一点ＰＤ⊥ＡＢ， ＰＥ⊥ＡＣ， 证明:ＰＤ＋ＰＥ为常量． §1.7.归纳法与演绎法 ◼ 演绎法：证题时由一般规律推导特殊事项的推理方法称为演绎法．换句话说，演绎 法是从一般到特殊的方法 ◼ 归纳法：以个别或特殊的知识为前提推导出一般性知识为结论的推理方法称为归纳 法．即归纳法是从特殊到一般的方法． 普通归纳法案例： ◼ 同弧所对的圆心角等于圆周角的２倍 数学归纳法案例 ◼ 例１：设Ａ１、Ａ２、Ａ３、.、Ａn 为同一直线上的 n 个点，则就有向线段而言， 恒有Ａ1Ａ2+Ａ2Ａ3+Ａ3Ａ4+ . ＋Ａn-1Ａn=Ａ1Ａn ◼ 例２：圆上一点到内接偶数多边形（不一定是凸的）相间诸边（或所在直线）的距 离之积等于该点到其余诸边（或所在直线）的距离之积