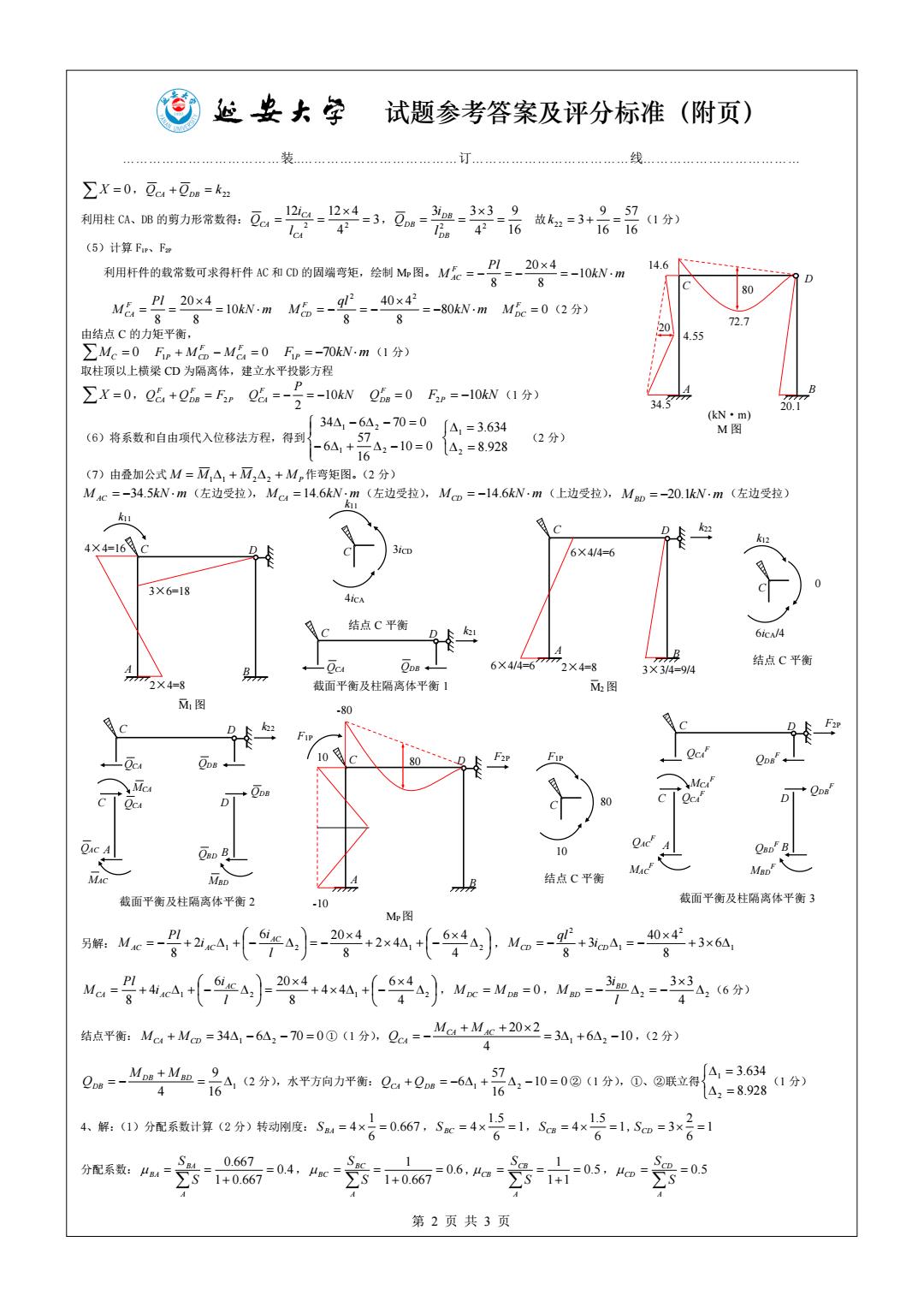
丝安大字 试题参考答案及评分标准（附页） 装 .订 线 ∑X=0,O+Os=k2 有阴胜0电的时力形常数得：0学学-3.O。一号-装3-名 6s4216 故k2=3+9=57 (1分) 1616 (5)计算Fp、Fm 用杆件的载常数可求符杆件AC和cD的固端弯矩，绘制0闲。M二-？=一X4 14.6 =-10kN.m 8 80 ==20x4=10N.mM6=-9头-40x Me=8 8 8 8 =-80kWmM5c=0(2分) 20 72.7 由结点C的力矩平衡， 4.55 ∑Me=0Fp+M-ME=0Fp=-70kW.m(1分) 取柱顶以上横梁CD为隔离体，建立水平投影方程 P ∑X=0.e%+0=F,C%=-2-10Nei=0Bm=-10kN1分) 34 201 34A1-6A2-70=0∫△1=3.634 (kN·m) (6)将系数和自由项代入位移法方程，得到 M图 57 -6a+i6a,-10=0a,=8928 (2分) (7)由叠加公式M=M△，+M2△2+M,作弯矩图。(2分) M4c=-34.5kW·m(左边受拉)，Mc1=14.6kW,m(左边受拉)，Mm=-14.6kWm(上边受拉)，Mo=-20.1kW.m(左边受拉) C D k2 4×4=16 D ICD 6×4/4=6 3×6=18 4icA C 结点C平衡 6ic/4 A 6X4/4=677 2X4=8 结点C平衡 3×3/4=9/4 72X4=8 截面平衡及柱隔离体平衡1 M2图 M1图 -80 ④C -0c B OC A 10 结点C平衡 截面平衡及柱隔离体平衡2 -10 截面平衡及柱隔离体平衡3 Mr图 -+3×6△ 8 Ma= +r4+(学4户=04(6a小M=a=0,Mo=-A=-36分 结点平衡：M+Mn=34-64,-70=00(1分.Qa=-M+M+20x2=34+6A,-10,2分 4 2地Ma+MeE942分，衣平方向力开衡：Qu+9s=-64+巴A,-10=0②1分@，②联立容A=36 4 16 4,=8.9281分) 4解.D分配系数计算2分)转动度：5=4×名-067，S=4× =1,5m=4x15 6 分配系数：4A= 0.667 1+0.667 =0.4,ac= 1+067-0.6,e 21=05, Sm=0.5 第2页共3页试题参考答案及评分标准（附页） ………………………………装..………………………………订………………………………线……………………………… 第 2 页 共 3 页 X = 0， 22 Q Q k CA + DB = 利用柱 CA、DB 的剪力形常数得： 3 4 12 12 4 2 2 =  = = CA CA CA l i Q ， 16 9 4 3 3 3 2 2 =  = = DB DB DB l i Q 故 16 57 16 9 k22 = 3 + = （1 分） （5）计算 F1P、F2P 利用杆件的载常数可求得杆件 AC 和 CD 的固端弯矩，绘制 MP图。 kN m Pl M F AC = −   = − = − 10 8 20 4 8 kN m Pl M F CA =   = = 10 8 20 4 8 k N m ql M F CD = −   = − = − 80 8 40 4 8 2 2 = 0 F M DC （2 分） 由结点 C 的力矩平衡， MC = 0 1 + − = 0 F CA F F P MCD M F1P = −70kNm （1 分） 取柱顶以上横梁 CD 为隔离体，建立水平投影方程 X = 0， P F DB F QCA + Q = F2 kN P Q F CA 10 2 = − = − = 0 F QDB F2P = −10kN （1 分） （6）将系数和自由项代入位移法方程，得到     −  +  − =  −  − = 10 0 16 57 6 34 6 70 0 1 2 1 2     =  = 8.928 3.634 2 1 （2 分） （7）由叠加公式 M = M11 + M22 + MP 作弯矩图。（2 分） M AC = −34.5kN  m （左边受拉）， MCA =14.6kN  m （左边受拉）， MCD = −14.6kN  m （上边受拉）， MBD = −20.1kNm （左边受拉） 另解：         +   + −   = −      = − + 1 + − 2 1 2 4 6 4 2 4 8 6 20 4 2 8 l i i Pl M AC AC AC ， 1 2 1 2 3 6 8 40 4 3 8 +    CD = − + iCD  = − ql M         +   + −   =      = + 1 + − 2 1 2 4 6 4 4 4 8 6 20 4 4 8 l i i Pl M AC CA AC ， M DC = M DB = 0 ， 2 2 4 3 3 3   = −  = − l i M BD BD （6 分） 结点平衡： MCA + MCD = 341 − 62 − 70 = 0 ①（1 分）， 3 6 10 4 20 2 = 1 + 2 − + +  = − CA AC CA M M Q ，（2 分） 1 16 9 4 =  + = − DB BD DB M M Q （2 分），水平方向力平衡： 10 0 16 57 QCA + QDB = −61 + 2 − = ②（1 分），①、②联立得     =  = 8.928 3.634 2 1 （1 分） 4、解：（1）分配系数计算（2 分）转动刚度： 0.667 6 1 S BA = 4 = ， 1 6 1.5 S BC = 4 = ， 1 6 1.5 SCB = 4 = , 1 6 2 SCD = 3 = 分配系数： 0.4 1 0.667 0.667 = + = =  A BA BA S S  ， 0.6 1 0.667 1 = + = =  A BC BC S S  , 0.5 1 1 1 = + = =  A CB CB S S  ， = = 0.5  A CD CD S S  k11 3iCD 4iCA C 结点 C 平衡 C D QCA QDB k21 截面平衡及柱隔离体平衡 1 C D A B 2×4=8 M2 图 6×4/4=6 6×4/4=6 3×3/4=9/4 k22 k12 0 6iCA/4 C 结点 C 平衡 C D A B 3×6=18 4×4=16 2×4=8 M1 图 k11 C D A B QCA QDB QCA MCA QAC C MAC k22 D QDB QBD MBD 截面平衡及柱隔离体平衡 2 C D A B -10 MP图 F2P F1P 10 -80 80 F1P 80 10 C 结点 C 平衡 C D A B QCA F QDB F MCA F C F2P D 截面平衡及柱隔离体平衡 3 QCA F QDB F QAC F MAC F QBD F MBD F C D A B 14.6 34.5 20.1 20 80 4.55 72.7 (kN·m) M 图